Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dordal, Peter Lars
1989.
Towers in [ω]ω and ωω.
Annals of Pure and Applied Logic,
Vol. 45,
Issue. 3,
p.
247.
Nyikos, Peter J.
1990.
On first countable, countably compact spaces II: remainders in a van Douwen construction and P-ideals.
Topology and its Applications,
Vol. 35,
Issue. 2-3,
p.
185.
Nyikos, Peter J.
1992.
Subsets of ωω and the Fréchet-Urysohn and αi-properties.
Topology and its Applications,
Vol. 48,
Issue. 2,
p.
91.
Balcar, Bohuslav
and
Simon, Petr
1995.
Baire number of the spaces of uniform ultrafilters.
Israel Journal of Mathematics,
Vol. 92,
Issue. 1-3,
p.
263.
Shelah, Saharon
Brendle, Jörg
and
Shelah, Saharon
1999.
Ultrafilters on 𝜔-their ideals and their cardinal characteristics.
Transactions of the American Mathematical Society,
Vol. 351,
Issue. 7,
p.
2643.
Tsaban, Boaz
2004.
The combinatorics of splittability.
Annals of Pure and Applied Logic,
Vol. 129,
Issue. 1-3,
p.
107.
Blass, Andreas
2010.
Handbook of Set Theory.
p.
395.
Halbeisen, Lorenz J.
2012.
Combinatorial Set Theory.
p.
179.
Balcar, Bohuslav
Doucha, Michal
and
Hrušák, Michael
2015.
Base Tree Property.
Order,
Vol. 32,
Issue. 1,
p.
69.
Dow, Alan
2020.
P-filters and Cohen, random, and Laver forcing.
Topology and its Applications,
Vol. 281,
Issue. ,
p.
107200.
Pawlikowski, Janusz
and
Stadnicki, Wojciech
2020.
Playing with Mathias.
Topology and its Applications,
Vol. 285,
Issue. ,
p.
107387.
Fischer, Vera
Koelbing, Marlene
and
Wohofsky, Wolfgang
2023.
Games on Base Matrices.
Notre Dame Journal of Formal Logic,
Vol. 64,
Issue. 2,
Fischer, Vera
Koelbing, Marlene
and
Wohofsky, Wolfgang
2024.
Refining systems of mad families.
Israel Journal of Mathematics,
Vol. 262,
Issue. 1,
p.
191.

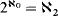 , and in which there are no
, and in which there are no 