No CrossRef data available.
Article contents
Model theory under the axiom of determinateness
Published online by Cambridge University Press: 12 March 2014
Abstract
We initiate the study of model theory in the absence of the Axiom of Choice, using the Axiom of Determinateness as a powerful substitute. We first show that, in this context, 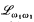 is no more powerful than first-order logic. The emphasis then turns to upward Löwenhein-Skolem theorems; ℵ1 is the Hanf number of first-order logic, of
is no more powerful than first-order logic. The emphasis then turns to upward Löwenhein-Skolem theorems; ℵ1 is the Hanf number of first-order logic, of 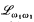 , and of a strong fragment of
, and of a strong fragment of 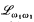 , The main technical innovation is the development of iterated ultrapowers using infinite supports; this requires an application of infinite-exponent partition relations. All our theorems can be proven from hypotheses weaker than AD.
, The main technical innovation is the development of iterated ultrapowers using infinite supports; this requires an application of infinite-exponent partition relations. All our theorems can be proven from hypotheses weaker than AD.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1985
References
REFERENCES
[2]Henle, J. M., Researches into the world of κ → (κ)κ, Annals of Mathematical Logic, vol. 17 (1979), pp. 151–169.CrossRefGoogle Scholar
[3]Kechris, A. S., The axiom of determinacy implies dependent choices in L(R), this Journal, vol. 49 (1984), pp. 161–173.Google Scholar
[4]Kechris, A. S., Kleinberg, E. M., Moschovakis, Y. N. and Woodin, W. H., The axiom of determinacy, strong partition properties, and nonsingular measures, Cabal Seminar 77–79 (Kechris, A. S., Martin, D. A. and Moschovakis, Y. N., editors), Lecture Notes in Mathematics, vol. 839, Springer-Verlag, Berlin, 1981, pp. 75–99.CrossRefGoogle Scholar
[5]Kechris, A. S. and Moschovakis, Y. N. (editors), Cabal Seminar 76–77, Lecture Notes in Mathematics, vol. 689, Springer-Verlag, Berlin, 1978.CrossRefGoogle Scholar
[6]Kleinberg, E. M., Infinitary combinatorics and the axiom of determinateness, Lecture Notes in Mathematics, vol. 612, Springer-Verlag, Berlin, 1977.CrossRefGoogle Scholar
[7]Solovay, R. M., A model for set theory in which every set of reals is Lebesgue measurable, Annals of Mathematics, ser. 2, vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar

