Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-30T23:36:30.127Z Has data issue: false hasContentIssue false
  • English
  • Français

MORE ON THE PRESERVATION OF LARGE CARDINALS UNDER CLASS FORCING

Part of: Set theory

Published online by Cambridge University Press:  13 September 2021

JOAN BAGARIA Open the ORCID record for JOAN BAGARIA [Opens in a new window]  and
ALEJANDRO POVEDA
JOAN BAGARIA
Affiliation:
INSTITUCIÓ CATALANA DE RECERCA I ESTUDIS AVANÇATS (ICREA) BARCELONA, SPAIN and DEPARTAMENT DE MATEMÀTIQUES I INFORMÀTICA UNIVERSITAT DE BARCELONA, GRAN VIA DE LES CORTS CATALANES BARCELONA 585, 08007, SPAIN E-mail: joan.bagaria@icrea.cat
ALEJANDRO POVEDA*
Affiliation:
DEPARTAMENT DE MATEMÀTIQUES I INFORMÀTICA UNIVERSITAT DE BARCELONA, GRAN VIA DE LES CORTS CATALANES BARCELONA 585, 08007, SPAIN Current address: EINSTEIN INSTITUTE OF MATHEMATICS HEBREW UNIVERSITY OF JERUSALEM JERUSALEM 91904, ISRAEL
*
E-mail: alejandro.poveda@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove two general results about the preservation of extendible and 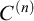$C^{(n)}$-extendible cardinals under a wide class of forcing iterations (Theorems 5.4 and 7.5). As applications we give new proofs of the preservation of Vopěnka’s Principle and 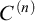$C^{(n)}$-extendible cardinals under Jensen’s iteration for forcing the GCH [17], previously obtained in [8, 27], respectively. We prove that 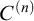$C^{(n)}$-extendible cardinals are preserved by forcing with standard Easton-support iterations for any possible 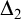$\Delta _2$-definable behaviour of the power-set function on regular cardinals. We show that one can force proper class-many disagreements between the universe and HOD with respect to the calculation of successors of regular cardinals, while preserving 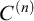$C^{(n)}$-extendible cardinals. We also show, assuming the GCH, that the class forcing iteration of Cummings–Foreman–Magidor for forcing 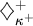$\diamondsuit _{\kappa ^+}^+$ at every 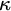$\kappa $ [10] preserves 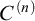$C^{(n)}$-extendible cardinals. We give an optimal result on the consistency of weak square principles and 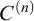$C^{(n)}$-extendible cardinals. In the last section prove another preservation result for 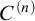$C^{(n)}$-extendible cardinals under very general (not necessarily definable or weakly homogeneous) class forcing iterations. As applications we prove the consistency of 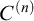$C^{(n)}$-extendible cardinals with 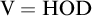$\mathrm {{V}}=\mathrm {{HOD}}$, and also with 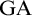$\mathrm {GA}$ (the Ground Axiom) plus 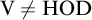$\mathrm {V}\neq \mathrm {HOD}$, the latter being a strengthening of a result from [14].

Keywords

large cardinalsclass forcing iterationsextendible cardinalsVopěnka’s Principle

MSC classification

Secondary: 03E35: Consistency and independence results 03E55: Large cardinals

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 1 , March 2023 , pp. 290 - 323
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bagaria, J., C (n)-cardinals . Archive for Mathematical Logic , vol. 51 (2012), no. 3, pp. 213–240.CrossRefGoogle Scholar
Bagaria, J., Casacuberta, C., Mathias, A. R. D., and Rosickỳ, J.. Definable orthogonality classes in accessible categories are small . Journal of the European Mathematical Society , vol. 17 (2015), no. 3, pp. 549–589.CrossRefGoogle Scholar
Bagaria, J., Gitman, V., and Schindler, R., Generic Vopěnka’s principle, remarkable cardinals, and the weak proper forcing Axiom . Archive for Mathematical Logic , vol. 56 (2017), nos. 1–2, pp. 1–20.CrossRefGoogle Scholar
Bagaria, J., Hamkins, J. D., Tsaprounis, K., and Usuba, T., Superstrong and other large cardinals are never Laver indestructible . Archive for Mathematical Logic , vol. 55 (2016), nos. 1–2, pp. 19–35.CrossRefGoogle Scholar
Bagaria, J. and Magidor, M., On ${\omega}_1$ -strongly compact cardinals, this Journal, vol. 79 (2014), no. 1, pp. 266–278.Google Scholar
Boney, W., Model theoretic characterizations of large cardinals. Israel Journal of Mathematics , vol. 236 (2020), pp. 133–181.CrossRefGoogle Scholar
Brooke-Taylor, A. D., Large cardinals and definable well-orders on the universe, this Journal, vol. 74 (2009), no. 2, pp. 641–654.Google Scholar
Brooke-Taylor, A. D., Indestructibility of Vopěnka’s principle . Archive for Mathematical Logic , vol. 50 (2011), no. 5, pp. 515–529.CrossRefGoogle Scholar
Brooke-Taylor, A. D. and Friedman, S.-D., Subcompact cardinals, squares, and stationary reflection . Israel Journal of Mathematics , vol. 197 (2013), no. 1, pp. 453–473.CrossRefGoogle Scholar
Cummings, J., Foreman, M., and Magidor, M., Squares, scales and stationary reflection . Journal of Mathematical Logic , vol. 1 (2001), no. 1, pp. 35–98.CrossRefGoogle Scholar
Dobrinen, N. and Friedman, S.-D., Homogeneous iteration and measure one covering relative to HOD . Archive for Mathematical Logic , vol. 47 (2008), no. 7, pp. 711–718.CrossRefGoogle Scholar
Friedman, S.-D., Fine Structure and Class Forcing , Walter de Gruyter, Berlin, 2000.CrossRefGoogle Scholar
Gitik, M. and Shelah, S., On certain indestructibility of strong cardinals and a question of Hajnal . Archive for Mathematical Logic , vol. 28 (1989), no. 1, pp. 35–42.CrossRefGoogle Scholar
Hamkins, J., Reitz, J., and Woodin, W. H., The ground axiom is consistent with V $\,\ne\,$ HOD . Proceedings of the American Mathematical Society , vol. 136 (2008), no. 8, pp. 2943–2949.CrossRefGoogle Scholar
Hamkins, J. D., The lottery preparation . Annals of Pure and Applied Logic , vol. 101 (2000), nos. 2–3, pp. 103–146.CrossRefGoogle Scholar
Jech, T., Set Theory: The Third Millennium Edition, Revised and Expanded , Springer Monographs in Mathematics, vol. 14, Springer, Berlin, 2002.Google Scholar
Jensen, R. B., Measurable cardinals and the GCH , Axiomatic Set Theory (T. J. Jech, editor), Proceedings of Symposia in Pure Mathematics, vol. 13, American Mathematical Society, Providence, RI, 1974, pp. 175–178.CrossRefGoogle Scholar
Kanamori, A., The Higher Infinite , Springer Monographs in Mathematics, Springer, Berlin, 2003.Google Scholar
Laver, R., Making the supercompactness of $\kappa$ indestructible under $\kappa$ -directed closed forcing . Israel Journal of Mathematics , vol. 29 (1978), no. 4, pp. 385–388.CrossRefGoogle Scholar
Lücke, P., Njegomir, A., Holy, P., Krapf, R., and Schlicht, P., Class forcing, the forcing theorem and Boolean completions, this Journal, vol. 81 (2016), no. 4, pp. 1500–1530.Google Scholar
Magidor, M., On the role of supercompact and extendible cardinals in logic . Israel Journal of Mathematics , vol. 10 (1971), no. 2, pp. 147–157.CrossRefGoogle Scholar
McAloon, K., Consistency results about ordinal definability . Annals of Mathematical Logic , vol. 2 (1971), no. 4, pp. 449–467.CrossRefGoogle Scholar
Reitz, J., The ground Axiom , Ph.D. thesis, The Graduate Center of the City University of New York, 2006.Google Scholar
Schimmerling, E., Combinatorial principles in the core model for one Woodin cardinal . Annals of Pure and Applied Logic , vol. 74 (1995), no. 2, pp. 153–201.CrossRefGoogle Scholar
Solovay, R. M., Strongly compact cardinals and the GCH , Proceedings of the Tarski Symposium , (L. Henkin, J. Addison, C. C. Chang, W. Craig, D. Scott, and R. Vaught, editors) Proceedings of Symposia in Pure Mathematics, vol. 25, American Mathematical Society, Providence, RI, 1974, pp. 365–372.CrossRefGoogle Scholar
Tsaprounis, K., Large cardinals and resurrection axioms , Ph.D. thesis, Universitat de Barcelona, 2012.Google Scholar
Tsaprounis, K., On extendible cardinals and the GCH . Archive for Mathematical Logic , vol. 52 (2013), nos. 5–6, pp. 593–602.CrossRefGoogle Scholar
Tsaprounis, K., On ${C}^{(n)}$ -extendible cardinals, this Journal, vol. 83 (2018), pp. 1112–1131.Google Scholar
Woodin, W. H., Suitable extender models I . Journal of Mathematical Logic , vol. 10 (2010), no. 01n02, pp. 101–339.CrossRefGoogle Scholar