No CrossRef data available.
Article contents
MORE ZFC INEQUALITIES BETWEEN CARDINAL INVARIANTS
Published online by Cambridge University Press: 02 August 2021
Abstract
Motivated by recent results and questions of Raghavan and Shelah, we present ZFC theorems on the bounding and various almost disjointness numbers, as well as on reaping and dominating families on uncountable, regular cardinals. We show that if 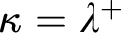 $\kappa =\lambda ^+$ for some
$\kappa =\lambda ^+$ for some 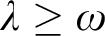 $\lambda \geq \omega $ and
$\lambda \geq \omega $ and 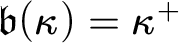 $\mathfrak {b}(\kappa )=\kappa ^+$ then
$\mathfrak {b}(\kappa )=\kappa ^+$ then 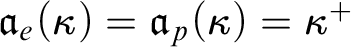 $\mathfrak {a}_e(\kappa )=\mathfrak {a}_p(\kappa )=\kappa ^+$. If, additionally,
$\mathfrak {a}_e(\kappa )=\mathfrak {a}_p(\kappa )=\kappa ^+$. If, additionally, 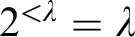 $2^{<\lambda }=\lambda $ then
$2^{<\lambda }=\lambda $ then 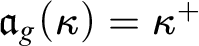 $\mathfrak {a}_g(\kappa )=\kappa ^+$ as well. Furthermore, we prove a variety of new bounds for
$\mathfrak {a}_g(\kappa )=\kappa ^+$ as well. Furthermore, we prove a variety of new bounds for 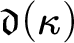 $\mathfrak {d}(\kappa )$ in terms of
$\mathfrak {d}(\kappa )$ in terms of 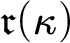 $\mathfrak {r}(\kappa )$, including
$\mathfrak {r}(\kappa )$, including 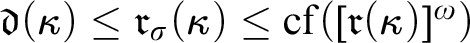 $\mathfrak {d}(\kappa )\leq \mathfrak {r}_\sigma (\kappa )\leq \operatorname {\mathrm {cf}}([\mathfrak {r}(\kappa )]^\omega )$, and
$\mathfrak {d}(\kappa )\leq \mathfrak {r}_\sigma (\kappa )\leq \operatorname {\mathrm {cf}}([\mathfrak {r}(\kappa )]^\omega )$, and 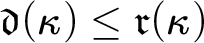 $\mathfrak {d}(\kappa )\leq \mathfrak {r}(\kappa )$ whenever
$\mathfrak {d}(\kappa )\leq \mathfrak {r}(\kappa )$ whenever 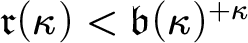 $\mathfrak {r}(\kappa )<\mathfrak {b}(\kappa )^{+\kappa }$ or
$\mathfrak {r}(\kappa )<\mathfrak {b}(\kappa )^{+\kappa }$ or 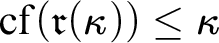 $\operatorname {\mathrm {cf}}(\mathfrak {r}(\kappa ))\leq \kappa $ holds.
$\operatorname {\mathrm {cf}}(\mathfrak {r}(\kappa ))\leq \kappa $ holds.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Association for Symbolic Logic 2021


