Hostname: page-component-784d4fb959-jtjl6 Total loading time: 0 Render date: 2025-07-17T00:29:53.427Z Has data issue: false hasContentIssue false
  • English
  • Français

THE NEAT EMBEDDING PROBLEM FOR ALGEBRAS OTHER THAN CYLINDRIC ALGEBRASAND FOR INFINITE DIMENSIONS

Published online by Cambridge University Press:  17 April 2014

ROBIN HIRSCH  and
TAREK SAYED AHMED
ROBIN HIRSCH
Affiliation:
DEPARTMENT OF COMPUTER SCIENCE, UNIVERSITY COLLEGE LONDON, GOWER STREET LONDON, WC1E 6BT, UK E-mail: ucacrdh@live.ucl.ac.uk
TAREK SAYED AHMED
Affiliation:
DEPARTMENT OF MATHEMATICS, FACULTY OF SCIENCE, CAIRO UNIVERSITY, GIZA, EGYPT E-mail: e-mail: rutahmed@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Hirsch and Hodkinson proved, for 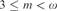$3 \le m < \omega $ and any 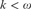$k < \omega $, that the class 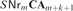$SNr_m {\bf{CA}}_{m + k + 1} $ is strictly contained in 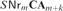$SNr_m {\bf{CA}}_{m + k} $ and if 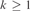$k \ge 1$ then the former class cannot be defined by any finite set offirst-order formulas, within the latter class. We generalize this result to thefollowing algebras of m-ary relations for which the neat reductoperator 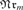$_m $ is meaningful: polyadic algebras with or without equality andsubstitution algebras. We also generalize this result to allow the case wherem is an infinite ordinal, using quasipolyadic algebras inplace of polyadic algebras (with or without equality).

Keywords

03G1503C10.Algebraic logic. cylindric algebras. quasi-polyadic algebras. substitutionalgebrasneat reductsneat embeddings

Information

Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 1 , March 2014 , pp. 208 - 222
Copyright
Copyright © Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Ahmed, T. Sayed and Samir, B., A neat embedding theorem for expansions of cylindric algebras. Logic Journal of IGPL, vol. 15 (2007), pp. 41–51.Google Scholar
Andréka, H., Givant, S., Mikulás, S., Németi, I., and Simon, A., Notions of density that imply representability in algebraic logic. Annals of Pure and Applied Logic, vol. 91 (1998), pp. 93–190.Google Scholar
Daigneault, A. and Monk, J., Representation theory for polyadic algebras. Fundamenta Mathematicae, vol. 52 (1963), pp. 151–176.Google Scholar
Henkin, L., Monk, J., and Tarski, A., Cylindric algebras. Part I, North-Holland, Amsterdam, 1971.Google Scholar
Henkin, L., Monk, J., and Tarski, A., Cylindric algebras. Part II, North-Holland, Amsterdam, 1985.Google Scholar
Hirsch, R. and Hodkinson, I., Relation algebras from cylindric algebras, I. Annals of Pure and Applied Logic, vol. 112 (2001), pp. 225–266.Google Scholar
Hirsch, R. and Hodkinson, I., Relation algebras from cylindric algebras, II. Annals of Pure and Applied Logic, vol. 112 (2001), pp. 267–297.Google Scholar
Hirsch, R. and Hodkinson, I., Relation algebras by games, North-Holland, Elsevier Science, Amsterdam, 2002.Google Scholar
Hirsch, R., Hodkinson, I., and Maddux, R., Provability with finitely many variables. Bulletin of Symbolic Logic, vol. 8 (2002), no. 3, p. 353.Google Scholar
Hirsch, R., Hodkinson, I., and Maddux, R., Relation algebra reducts of cylindric algebras and an application to proof theory, this Journal, vol. 67 (2002), no. 1, pp. 197–213.Google Scholar
Németi, I., The class of neat reducts is not a variety but is closed w.r.t HP. Notre Dame Journal of Formal Logic, vol. 24 (1983), pp. 399–409.Google Scholar
Németi, I., Algebraisations of quantifier logics, an introductory overview. Studia Logica, vol. 50 (1991), no. 3/4, pp. 485–570. An extended version of this paper is available at http:/math-inst.hu pub algebraic-logic survey.dvi.Google Scholar
Pinter, C., A simple algebra of first order logic. Notre Dame Journal of Formal Logic, vol. 1 (1973), pp. 361–366.Google Scholar
Sain, I. and Thompson, R., Strictly finite schema axiomatization of quasi-polyadic algebras. Algebraic Logic (Andréka, H, Monk, J, and émeti, I N, editors), Colloq. Math. Soc. J. Bolyai, vol. 54, North-Holland, Amsterdam, 1991, pp. 539–571.Google Scholar