Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-11T20:27:11.868Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary use of 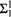induction in a reversal

Published online by Cambridge University Press:  12 March 2014

Itay Neeman
Itay Neeman*
Affiliation:
Department of Mathematics, University of California Los Angeles, Los Angeles, CA 90095-1555, USA, E-mail: ineeman@math.ucla.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Jullien's indecomposability theorem (INDEC) states that if a scattered countable linear order is indecomposable, then it is either indecomposable to the left, or indecomposable to the right. The theorem was shown by Montalbán to be a theorem of hyperarithmetic analysis, and then, in the base system RCA0 plus 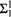induction, it was shown by Neeman to have strength strictly between weak 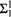choice and 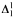comprehension. We prove in this paper that 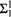induction is needed for the reversal of INDEC. that is for the proof that INDEC implies weak 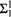choice. This is in contrast with the typical situation in reverse mathematics, where reversals can usually be refined to use only 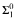induction.

Keywords

Reverse Mathematicsinductionweak choicelinear orderingsscatteredindecomposable
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 2 , June 2011 , pp. 561 - 574
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Hirschfeldt, Denis R. and Shore, Richard A., Combinatorial principles weaker than Ramsey's theorem for pairs, this Journal, vol. 72 (2007), no. 1, pp. 171–206.Google Scholar
[2]Jullien, Pierre, Contribution à l'étude des types d'ordre dispersés, Ph.D. thesis, Marseille, 1969.Google Scholar
[3]Medsalem, Medyahya Ould and Tanaka, Kazuyuki, -determinacy, comprehension and induction, this Journal, vol. 72 (2007), no. 2, pp. 452–462.Google Scholar
[4]Montalbán, Antonio, Indecomposable linear orderings and hyperarithmetic analysis, Journal of Mathematical Logic, vol. 6 (2006), no. 1, pp. 89–120.CrossRefGoogle Scholar
[5]Montalbán, Antonio, On the equimorphism types of linear orderings, The Bulletin of Symbolic Logic, vol. 13 (2007), no. 1, pp. 71–99.CrossRefGoogle Scholar
[6]Neeman, Itay, The strength of Jullien's indecomposability theorem, Journal of Mathematical Logic, vol. 8 (2009), no. 1, pp. 93–119.CrossRefGoogle Scholar
[7]Nemoto, Takako, Determinacy of Wadge classes and subsystems of second order arithmetic, Mathematical Logic Quarterly, vol. 55 (2009), no. 2, pp. 154–176.CrossRefGoogle Scholar
[8]Simpson, Stephen G., and transfinite induction, Logic Colloquium '80(Prague, 1980), Studies in Logic and the Foundations of Mathematics, vol. 108, North-Holland, Amsterdam, 1982, pp. 239–253.Google Scholar
[9]Simpson, Stephen G., Subsystems of second order arithmetic, second ed., Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
[10]Steel, John R., Determinateness and subsystems of analysis, Ph.D. thesis, University of California, Berkeley, 1977.Google Scholar
[11]Steel, John R., Forcing with tagged trees, Annals of Mathematical Logic, vol. 15 (1978), no. 1, pp. 55–74.CrossRefGoogle Scholar
[12]Wesep, Robert Van, Subsystems of second-order arithmetic, and descriptive set theory under the axiom of determinateness, Ph.D. thesis, University of California, Berkeley, 1977.Google Scholar