Article contents
A new theory of element and number1
Published online by Cambridge University Press: 12 March 2014
Extract
Quine remarked that the system of his book exclusive of *200 is a completely safe basal logic. Axioms of this basal logic are given by *100-*105 and *201-*202 in the book. For relation theory and number theory, we need some further axioms to guarantee elementhood of certain entities. In the article, Quine proposed to adopt as axioms f610 and the following two statements:
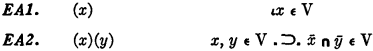
Information
- Type
- Articles
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1948
Footnotes
Throughout this paper, Quine's Mathematical logic (V 163) and his article Element and number (VII 121) will be referred to as the book and the article respectively.
References
3 This mutual deducibility was pointed out to me by Professor Quine, who also made many other very helpful criticisms and suggestions. I am also indebted to him for his kind encouragement.
4 It seems that we might, without using the powers of relations, have defined the matrix ‘x N y’ as follows:
But it is difficult to derive the desired theorems with this definition.
5 At first, I defined ‘x < y’ as ‘x ε Nn ▪ (⋆Є | Є) (x, y)’. The present version D41 is G. D. W. Berry's. He points out that, under my former definition, the theorems †665–667 are in themselves consistent with there being only a finite number of natural numbers plus one object y not a natural number but such that (x) (x ε Nn ▪ ⊃. x < y)
I am also indebted to Berry for numerous less striking corrections and suggestions.
6 We might have reduced all the defined symbols in our axioms to statement connectives and quantifiers plus ‘ε’, and merely set down formal truth-conditions for the schema ![]() in terms of our arithmetical model—thereby indicating the consistency of our rather weak axioms.
in terms of our arithmetical model—thereby indicating the consistency of our rather weak axioms.
- 4
- Cited by

