Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T19:26:38.214Z Has data issue: false hasContentIssue false
  • English
  • Français

A new version of Beth semantics for intuitionistic logic

Published online by Cambridge University Press:  12 March 2014

Dov M. Gabbay
Dov M. Gabbay*
Affiliation:
Bar-Ilan University, Ramat-Gan, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

We use the notation of Kripke's paper [1]. Let M = (G, K, R) be a tree structure and D a domain and η a Beth model on M. The truth conditions of the Beth semantics for ∨ and ∃ are (see [1]):

(a) η (A ∨ B, H) = T iff for some B ⊆ K, B bars H and for each H′ ∈ B, either η(A, H′) = T or η(B, H′) = T.

(b) η(∃xA(x), H) = T iff for some B ⊆ K, B bars H and for each H′ ∈ B there exists an a ∈ D such that η(A (a), H′) = T.

Suppose we change the truth definition η to η* by replacing condition (b) by the condition (b*) (well known from the Kripke interpretation):

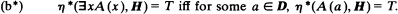
Call this type of interpretation the new version of Beth semantics. We prove

Theorem 1. Intuitionistic predicate logic is complete for the new version of the Beth semantics.

Since Beth structures are of constant domains, and in the new version of Beth semantics the truth conditions for ∧, →, ∃, ∀, ¬ are the same as for the Kripke interpretation, we get:

Corollary 2. The fragment without disjunction of the logic CD of constant domains (i.e. with the additional schema ∀x(A ∨ B(x))→ A ∨ ∀xB(x), x not free in A) equals the fragment without disjunction of intuitionistice logic.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 2 , June 1977 , pp. 306 - 308
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Kripke, S., Semantical analysis for intuitionistic logic. I, Formal systems and recursive functions (Crossley, J. and Dummett, M., Editors), North-Holland, Amsterdam, 1965.Google Scholar
[2]Fitting, M., Intuitionistic logic model theory and forcing, North-Holland, Amsterdam, 1969.Google Scholar
[3]Gabbay, D., Applications of trees to intermediate logics, this Journal, vol. 37 (1972), pp. 135–138.Google Scholar
[4]Görnemann, S., A logic stronger than intuitionism, this Journal, vol. 36 (1971), pp. 249–261.Google Scholar
[5]Gabbay, D., Semantical investigations in Heyting's predicate logic, D. Reidel (in press).Google Scholar