Article contents
No elementary embedding from v into v is definable from parameters
Published online by Cambridge University Press: 12 March 2014
Extract
In 1970, Kenneth Kunen showed that there is no non-trivial elementary embedding of the universe V into itself [2] using the axiom of choice. Kunen remarked in his paper that the result can be formalized in Morse-Kelley theory of sets and classes. In this paper, we will work within ZF, Zermelo-Fraenkel axioms, and deal with embeddings definable with a formula and a parameter.
In ZF, a “class” is usually synonymous with “property”, that is a class definable with a parameter, C = {x: φ(x,p)}, where φ is a formula in the language [∈}. Using this convention, let j be a class. Then “j is an elementary embedding of V into V” is not a single statement but a schema of statements “j preserves ψ” for each formula ψ. We prove that this schema is expressible in the language {∈} by a single formula:
Lemma. An embedding j: V → V is elementary iff j preservesψ.
Here ψ(α, ψ, a) is the property “a is an ordinal, φ is a formula and Vα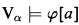 .”
.”
The lemma is of course a schema of lemmas, one for each formula denning j and for each ψ to be preserved.
Using this we prove our theorem in ZF (again, a schema of theorems.):
Theorem 1.1. There is no nontrivial definable elementary embedding j: V → V.
Many symbols and their definitions follow those used by Drake's book [1]. The formula Sat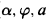 expresses the satisfaction relation
expresses the satisfaction relation 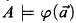 . The formula Fmla(u) expresses that u is the Gödel-set for a formula.
. The formula Fmla(u) expresses that u is the Gödel-set for a formula.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1999
References
REFERENCES
- 9
- Cited by

