Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T17:33:05.744Z Has data issue: false hasContentIssue false
  • English
  • Français

The noncommutativity of random and generic extensions

Published online by Cambridge University Press:  12 March 2014

J.K. Truss
J.K. Truss*
Affiliation:
Paisley College of Technology, Paisley, Renfrewshire, Scotland
Get access Rights & Permissions [Opens in a new window]

Extract

Throughout, M will denote a transitive model of ZFC. Using the terms “random” and “generic” in the sense of [1], one may ask whether there can exist real numbers x and y such that x is generic over M[y] and y is random over M[x]. We shall see below by an elementary argument that this is not possible, and so, in a crude sense at least, random and generic extensions do not commute. This does not however rule out the possibility of a weaker commutativity. Let B be the complete Boolean algebra (in M) for adjoining a random real followed by a generic real and C be the complete Boolean algebra for adjoining a generic real followed by a random real. Then it still might be the case that B and C are isomorphic. This also fails, though, and we shall prove this by establishing the following combinatorial properties of MB and MC:

but

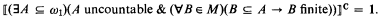
In addition this will show that C cannot be embedded as a complete subalgebra of B.

The property satisfied by B is reminiscent of calibre ℵ1 [2]. B would have calibre if we could replace “infinite” by “uncountable”, and this occurs if Martin's Axiom 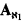holds in M. To obtain the nonisomorphism of B and C in general necessitated looking at the weaker property.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 4 , December 1983 , pp. 1008 - 1012
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Solovay, R.M., A model of set-theory in which every set of reals is Lebesgue measurable, Annals of Mathematics (2), vol. 92 (1970), pp. 1–56CrossRefGoogle Scholar
[2]Truss, J.K., Sets having calibre ℵ1, Logic Colloquium 76 (Gandy, R.O. and Hyland, J.M.E., editors), North-Holland, Amsterdam, 1977, pp. 595–612.Google Scholar