Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
2011.
Backs, Karl
Jackson, Steve
and
Mauldin, R. Daniel
2015.
CH, V=L, disintegration of measures, and Π11 sets.
Advances in Mathematics,
Vol. 274,
Issue. ,
p.
76.

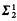 , graphs. If
, graphs. If 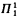 . Assuming stronger set theoretic axioms, we identify the least pointclass such that any such coanalytic
. Assuming stronger set theoretic axioms, we identify the least pointclass such that any such coanalytic 