Note on an induction axiom

Extract

Let θ(ν) be a formula in the first-order language of arithmetic and let

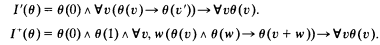
In this note we study the relationship between the schemas I′ and I⁺.

Our interest in I⁺ lies in the fact that it is ostensibly a more reasonable schema than I′. For, if we believe the hypothesis of I⁺(θ) then to verify θ(n) only requires at most 2log₂(n) steps, whereas assuming the hypothesis of I′(θ) we require n steps to verify θ(n). In the physical world naturally occurring numbers n rarely exceed 10¹⁰⁰. For such n applying 2log₂(n) steps is quite feasible whereas applying n steps may well not be.

Of course this is very much an anthropomorphic argument so we would expect that it would be most likely to be valid when we restrict our attention to relatively simple formulas θ. We shall show that when restricted to open formulas I⁺ does not imply I′ but that this fails for the classes Σ_n, Π_n, n ≥ 0.

We shall work in PA⁻, where PA⁻ consists of Peano's Axioms less induction together with

∀u, w(u + w = w + u ∧ u · w = w · u),

∀u, w, t ((u + w) + t = u + (w + t) ∧ (u · w) · t = u · (w · t)),

∀u, w, t(u · (w + t) = u · w + u · t),

∀u, w(u ≤ w ↔ ∃t(u + t = w)),

∀u, w(u ≤ w ∨ w ≤ u),

∀u, w, t(u + w = u + t → w = t).

The reasons for working with PA⁻ rather than Peano's Axioms less induction is that our additional axioms, whilst intuitively reasonable, will not necessarily follow from some of the weaker forms of I⁺ which we shall be considering. Of course PA⁻ still contains those Peano Axioms which define + and

Notice that, trivially, PA⁻ ⊦ I′(θ) → I⁺(θ) for any formula θ.