Article contents
A note on the undefinability of cuts
Published online by Cambridge University Press: 12 March 2014
Extract
The results in this paper were motivated by the following result due to R. Solovay.
Theorem 1 (Solovay). Let M be a nonstandard model of Peano's first order axioms P and let I ⊂e M (i.e. ϕ ≠ ⊂ M and I is closed under < and successor). Then for each of the functions 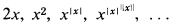 we can define J ⊆e I in ‹M, I› such that J is closed under that function. (∣x∣ denotes [log2(x)].)
we can define J ⊆e I in ‹M, I› such that J is closed under that function. (∣x∣ denotes [log2(x)].)
Proof. Just notice that the cuts defined by
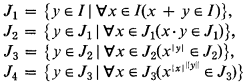
are successively closed under 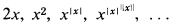
In view of Theorem 1, the following question was raised by R. Solovay: Can we define J ⊆ I in ‹M, I› such that J is closed under exponentiation? In Theorem 2 we show that the answer is “no”. Theorem 3 is based on Theorem 2 and extends the technique to cuts which are models of subsystems of P.
To prove both theorems we shall need an estimate due to R. Parikh (see [1], especially the proof of Theorem 2.2a). For the sake of completeness, and also to introduce some notation we shall sketch Parikh's estimate in the next section. At all times we shall give the easiest estimates which still work rather than the sharpest ones.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
References
REFERENCES
- 19
- Cited by

