Article contents
A note on valuation definable expansions of fields
Published online by Cambridge University Press: 12 March 2014
Extract
In this note, we consider models of the theories of valued algebraically closed fields and convexly valued real closed fields, their reducts to the pure field or ordered field language respectively, and expansions of these by predicates which are definable in the valued field. We show that, in terms of definability, there is no structure properly between the pure (ordered) field and the valued field. Our results are analogous to several other definability results for reducts of algebraically closed and real closed fields; see [9], [10], [11] and [12]. Throughout this paper, definable will mean definable with parameters.
Theorem A. Let ℱ = (F, +, ×, V) be a valued, algebraically closed field, where V denotes the valuation ring. Let A be a subset ofF n definable in ℱv . Then either A is definable in ℱ = (F, +, ×) or V is definable in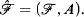 .
.
Theorem B. Let ℛv = (R, <, +, ×, V) be a convexly valued real closed field, where V denotes the valuation ring. Let Abe a subset ofR n definable in ℛv . Then either A is definable in ℛ = (R, <, +, ×) or V is definable in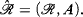 .
.
The proofs of Theorems A and B are quite similar. Both ℱv and ℛv admit quantifier elimination if we adjoin a definable binary predicate Div (interpreted by Div(x, y) if and only if v(x) ≤ v(y)). This is proved in [14] (extending [13]) in the algebraically closed case, and in [4] in the real closed case. We show by direct combinatorial arguments that if the valuation is not definable then the expanded structure is strongly minimal or o-minimal respectively. Then we call on known results about strongly minimal and o-minimal fields to show that the expansion is not proper.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
- 1
- Cited by

