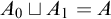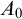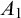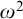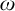NOTES ON SACKS’ SPLITTING THEOREM

Abstract

We explore the complexity of Sacks’ Splitting Theorem in terms of the mind change functions associated with the members of the splits. We prove that, for any c.e. set A, there are low computably enumerable sets $A_0\sqcup A_1=A$ splitting A with $A_0$ and $A_1$ both totally $\omega ^2$-c.a. in terms of the Downey–Greenberg hierarchy, and this result cannot be improved to totally $\omega $-c.a. as shown in [9]. We also show that if cone avoidance is added then there is no level below $\varepsilon _0$ which can be used to characterize the complexity of $A_1$ and $A_2$.

1 Introduction

Beginning with Friedberg’s paper [11], some of the earliest theorems in computability theory are those concerning splittings of computably enumerable (c.e.) sets. We say that $A_0\sqcup A_1=A$ is a splitting of A if $A_0, A_1$ are c.e., disjoint, and $A_0\cup A_1=A$ . One of the reasons that splitting theorems have interest is their interactions with the c.e. degrees. If $A_0\sqcup A_1=A$ , then deg $(A_0)\lor $ deg $(A_1)=$ deg $(A)$ holds in the Turing (and in fact weak truth table) degrees.

One form of Sacks’ famous splitting theorem [13] asserts the following.

Theorem 1.1 (Sacks [13])

For each noncomputable c.e. set A there is a splitting $A_0\sqcup A_1=A$ with $A_0$ and $A_1$ both c.e. and of low degree with $A_0|_T A_1$ .

In particular, there is no least c.e. degree, all c.e. degrees are join reducible, and the low c.e. degrees generate the computably enumerable ones. For more on the many interactions of splittings of c.e. sets with the c.e. degrees and other topics in classical computability theory, we refer to the somewhat dated but extensive paper [10].

Ever since Soare’s classic paper [15], Sacks Splitting Theorem is pointed as a quintessential example of a finite injury argument of “unbounded type.” By this we mean the following. The standard simple proof of the existence of a c.e. set of low degree, or of the Friedberg–Muchnik Theorem, as per Soare’s book [16] (or any other standard text), uses a finite injury priority argument where requirements are injured at most a computable number of times. Recall that the Friedberg–Muchnik Theorem says that there are c.e. sets A and B with incomparable Turing degrees. This differs from Sacks’ splitting theorem (Theorem 1.1) in that Sacks’ splitting theorem requires additionally A and B to be a partition of a given non-computable c.e. set.

In the standard proof of the Friedberg–Muchnik Theorem each non-computability requirement $R_{2e}$ is injured at most $2^e$ many times. This makes the relevant sets not just low, but superlow. That is, for each $i\in \{0,1\}$ , not only is $A_i^{\prime }\equiv _T \emptyset '$ but $A_i^{\prime }\equiv _{tt}\emptyset '$ , since each partial function $f\le _T A_i$ can be computed with an approximation with at most a computable number of mind-changes in the sense of the limit lemma.

When teaching computability theory, we always point out that Sacks’ Splitting Theorem has a completely different character since, whilst both $A_0 $ and $A_1$ splitting A are low, we have no a priori knowledge of how many injuries the requirements will have.

In the present paper we address the following question:

Question 1.2. Is there some way to quantify the difference between the Friedberg–Muchnik Theorem and Sacks’ Splitting Theorem?

1.1 How should we answer this question?

Could there be some proof of Sacks’ Splitting Theorem avoiding the feature of “unbounded but finite injury,” so that it is simply an artifact of the standard proof rather than a necessary feature?

One possible way to answer this would be using “Reverse Recursion Theory” by asking what amount of induction is needed for proving Sacks’ Splitting Theorem in fragments of arithmetic. In this setting we do know that there is a difference. Mytilinaios [12] showed how to use an analog of Shore’s Blocking [14] to prove this theorem in $P^-+I\Sigma _1$ , whereas Chong and Mourad [3] showed that the Friedberg–Muchnik Theorem can be proven in the weaker system of $P^-+B\Sigma _1$ , and also proved that Theorem 1.1 fails in some model of $P^-+B\Sigma _1$ . We include these results to mention one possible approach towards answering the question of what level of “unbounded injury” is necessary for Sacks’ Splitting Theorem. Here the interpretation is that the system with $B\Sigma _1$ corresponds to computably bounded injury. We refer the reader to Chong, Li, and Yang [2] for more on this topic.

1.2 Using classical notions

If we wish to use classical computability theory, we need to find some way to show that the arguments must be different.

Perhaps lowness might be the key. As mentioned above, we know that if a set is constructed to be low using a standard argument it will often also be superlow where X is superlow if $X'\equiv _{tt} \emptyset '$ . How does this work for splitting theorems?

Downey and Ng [9] have shown that if we consider splitting with low replaced by superlow then then Sacks’ Splitting result fails. Indeed, as we see in Theorem 1.3, a stronger result is true.

The setting of the present paper. In this paper, we will take a different tack to attempt to understand the complexity of the argument needed for Sacks’ Splitting Theorem. We will use the new Downey–Greenberg hierarchy [4, 5] of computably enumerable degrees. This hierarchy seeks to classify the complexity of c.e. degrees according to the ease of approximation of total functions computable from them. The Downey–Greenberg Hierarchy was inspired by the array computable c.e. degrees defined by Downey, Jockusch, and Stob [8], where a c.e. degree $\mathbf {a}$ is array computable iff there is a computable order g (i.e., a computable nondecreasing unbounded function) such that if function $f\le _T \mathbf {a}$ , then f has a $\Delta _2^0$ approximation $f(\cdot )=\lim _s f(\cdot ,s)$ such that for all x,

$$ \begin{align*}|\{s\mid f(x,s+1)\ne f(x,s)\}|\le g(x).\end{align*} $$

It is easy to show that all superlow c.e. sets are array computable. But there are non-low c.e. sets that are array computable [8]. Thus the notion of array computability is a measure of describing the fact that the degree is easy to approximate in a very specific way. We now know that array computable degrees capture the combinatorics of a wide class of constructions in computability theory. For instance, $\mathbf {a}$ is array non-computable (i.e., not array computable) iff it can compute

• • c.e. set of infinitely often maximal plain Kolmogorov complexity,

• • disjoint pairs of c.e. sets $A,B$ , with $\omega -(A\sqcup B)$ infinite and no set separating A from B of degree $\mathbf {0'}$ ,

• • a perfect thin $\Pi _1^0$ class, etc.

There are many other characterizations of array computability and we refer the reader to [5], for example.

Following a suggestion of Joe Miller, in [6], array computability was generalized to what is called totally $\omega $ -c.a. where $\textbf {a}$ has this property iff for all $f\le _T \textbf {a}$ , there is a computable order g such that f has a $\Delta _2^0$ approximation $f(\cdot )=\lim _s f(\cdot ,s)$ such that for all x,

$$ \begin{align*}|\{s\mid f(x,s+1)\ne f(x,s)\}|\le g(x).\end{align*} $$

That is, $\mathbf {a}$ is “nonuniformly” array computable, but is still effectively approximable. In [6], Downey, Greenberg, and Weber showed that the totally $\omega $ -c.a. degrees indeed capture a wide class of combinatorial constructions in computability theory, and are naturally definable in the c.e. degrees.

To capture further combinatorics and definability, Downey and Greenberg [4, 5] extended the notion of being totally $\omega $ -c.a. as follows. For computable ordinals below $\varepsilon _0$ , we can associate a canonical effective Cantor Normal Form. That is, if, for example, $\alpha <\omega ^3$ , say, then $\alpha $ is specified by a triple $(n_0,n_1,n_2)$ representing that $\alpha =n_0\omega ^2+n_1\omega +n_2.$ If $f(x)$ is $\alpha $ -c.a. then it would have a $\Delta _2^0$ approximation $f(x,s)$ where initially $f(x,s+1)\ne f(x,s)$ can change $n_2$ many times, and after that it would move to $n_0\omega ^2+(n_1-1)\omega + n_2^{\prime }$ and have another $n_2^{\prime }$ many further changes to move to $n_0\omega ^2+ (n_1-2)n_1+n_2^{\prime \prime },$ etc., with each change on one of the ordinals allowing a free choice for those right of it. Several natural classical constructions seems to correlate to levels of the resulting (proper) hierarchy. For instance, $\omega ^{\omega }$ captures embeddings of the 1–3–1 lattice into the c.e. degrees and being totally $\omega $ -c.a. captures certain other configurations, as well as constructions from Kolmogorov complexity (see [4, 5]).

1.3 Our results using this hierarchy

Downey and Ng [9] did not just prove that not every c.e. set can be split into a pair of superlow ones. Downey and Ng showed the following:

Theorem 1.3 (Downey and Ng [9])

There is a c.e. degree $\mathbf {a}$ such that if $\mathbf {a_0}\cup \mathbf {a_1}=\mathbf {a}$ in the c.e. degrees, then one of $\mathbf {a_0}$ or $\mathbf {a_1}$ is not totally $\omega $ -c.a.

In passing, we mention that, in the same paper, Downey and Ng also showed that every high c.e. degree is the join of two totally $\omega $ -c.a. c.e. degrees. This second result extends a classical theorem of Bickford and Mills [1] who showed that $\mathbf {0'}$ is the join of two superlow c.e. degrees. However, in [9] it is also shown that there are (super-)high c.e. degrees that are not the joins of two superlow degrees.

Thus, if we use the Downey–Greenberg hierarchy for the classification of the complexity of c.e. sets resulting from an incomparable splitting, we cannot hope to do better than $\omega ^2$ .

In Section 2, we show that the classical Sacks’ construction proves that a c.e. set A can be split into a pair of totally $\omega ^{\omega }$ -c.a. (low) c.e. sets (see Theorem 2.1).

However, in Section 3 we find a novel way of proving Sacks’ Splitting in a certain dynamic way (with perhaps other applications), which allows us to show the following.

Theorem 1.4. Every c.e. set can be split into a pair of low c.e. sets which are totally $\omega ^2$ -c.a.

1.4 Where the injury becomes unbounded

The original Sacks’ Splitting Theorem has a stronger form.

Theorem 1.5 (Sacks [13])

For each noncomputable c.e. set A and noncomputable $\Delta _2^0$ set C there is a splitting $A_0\sqcup A_1=A$ with $A_0$ and $A_1$ both of low degree and $C\not \le _T A_i$ for $i\in \{0,1\}$ .

In the final section, we will show that Theorem 1.5 does need a finite injury argument of “unbounded type.” We prove the following theorem.

Theorem 1.6. Let $\alpha <\varepsilon _0$ . Then there exist noncomputable c.e. sets A and C such that for all c.e. splittings $A_0\sqcup A_1=A$ of A, if $A_0$ is totally $\alpha $ -c.a. then $C\le _T A_1$ .

Hence no level of the Downey–Greenberg Hierarchy suffices to capture this version of Sacks’ Splitting Theorem.

Indeed, we prove that Theorem 1.6 holds for degrees.

Theorem 1.7. Let $\alpha <\varepsilon _0$ . Then there exist c.e. degrees $\mathbf {a}$ and $\mathbf c> \mathbf {0}$ such that for all c.e degrees $\mathbf {a}_0,\mathbf {a}_1$ with $\mathbf {a}_0\lor \mathbf {a}_1=\mathbf {a}$ , if $\mathbf {a}_0$ is totally $\alpha $ -c.a. then $\mathbf c\le \mathbf {a}_1$ .

This proof is a slight modification of the proof of Theorem 1.6.

We remark that this is the first example of a classical result which has been shown to need finite injury of unbounded type, at least as measured by the Downey–Greenberg Hierarchy.

1.5 Conventions

We refer to [16] or the computability section of [7] as a general reference to our notation and terminology. We tend to use the Lachlan convention that appending $[s]$ to a parameter, indicates its state at stage s. Uses will be lower case letters of the functionals. Parameters don’t change from stage to stage unless indicated otherwise. Uses are monotone in argument and stage number.

2 Splitting a c.e. set into $\omega ^{\omega }$ -c.a. c.e. sets

Before we prove our main result we show that, by a straightforward variant of Sacks’ splitting technique, we can split any c.e. set into totally $\omega ^{\omega }$ -c.a. c.e. sets.

Theorem 2.1. For any c.e. set A there is a c.e. splitting $A = A_0 \sqcup A_1$ such that $A_0$ and $A_1$ are totally $\omega ^{\omega }$ -c.a. and low.

Proof Given a c.e. set A, we have to split A into disjoint low c.e. sets $A_0$ and $A_1$ meeting the global requirements

$$ \begin{align*} \mathcal{R}^{global}_{i,e}: \; \text{ If } \Phi^{A_i}_e \text{ is total then } \Phi^{A_i}_e \text{ is } \omega^{\omega}\text{-c.a.} \end{align*} $$

for $e \geq 0$ and $i \leq 1$ . We split $\mathcal {R}^{global}_{i,e}$ into local requirements $\mathcal {R}_{2\langle e,x\rangle +i}$ ( $ x \geq 0$ ) where requirement $\mathcal {R}_{2\langle e,x\rangle +i}$ attempts to preserve the computation $\Phi ^{A_{i,s}}_{e,s}(x)$ (whenever this computation is defined) by restraining numbers $< \varphi ^{A_{i,s}}_{e}(x)$ from $A_i$ . I.e., if $\Phi ^{A_{i,s}}_{e,s}(x) \downarrow $ and a number $< \varphi ^{A_{i,s}}_{e}(x)$ enters A at stage $s+1$ then $\mathcal {R}_{2\langle e,x\rangle +i}$ requires that this number is put into $A_{1-i}$ . We will argue that if we give a requirement higher priority if its index is lesser, then this strategy suffices to meet the global requirements hence to make $A_0$ and $A_1$ totally $\omega ^{\omega }$ -c.a. In order to show this, we first describe the construction more formally.

W.l.o.g. assume that A is infinite, fix a 1–1 computable function a enumerating A, and let $A_{s} = \{a(t): t < s\}$ . Note that here, $A_s$ refers to the set of elements enumerated into A by stage s and is not to be confused with the sets $A_0$ and $A_1$ . The sets $A_0$ and $A_1$ are enumerated in stages where at stage $s+1$ we decide whether $a(s)$ is put into $A_0$ or $A_1$ . So $A_{i,s}= \{a(t): t < s \; \& \; a(t)\in A_i\}$ . The restraint imposed by requirement $\mathcal {R}_{2\langle e,x\rangle +i}$ on $A_i$ at stage $s+1$ is defined by

$$ \begin{align*}r(2\langle e,x\rangle +i,s)=\begin{cases} \varphi^{A_{i,s}}_{e}(x), & \text{if } \Phi^{A_{i,s}}_{e,s}(x) \downarrow, \\ 0, & \text{otherwise}. \end{cases} \end{align*} $$

Then, at stage $s+1$ , $a(s)$ is put into $A_1$ if the least n such that $a(s) < r(n,s)$ is even (or if no such n exists), and $a(s)$ is put into $A_0$ otherwise. Moreover, we call $\mathcal {R}_{2\langle e,x\rangle +i}$ an i-requirement and an i-e-requirement, and we say that requirement $\mathcal {R}_{2\langle e,x\rangle +i}$ is injured at stage $s+1$ if $a(s) < r(2\langle e,x\rangle +i,s)$ and $a(s)$ is enumerated into $A_i$ . (Note that i-requirements impose restraint on $A_i$ .)

This completes the construction.

Obviously, the sets $A_0$ and $A_1$ are disjoint and c.e. and $A = A_0 \cup A_1$ . So $A = A_0\sqcup A_1$ . Moreover, just as in the standard proof of Sacks’ Splitting Theorem, it follows by a straightforward induction on $n \geq 0$ that any requirement $\mathcal {R}_{n}$ is injured at most finitely often. So we may fix $s_n$ minimal such that $\mathcal {R}_{n}$ is not injured after stage $s_n$ . Then, for $n = 2\langle e,x\rangle +i$ , any computation $\Phi ^{A_i,t}_{e,t}(x)$ existing at a stage $t \geq s_n$ is preserved, hence

(1) $$ \begin{align} \Phi^{A_i}_e(x) \uparrow \; \Leftrightarrow \; \forall \; t \geq s_{2\langle e,x\rangle+i} \; (\Phi^{A_i,t}_{e,t}(x) \uparrow). \end{align} $$

So, in particular, the requirements $\mathcal {R}_{2\langle e,e\rangle +i}$ ensure that the standard lowness requirements

$$ \begin{align*}\mathcal{Q}_{2e+i}: \; \exists^{\infty} s (\Phi^{A_i,s}_{e,s}(e) \downarrow) \; \Rightarrow \Phi^{A_i}_e(e) \downarrow\end{align*} $$

are satisfied ( $e \geq 0, i \leq 1$ ). Hence the sets $A_0$ and $A_1$ are low.

It remains to show that the global $\omega ^{\omega }$ -c.a. requirements $\mathcal {R}^{global}_{i,e}$ are met. Fix $i \leq 1$ and $e \geq 0$ such that $\Phi ^{A_i}_e$ is total. Define the canonical computable approximation $\psi $ of $\Phi ^{A_i}_e$ induced by $\{ \Phi ^{A_{i,s}}_{e,s}\}_{s \geq 0}$ by letting

$$ \begin{align*} \psi(x,s) = \Phi^{A_{i,s'}}_{e,s'}(x) \; \text{ for the least } s' \geq s \text{ such that } \Phi^{A_{i,s'}}_{e,s'}(x) \downarrow. \end{align*} $$

Then it suffices to define a computable function $c: \omega \times \omega \to \omega ^{\omega }$ such that, for $x, s \geq 0$ ,

(2) $$ \begin{align} c(x,s+1) \leq c(x,s) \end{align} $$

and

(3) $$ \begin{align} \psi(x,s+1) \not= \psi(x,s) \; \Rightarrow \; c(x,s+1) \not= c(x,s). \end{align} $$

The definition of c is based on the following observations where we let $n_x = 2\langle e, x \rangle +i$ .

Claim 1. (a) If $\psi (x,s+1) \not = \psi (x,s)$ then $\mathcal {R}_{n_x}$ is injured at stage $s+1$ .

(b) If a requirement $\mathcal {R}_n$ is injured at stage $s+1$ then there is a number $n' < n$ such that $r(n',s+1)=r(n',s)$ and $a(s) < r(n',s)$ , hence

(4) $$ \begin{align} |\overline{A_{s+1}} \upharpoonright r(n',s+1)| < |\overline{A_{s}} \upharpoonright r(n',s)|. \end{align} $$

(c) If $r(n,s+1) \not = r(n,s)$ then $r(n,s)=0$ or $\mathcal {R}_n$ is injured at stage $s+1$ .

Proof (a) Assume $\psi (x,s+1) \not = \psi (x,s)$ . Then, by definition of $\psi $ , $\psi (x,s) = \Phi ^{A_{i,s}}_{e,s}(x) \downarrow $ and either $\Phi ^{A_{i,s+1}}_{e,s+1}(x) \uparrow $ or $\psi (x,s+1) = \Phi ^{A_{i,s+1}}_{e,s+1}(x) \downarrow $ . So, in either case, $\Phi ^{A_{i,s}}_{e,s}(x) \downarrow \not = \Phi ^{A_{i,s+1}}_{e,s+1}(x)$ . This implies that $r(n_x,s) = \varphi ^{A_{i,s}}_{e}(x)$ and $A_{i,s+1} \upharpoonright \varphi ^{A_{i,s}}_{e}(x) \not = A_{i,s} \upharpoonright \varphi ^{A_{i,s}}_{e}(x)$ . So $\mathcal {R}_{n_x}$ is injured at stage $s+1$ .

(b) Assume that $\mathcal {R}_{n}$ is injured at stage $s+1$ . Fix $i'$ such that $\mathcal {R}_{n}$ is an $i'$ -requirement. Then, by construction, $a(s)$ is put into $A_{i'}$ and there is a $(1-i')$ -requirement $\mathcal {R}_{n'}$ such that $n' < n$ and $a(s) < r(n',s)$ . Finally, by $A_{1-i',s+1} = A_{1-i',s}$ and $r(n',s)> 0$ , it holds that $r(n',s) = \varphi ^{A_{1-i',s}}_{e'}(x') = \varphi ^{A_{1-i',s+1}}_{e'}(x') = r(n',s+1)$ for the unique numbers $e',x' \geq 0$ such that $n'=2 \langle e',x' \rangle +(1-i')$ .

(c) Assume that $r(n,s+1) \not = r(n,s)$ and $r(n,s)> 0$ , and fix $e',x' \geq 0$ and $i' \leq 1$ such that $n=2 \langle e',x' \rangle +i'$ . Then, by $r(n,s)> 0$ , $\Phi ^{A_{i',s}}_{e',s}(x') \downarrow $ and $r(n,s) = \varphi ^{A_{i',s}}_{e'}(x')$ . By $r(n,s+1) \not = r(n,s)$ , this implies that either $\Phi ^{A_{i',s+1}}_{e',s+1}(x')$ is undefined or $\Phi ^{A_{i',s+1}}_{e',s+1}(x')$ is defined but $\varphi ^{A_{i',s+1}}_{e',s+1}(x') \downarrow \not = \varphi ^{A_{i',s}}_{e',s}(x')$ . It follows that $a(s) < \varphi ^{A_{i',s}}_{e'}(x') = r(n,s)$ and $a(s)$ is put into $A_{i'}$ at stage $s+1$ . So $\mathcal {R}_{n}$ is injured at stage $s+1$ .

This completes the proof of Claim 1.

Now, for the definition of the computable function c, we represent the ordinals $< \omega ^{\omega }$ by nonempty finite tuples of nonnegative integers where the $(k+1)$ -tuple $(a_k, \dots , a_0)$ represents the ordinal

$$ \begin{align*}\sum_{i=0}^k a_i \omega^i = a_k \omega^k + \dots + a_2 \omega^2 + a_1 \omega + a_0.\end{align*} $$

Then $c(x,s)$ is defined by

$$ \begin{align*}\begin{array}{lll} c(x,s) & = & (c_0(0,s), c_1(0,s), c_0(1,s), c_1(1,s), \dots, c_0(n_x-1,s), c_1(n_x-1,s)) \\ & = & \sum_{n < n_x} \bigg(c_0(n,s) \cdot \omega^{2(n_x-n)-1} +c_1(n,s) \cdot \omega^{2(n_x-n)-2}\bigg), \end{array} \end{align*} $$

where

$$ \begin{align*}c_0(n,s)=\begin{cases} 0, & \text{if } r(n,s)>0, \\ 1, & \text{otherwise}, \end{cases} \text{ } \; \; \text{ and } \; \; \text{ } c_1(n,s) = |\overline{A_s} \upharpoonright r(n,s)|. \end{align*} $$

(Here and in the following we assume that $n_x> 0$ . If $n_x=0$ then, by Claim 1(a), $\psi (x,s+1) = \psi (x,s)$ for all stages $s \geq 0$ . So (2) and (3) will hold if we let $c(x,s) =0$ for all $s \geq 0$ .)

Obviously, $c(x,s)$ is computable. So it only remains to establish (2) and (3).

For a proof of (2) fix x and s such that $c(x,s+1) \not = c(x,s)$ . Choose $2n+i'$ minimal such that $i' \leq 1$ , $n < n_x$ , and $c_{i'}(n,s+1) \not = c_{i'}(n,s)$ . It suffices to show that $c_{i'}(n,s+1) < c_{i'}(n,s)$ . Note that requirement $\mathcal {R}_n$ is not injured at stage $s+1$ (namely, otherwise, it would follow by Claim 1(b) that there is a number $n' < n$ such that $c_1(n',s+1) < c_1(n',s)$ contradicting minimality of $2n+i'$ ). Now distinguish the following two cases. First assume that $r(n,s+1)=r(n,s)$ . Then $c_0(n,s+1)=c_0(n,s)$ , hence $i'=1$ . By assumption this implies that

$$ \begin{align*}|\overline{A_{s+1}} \upharpoonright r(n,s)| = c_{i'}(n,s+1) \not= c_{i'}(n,s) = |\overline{A_{s}} \upharpoonright r(n,s)|.\end{align*} $$

As $\overline {A_{s+1}} \subseteq \overline {A_s}$ it follows that $c_{i'}(n,s+1) < c_{i'}(n,s)$ . Finally, assume that $r(n,s+1)\not =r(n,s)$ . Since $\mathcal {R}_n$ is not injured at stage $s+1$ , it follows by Claim 1(c) that $r(n,s)=0$ . So, by case assumption, $r(n,s+1)> 0$ , and we may conclude that $i'=0$ and $c_{0}(n,s+1)=0 < 1 = c_{0}(n,s)$ . This completes the proof of (2).

Finally, for a proof of (3), fix x and s such that $\psi (x,s+1) \not = \psi (x,s)$ . Then, by Claim 1(a) and (b), there is a number $n' < n_x$ such that (4) holds whence $c_1(n',s+1) < c_1(n',s)$ . By definition of c, this implies $c(x,s+1) \not = c(x,s)$ . So (3) holds.

This completes the proof of Theorem 2.1.

3 The $\omega ^2$ -proof

Theorem 3.1. Given a c.e. set A there are c.e. sets $A_0$ and $A_1$ such that $A= A_0\sqcup A_1$ and $A_0$ and $A_1$ have totally $\omega ^2$ -c.a. degree.

Proof We note that the proof does not make $A_0$ and $A_1$ Turing incomparable. If A is totally $\omega ^2$ -c.a. then we can use the usual Sacks’ splitting theorem to obtain Turing incomparable $A_0$ and $A_1$ . The proof is an infinite injury, although we will not be using a tree to organize the construction. Rather, we will be using a mechanism similar to e-states used in the maximal set construction.

3.1 Notation

We fix a 1–1 enumeration of A, and let $a_s$ be the element enumerated into A at stage s. We write $(e,x,i)$ to stand for the subrequirement that wants to restrain the use of $\Phi _e(A_i;x)$ . We also write $\varphi _e(x,i)[s]$ to be the use of the computation $\Phi _e(A_i;x)$ at stage s. Two triples $(e,x,i)$ and $(e',x',i')$ are said to be of the same type if $i=i'$ .

Instead of ordering the triples $(e,x,i)$ by priority, we will instead bunch up several triples of the same type and view them to be of the same priority. In order to facilitate this, we will introduce the notion of blocks. A block $\mathcal {B}^i_k$ is a collection of triples of type i who are assigned the same priority. However, we will differentiate the priority between different blocks. The priority ordering between different blocks are: $\mathcal {B}^0_0<\mathcal {B}^1_0<\mathcal {B}^0_1<\mathcal {B}^1_1<\mathcal {B}_2^0<\mathcal {B}_2^1<\cdots .$ This priority ordering is fixed, but the contents of each block will change. $\mathcal {B}^i_n$ will only contain triples of the form $(e,x,i)$ where $e\leq n$ . At each stage s, we denote $r^i_n[s]$ to be the maximum value of $\varphi _e(x,i)$ where $(e,x,i)\in \mathcal {B}^i_n$ , and $R^i_n$ to be the maximum value of $r^{i'}_{n'}$ where $\mathcal {B}^{i'}_{n'}\leq \mathcal {B}^i_n$ . If P is a parameter then $P[s]$ denotes the value of P at the beginning of stage s.

We denote $\mathtt {Conv}(\mathcal {B}^i_n)$ for a block $\mathcal {B}^i_n$ to be a finite string of length $n+1$ over the alphabet set $\{\infty ,f\}$ , defined such that $\mathtt {Conv}\left (\mathcal {B}^i_n\right )(e)=\infty $ if and only if $\mathcal {B}^i_n$ contains a triple of the form $(e,x,i)$ , for each $e\leq n$ . We order these strings lexicographically, where $\mathtt {Conv}(\mathcal {B})< \mathtt {Conv}(\mathcal {B}')$ if $\mathtt {Conv}(\mathcal {B})$ is lexicographically to the left of $\mathtt {Conv}(\mathcal {B}')$ (with the usual convention of $\infty $ being to the left of f; the value $\infty $ standing for “total” and value f for “partial”). To initialize a block $\mathcal {B}^i_n$ means to make it empty.

We shall need to keep track of the totality of $\Phi _e(A_i;x)$ ; the standard way of doing this is to define the parameter $l(e,i)[s]=$ largest $x<s$ such that $\Phi _e(A_i;y)[s]\downarrow $ for every $y<x$ . At every stage s, and $i=0,1$ , we let $\delta _i[s]$ be a string of length s over $\{\infty ,f\}$ defined by induction on $e< s$ : Suppose $\delta _i[s]\upharpoonright e$ has been defined. We set $\delta _i[s](e)=\infty $ if and only if $l(e,i)[s]>t$ , where $t<s$ is the largest stage such that $\delta _i[t]\supseteq \left (\delta _i[s]\upharpoonright e\right )\widehat {\phantom {\eta }}\infty $ or $\delta _i[t]<\delta _i[s]\upharpoonright e$ . (We take $t=0$ if this does not exist.)

3.2 Discussion of the proof

We have seen in Section 2 that the standard proof of Sacks’ Splitting Theorem will produce a set splitting $A_0\sqcup A_1$ of A where $A_0$ and $A_1$ are of totally $\omega ^{\omega }$ -c.a. degree. In order to improve this to $\omega ^2$ -c.a., we shall have to organize the priority of the requirements dynamically. The basic unit in the construction is that of a triple $(e,x,i)$ , which represents the (sub)-requirement that wants to restrain the use of a convergent $\Phi _e(A_i;x)$ . Obviously two triples $(e,x,i)$ and $(e',x',i')$ are in direct conflict only if $i\neq i'$ . In order to fully exploit this fact, we will place different triples of the same type in a block. Since triples of the same type are not in direct conflict with each other, we will consider all triples in the same block to be of the same relative priority, and we will only set priority between different blocks. The priority ordering between blocks is fixed, but the elements of each block will change as the construction proceeds.

Let’s first consider a single pair of requirements, $\Phi _0(A_0)$ and $\Phi _0(A_1)$ , and assume both to be total. Each block $\mathcal {B}^i_n$ contains finitely many triples of the form $(0,x,i)$ , with $A_i$ -restraint $R^i_n$ . To illustrate, let’s fix $i=0$ and some x, and count the number of changes to $\Phi _0(A_0;x)$ . Suppose that $(0,x,0)\in \mathcal {B}^i_n[s_1]$ for some n, where $s_1$ is the first stage we begin monitoring $\Phi _0(A_0;x)$ . If a number $a_s$ enters A, we must enumerate $a_s$ immediately into either $A_0$ and $A_1$ . This decision is made based on the highest priority block $\mathcal {B}^{i'}_{n'}$ that would be injured by $a_s$ entering $A_{i'}$ , and we would put $a_s$ into $A_{1-i'}$ instead. Doing so will obviously injure all $1-i'$ -blocks of priority lower than that of $\mathcal {B}^{i'}_{n'}$ , so we must initialize them.

Thus in order for the computation $\Phi _0(A_0;x)$ to be injured, we must see some number $a_s<R^1_{n-1}[s_1]$ enter A. Assuming that $\mathcal {B}^1_0,\ldots ,\mathcal {B}^1_{n-1}$ are not injured, the restraint $R^1_{n-1}$ is not increased after $s_1$ , and thus the number of times $\Phi _0(A_0;x)$ can be injured is at most $R^1_{n-1}[s_1]$ . An ordinal bound of $\omega $ will suffice for the number of mind changes in approximating $\Phi _0(A_0;x)$ , provided that $\mathcal {B}^1_0,\ldots ,\mathcal {B}^1_{n-1}$ are not injured.

What happens if $\mathcal {B}^1_{n-1}$ is injured? This will potentially cause $R^1_{n-1}$ to increase to, say, $R^1_{n-1}[s_2]>R^1_{n-1}[s_1]$ , which means that the number of injuries to $\Phi _0(A_0;x)$ will now be bounded by $R^1_{n-1}[s_2]>R^1_{n-1}[s_1]$ . This means that the ordinal bound for the injuries to $\Phi _0(A_0;x)$ will have to be larger than $\omega $ . $\mathcal {B}^1_{n-1}$ can be injured if a number $a_s<R^0_{n-1}[s_1]$ enters A, and each time $\mathcal {B}^1_{n-1}$ is injured, the ordinal bound for the number of injuries to $\Phi _0(A_0;x)$ will have to be increased. Thus, assuming that $\mathcal {B}^0_0,\ldots ,\mathcal {B}^0_{n-1}$ are never injured, the ordinal bound for the number of injuries to $\Phi _0(A_0;x)$ can be set as $\omega \cdot R^0_{n-1}[s_1]$ .

The reader should now be able to observe a pattern. With a fixed assignment of triples to blocks (as in Sacks splitting theorem), we see that the bound $\omega \cdot R^0_{n-1}[s_1]$ will have to be revised if $\mathcal {B}^0_{n-1}$ is injured by preserving $A_1\upharpoonright R^1_{n-2}$ . Thus, the straightforward bound is $\omega ^{\omega }$ .

In order to get a better bound, we will need to have a dynamic assignment of triples to blocks. Coming back to our example above, the action that had caused us to go beyond $\omega ^2$ is the injury to $\mathcal {B}^0_{n-1}$ , which allowed $R^0_{n-1}$ to increase past its original value of $R^0_{n-1}[s_1]$ . The solution is to combine all the blocks $\mathcal {B}^0_{n-1},\mathcal {B}^0_{n},\mathcal {B}^0_{n+1},\ldots $ whenever $\mathcal {B}^0_{n-1}$ is injured so that every triple $(0,y,0)$ introduced into the construction after $s_1-1$ is now in $\mathcal {B}^0_{n-1}$ . For instance, when $\mathcal {B}^0_{n-1}$ is injured after stage $s_1$ and $R^0_{n-1}$ is increased beyond $R^0_{n-1}[s_1]$ , we would transfer $(0,x,0)$ from $\mathcal {B}^0_n$ to $\mathcal {B}^0_{n-1}$ . Now the current restraint held by $\mathcal {B}^0_{n-2}$ is still $R^0_{n-2}[s_1]$ (otherwise we would have already transferred $(0,x,0)$ to $\mathcal {B}^0_{n-2}$ ), and so the original bound of $\omega \cdot R^0_{n-1}[s_1]>\omega \cdot R^0_{n-2}[s_1]$ will still work for $\Phi _0(A_0;x)$ . Obviously, if $\mathcal {B}^0_{n-2}$ is later initialized and $R^0_{n-2}$ is increased beyond $R^0_{n-2}[s_1]$ , we will transfer $(0,x,0)$ to $\mathcal {B}^0_{n-2}$ .

To finish off this example, we also need to verify that the ordinal bound for $\mathcal {B}^1_{n-1}$ is met despite the blocks $\mathcal {B}^0_{n-1},\mathcal {B}^0_{n},\mathcal {B}^0_{n+1},\ldots $ blocks being combined. The bound for $\mathcal {B}^1_{n-1}$ is declared to be $\omega \cdot R^1_{n-2}[t]$ where $t<s_1$ is the stage where we added a triple $(0,z,1)$ to $\mathcal {B}^1_{n-1}$ . If the situation described above happens, that is, if $\mathcal {B}^0_{n-1}$ is injured due to a small number less than $R^1_{n-2}[t]$ enters A, and the blocks $\mathcal {B}^0_{n-1},\mathcal {B}^0_{n},\mathcal {B}^0_{n+1},\ldots $ blocks are combined, we will be allowed to reset the number of mind changes for $\mathcal {B}^1_{n-1}$ as the bound was declared to be $\omega \cdot R^1_{n-2}[t]$ .

It is easy to see that under this revised strategy, we can have $\omega ^2$ as the bound for the number of injuries to $\Phi _0(A_0)$ and $\Phi _0(A_1)$ . Each block is initialized only finitely often and has a stable state with finitely many triples. Thus, if there is only a single $\Phi $ on each side, we will have no additional difficulties.

The main difficulty in this proof comes from considering multiple $\Phi $ s on each side. For instance, let us consider $\Phi _0(A_0)$ , $\Phi _1(A_0)$ , and $\Phi _0(A_1)$ , so that $0$ -blocks contain triples of the form $(0,x,0)$ and $(1,x',0)$ , and $1$ -blocks contain triples of the form $(0,x",1)$ . Suppose that both $\Phi _0(A_0)$ and $\Phi _1(A_0)$ are total, but the totality of $\Phi _1(A_0)$ is revealed much faster than that of $\Phi _0(A_0)$ . Let n be the least such that $\mathcal {B}^0_n$ currently does not contain any triple $(0,x,0)$ for $x>x_0$ . This scenario will occur if $\Phi _0(A_0;x_0+1)$ is not currently convergent and so $R^0_n$ will have to be computed without using $\Phi _0(A_0)$ . Assume also that $\Phi _1(A_0)$ is currently looking total. We will have to fill the blocks $\mathcal {B}^0_n,\mathcal {B}^0_{n+1},\ldots $ with $(1,x',0)$ triples, since it could be that $\Phi _1(A_0)$ is total but $\Phi _0(A_0)$ is not. Once a triple $(1,x_1,0)$ is initially put into $\mathcal {B}^0_{n+1}$ at some stage $s_1$ , the ordinal bound of $\omega \cdot R^0_n[s_1]$ will be declared (and cannot be increased later if we want $\Phi _1(A_0)$ to be $\omega ^2$ -c.a.) If $\Phi _0(A_0;x_0+1)$ later converges, we will have to put $(0,x_0+1,0)$ into $\mathcal {B}^0_n$ , the first $0$ -block not containing a $(0,x,0)$ -triple (the reason why we add $(0,x_0+1,0)$ to the smallest possible $0$ -block rather than a fresh $0$ -block is explained in the next paragraph). Unfortunately doing so will increase $R^0_n$ beyond $R^0_n[s_1]$ and so the bound previously declared for $(1,x_1,0)\in \mathcal {B}^0_{n+1}$ will be too small and will have to be increased. A quick calculation shows that a bound of $\omega ^3$ will suffice without modifying the above strategy.

The reader might wonder why we do not just add $(0,x_0+1,0)$ to $\mathcal {B}^0_N$ , where $\mathcal {B}^0_N$ is the first block of type $0$ not yet considered by the construction, when $\Phi _0(A_0;x_0+1)$ finally does converge. The reason is due to possible injury. Suppose that $(0,x_0+1,0)$ was (for the very first time) added to $\mathcal {B}^0_n$ . At that stage $u_0$ , we would have declared the bound for $(0,x_0+1,0)$ to be $\omega \cdot R^0_{n-1}[u_0]$ . However it could be that after $u_0$ there was an injury to the block $\mathcal {B}^0_n$ which caused the computation $\Phi _0(A_0;x_0+1)$ to be made undefined. As described above, we would have to (re-)fill the blocks $\mathcal {B}^0_n,\mathcal {B}^0_{n+1},\ldots $ with $(1,x',0)$ triples while waiting for $\Phi _0(A_0;x_0+1)$ to reconverge, and when it finally does, we do not want to add $(0,x_0+1,0)$ to the newest block $\mathcal {B}^0_N$ as the previously declared bound of $\omega \cdot R^0_{n-1}[u_0]$ will not be met at that block. Therefore we would want to return $(0,x_0+1,0)$ to its original block $\mathcal {B}^0_n$ . We also note that the very first time we add a triple $(0,x_0+1,0)$ to $\mathcal {B}^0_n$ we can choose n to be fresh, as we have not yet recorded its ordinal bound. However for easy bookkeeping we will always choose n as small as possible.

To overcome the problem above, the straightforward solution is to combine the elements in the blocks $\mathcal {B}^0_n,\mathcal {B}^0_{n+1},\ldots $ when $\Phi _0(A_0,x_0+1)$ converges and $(0,x_0+1,0)$ is added to $\mathcal {B}^0_n$ . In this way, the triple $(1,x_1,0)$ will be transferred from $\mathcal {B}^0_{n+1}$ to $\mathcal {B}^0_n$ when $(0,x_0+1,0)$ is added to $\mathcal {B}^0_n$ . Since we assumed that $R^0_{n-1}[s_1]$ already includes the use of a convergent $\Phi _0(A_0;x_0)[s_1]$ , it will never be increased again later due to $\Phi _0(A_0)$ looking total, and therefore the previously declared bound of $\omega \cdot R^0_n[s_1]>\omega \cdot R^0_{n-1}[s_1]$ for $\Phi _1(A_0;x_1)$ will still work after transferring $(1,x_1,0)$ to $\mathcal {B}^0_n$ . The motif here is to transfer all triples from $\cup _{k\geq n}\mathcal {B}^0_k$ into $\mathcal {B}^0_n$ whenever $R^0_n$ increases. This can happen when either $\mathcal {B}^0_n$ is injured or when we see $\Phi (A_0)$ convergence.

Unfortunately, the straightforward solution given above does not solve the problem completely, and there are further subtleties to be considered. The problematic case is when $\Phi _0(A_0)$ and $\Phi _1(A_0)$ are both total, but the totality of each functional alternates between being quickly and slowly revealed. Recall the definition of $\mathtt {Conv}\left (\mathcal {B}^0_n\right )$ from the previous section. Let’s consider a scenario where $\mathtt {Conv}\left (\mathcal {B}^0_k\right )\supset \infty \infty $ for all $k<n$ , and where $\mathtt {Conv}\left (\mathcal {B}^0_n\right )\supset f\infty $ . Then while waiting for $\Phi _0(A_0;x_0+1)$ to converge, we will have to add $(1,x_1,0)$ to $\mathcal {B}^0_{n+1}$ for some large $x_1$ . This can later be injured due to elements entering $A_0$ , so that when $\Phi _0(A_0;x_0+1)$ finally converges later and $(0,x_0+1,0)$ is added to $\mathcal {B}^0_n$ , we will have to transfer all triples in lower priority blocks into $\mathcal {B}^0_n$ . Unfortunately at this time, it could be that $\Phi _1(A_0;x_1)$ is currently undefined. This means that when $\Phi _1(A_0;x_1)$ later converges, the restraint $R^0_n$ of the block $\mathcal {B}^0_n$ will have to be increased. However, $\Phi _1(A_0;x_1)$ can now take a very long time to converge again, and in the meantime, $\Phi _0(A_0)$ will look total. This means that we must add $(0,x_2,0)$ to the block $\mathcal {B}^0_{n+1}$ for large $x_2$ , as $\Phi _0(A_0)$ cannot afford to wait for $\Phi _1(A_0;x_1)$ to re-converge. Now when $\Phi _1(A_0;x_1)$ finally converges again, $R^0_n$ will increase further, which means that $(0,x_2,0)$ will have to be transferred to $\mathcal {B}^0_n$ , during which $\Phi _0(A_0;x_2)$ may be undefined. The functionals $\Phi _0(A_0)$ and $\Phi _1(A_0)$ can alternate between quickly converging and slowly converging, so that in the end, we are forced to transfer almost every $(0,x,0)$ and $(1,x',0)$ to $\mathcal {B}^0_n$ , making the block infinite.

To arrange for blocks to be finite, we will need to allow for infinite injury between the requirement approximating $\Phi _0(A_0)$ and the requirement approximating $\Phi _1(A_0)$ . In order to get this to work we will need to have two different versions of the requirement approximating $\Phi _1(A_0)$ ; one that believes that $\Phi _0(A_0)$ is total (and hence $\mathtt {Conv}\left (\mathcal {B}^0_k\right )(0)=\infty $ for all k), and a second version that believes that $\Phi _0(A_0)$ is not total (and hence $\mathtt {Conv}\left (\mathcal {B}^0_k\right )(0)=f$ for cofinitely many k). The first version will delay defining the bound for $\Phi _1(A_0)$ on a block $\mathcal {B}^0_k$ until $\Phi _0(A_0)$ has shown itself to be total in the block, i.e., $\mathtt {Conv}\left (\mathcal {B}^0_k\right )(0)=\infty $ . The second version will work only with the blocks $\mathcal {B}^0_k$ where $\mathtt {Conv}\left (\mathcal {B}^0_k\right )(0)=f$ , and is initialized each time $\Phi _0(A_0)$ looks total. The actions of these different versions will be organized by keeping track of $\mathtt {Conv}\left (\mathcal {B}^0_k\right )$ . For instance, in the situation described in the previous paragraph, when $\Phi _0(A_0;x_0+1)$ is currently undefined, all triples of the form $(1,x_1,0)$ added to $\mathcal {B}^0_{n+1}$ are under the belief that $\Phi _0$ is not total. Later when $\Phi _0(A_0;x_0+1)$ converges and $R^0_n$ increases, we will simply initialize $\mathcal {B}^0_{n+1}$ and not transfer those triples $(1,x',0)$ to $\mathcal {B}^0_n$ . This allows us to break the feedback described above and ensure that each block is eventually finite. There are no additional difficulties beyond certain technical details which will be addressed in the formal construction.

3.2.1 Construction

We initially set all blocks to be empty. At stage $s>0$ , we do the following:

1. (I) For each $i=0,1$ , we do the following. Let n be the least such that $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s]>\delta _i[s]$ . Initialize $\mathcal {B}^i_k$ for all $k\geq n$ . For each $e\leq n$ such that $\delta _i[s](e)=\infty $ and for each triple $(e,x,i)$ that is not currently in any block, where $x<l(e,i)[s]$ , we put $(e,x,i)$ into $\mathcal {B}^i_n$ . We say that we act for $\mathcal {B}^i_n$ . If n does not exist, do nothing at this step.

2. (II) Let $\mathcal {B}^i_n$ be the highest priority block such that $a_s<R^i_n$ . Enumerate $a_s$ into $A_{1-i}$ , and initialize $\mathcal {B}^{1-i}_m$ for all m such that $\mathcal {B}^{1-i}_m>\mathcal {B}^i_n$ . If $\mathcal {B}^i_n$ does not exist, enumerate $a_s$ into $A_0$ .

3.2.2 Verification

Obviously, $A_0, A_1$ is a set splitting of A. We now verify that $A_0$ and $A_1$ have totally $\omega ^2$ -c.a. degrees. First of all, we observe that for any triple $(e,x,i)$ , any stage s, and any block $\mathcal {B}^i_n$ , if $(e,x,i)\in \mathcal {B}^i_n[s]$ then $\Phi _e(A_i;x)[s]\downarrow $ . Furthermore, for any $i, n,m,s$ , if $n<m$ then $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s]<\mathtt {Conv}\left (\mathcal {B}^i_m\right )[s]$ or $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s]\subset \mathtt {Conv}\left (\mathcal {B}^i_m\right )[s]$ .

Lemma 3.2. Suppose that we act for $\mathcal {B}^i_n$ at stage s. Then $\mathtt {Conv}\left (\mathcal {B}^i_n\right )\subseteq \delta _i[s]$ immediately after the action.

Proof Suppose not. Then there is a least $e\leq n$ such that $\mathtt {Conv}\left (\mathcal {B}^i_n\right )(e)=f$ and $\delta _i[s](e)=\infty $ . This means that there is some $k<n$ such that $(e,x,i)\in \mathcal {B}^i_k[s]$ , where $x=l(e,i)[s]-1$ . Let $t<s$ be the greatest stage where we acted for $\mathcal {B}^i_k$ and added $(e,x,i)$ to $\mathcal {B}^i_k$ . At stage t we must have $\delta _i[t]<\mathtt {Conv}\left (\mathcal {B}^i_k\right )[t+1]$ or $\delta _i[t]\supseteq \mathtt {Conv}\left (\mathcal {B}^i_k\right )[t+1]$ . By the maximality of t, we have $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[t+1]=\mathtt {Conv}\left (\mathcal {B}^i_k\right )[s]$ , and since we chose to act for $\mathcal {B}^i_n$ rather than $\mathcal {B}^i_k$ at stage s, it means that $\delta _i[s]\not <\mathtt {Conv}\left (\mathcal {B}^i_k\right )[s]$ , which must mean that $\delta _i[t]\upharpoonright e+1\leq \delta _i[s]\upharpoonright e+1$ . Since $\delta _i[s](e)=\infty $ , this must mean that $l(e,i)[s]>t>x$ , a contradiction.

Lemma 3.3. Each block is initialized at only finitely many stages.

Proof If $l(0,0)>0$ at some stage $s>0$ , then $\mathcal {B}^0_0=\{(0,x,0)\mid x<l(0,0)\}$ forever, otherwise $\mathcal {B}^0_0=\emptyset $ forever. So, $\mathcal {B}^0_0$ is initialized at most once. Now suppose that all blocks of priority higher than $\mathcal {B}^i_n$ are no longer initialized after stage s. Then we have $r^{i'}_k[t]=r^{i'}_k[s]$ for every $t>s$ and every block $\mathcal {B}^{i'}_k<\mathcal {B}^i_n$ . This means that $\mathcal {B}^i_n$ can be initialized under step (II) only finitely often after stage s.

Suppose that $\mathcal {B}^i_n$ is initialized under step (I) infinitely often. Pick the least e such that there are infinitely many stages $t>s$ where $\delta _i[t]\upharpoonright e=\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t]\upharpoonright e$ and $\delta _i[t](e)=\infty $ and $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t](e)=f$ . By the minimality of e, we see that $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t](e')$ is eventually stable for every $e'<e$ . Now let $t_1>t_0>s$ be two stages such that $\delta _i[t_k]\upharpoonright e=\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t_k]\upharpoonright e$ and $\delta _i[t_k](e)=\infty $ and $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t_k](e)=f$ for $k=0,1$ . Since we can assume that $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t_0]\upharpoonright e=\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t_1]\upharpoonright e$ , we see that $\delta _i[t_0]\upharpoonright e=\delta _i[t_1]\upharpoonright e$ and therefore $l(e,i)[t_1]>t_0$ , and thus $\left (e,t_0,i\right )$ will be added to $\mathcal {B}^i_n$ under step (I) at stage $t_1$ .

We now argue that $\left (e,t_0,i\right )$ will be in $\mathcal {B}^i_n[t]$ for every $t> t_1$ . Suppose $\left (e,t_0,i\right )$ is removed from $\mathcal {B}^i_n$ by the action at some stage $t_2>t_1$ . This must be under Step (I); however, since $\left (e,t_0,i\right )\in \mathcal {B}^i_n[t_2]$ , we have $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t_2]\upharpoonright e+1=\left (\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t_1]\upharpoonright e\right )\widehat {\phantom {\eta }} \infty $ . By the minimality of e, $\delta _i[t_2]$ cannot be to the left of $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t_1]\upharpoonright e$ , since $\delta _i[t_2]$ must be to the left of $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t_2]$ , it follows that $\delta _i[t_2](e)=\infty $ , and therefore $t_0<l(e,i)[t_2]$ . But this means that we would put $(e,t_0,i)$ back into $\mathcal {B}^i_n$ under Step (I) during stage $t_2$ , so that $\left (e,t_0,i\right )\in \mathcal {B}^i_n[t_2+1]$ . Thus, $\left (e,t_0,i\right )\in \mathcal {B}^i_n[t]$ for every $t> t_1$ . This means that $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[t](e)=\infty $ for almost every t, which contradicts the assumption on e.

Let $\hat {\delta }_i=\liminf _s\delta _i[s]$ . We will show that $A_0$ and $A_1$ have totally $\omega ^2$ -c.a. degree. We fix e and i such that $\Phi _e(A_i)$ is total, and let $s_0$ be a stage large enough so that $\forall t\geq s_0$ , $\delta _i[t]\upharpoonright e+1\geq \hat {\delta }_i\upharpoonright e+1$ , and that the blocks $\mathcal {B}^i_0,\ldots ,\mathcal {B}^i_{e}$ are never again initialized after $s_0$ . By checking the definition of $\delta _i$ , we can see easily that $\hat {\delta }_i(e)=\infty $ .

Lemma 3.4. For every $n>s_0$ , $\lim _s\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s]\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ .

Proof Fix $n>s_0$ . By Lemma 3.2, each time we act for $\mathcal {B}^i_n$ under Step (I), we will make $\mathtt {Conv}\left (\mathcal {B}^i_n\right )\upharpoonright e+1\geq \hat {\delta }_i\upharpoonright e+1$ . By Lemma 3.3, $\lim _s\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s]\upharpoonright e+1$ exists. Suppose for a contradiction that $\lim _s\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s]\upharpoonright e+1>\hat {\delta }_i\upharpoonright e+1$ . But this means that we will infinitely often act for $\mathcal {B}^i_n$ under Step (I), a contradiction.

The task for the rest of this proof is to define computable functions $\psi (x,s), c_0(x,s)$ and $c_1(x,s)$ so that for every x, $\lim _s\psi (x,s)=\Phi _e(A_i;x)$ and for every $x,s$ , we have $\omega \cdot c_0(x,s)+c_1(x,s)\geq \omega \cdot c_0(x,s+1)+c_1(x,s+1)$ and $\psi (x,s)\neq \psi (x,s+1)\Rightarrow \omega \cdot c_0(x,s)+c_1(x,s)> \omega \cdot c_0(x,s+1)+c_1(x,s+1)$ .

For the rest of this proof we fix an x large enough such that $(e,x,i)$ is never in $\cup _{j\leq s_0}\mathcal {B}^i_j$ (by Lemma 3.3 there are cofinitely many such x). Let $n_x[s]$ be the number n such that $(e,x,i)\in \mathcal {B}^i_{n}[s]$ and where $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s]\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ . If n cannot be found let $n_x[s]\uparrow $ .

Lemma 3.5. There are infinitely many s such that $n_x[s]\downarrow $ .

Proof Fix an arbitrarily large stage s such that $l(e,i)[s]>x$ , and the construction acts for $\mathcal {B}^i_n$ for some $n>s_0$ , and where $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[s]\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ for all k with $s_0<k<n$ . We also assume that $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s+1]\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ . This stage s can be found since $\lim _sl(e,i)[s]=\infty $ and by applying Lemma 3.4.

When acting for $\mathcal {B}^i_n$ at stage s, we cannot have $(e,x,i)\in \mathcal {B}^i_k[s]$ for any $k\leq s_0$ by the assumption on the largeness of x. If $(e,x,i)\in \mathcal {B}^i_k[s]$ for any $s_0<k<n$ then we have $n_x[s]\downarrow =k$ . Otherwise, the construction will be able to add $(e,x,i)$ to $\mathcal {B}^i_n$ in Step (I), and since $\mathcal {B}^i_n$ is not initialized in Step (II), we have $n_x[s+1]\downarrow =n$ .

We let $s_1\geq s_0$ be the first stage where $n_x[s_1]\downarrow $ and where there is some $s_1^{\prime }$ such that $\delta _i[s_1^{\prime }]\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ and $x<s_1^{\prime }<s_1$ . The stage $s_1$ exists by Lemma 3.5. Obviously, $n_x[s]\geq e$ for every s where it is defined.

Lemma 3.6. For every $t>s'>s_1$ , and n, if $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s']\upharpoonright e+1>\hat {\delta }_i\upharpoonright e+1$ and $(e,x,i)$ is not in any block at the beginning of stage $s'$ , and $t>s'$ is the least such that $n_x[t]\downarrow $ , we will have $n_x[t]\leq n$ .

Proof We can assume, without loss of generality, that there is no stage v and no $m\leq n$ such that $s'<v<t$ , $\mathtt {Conv}\left (\mathcal {B}^i_m\right )[v]\upharpoonright e+1>\hat {\delta }_i\upharpoonright e+1$ , and $(e,x,i)$ is not in any block at the beginning of stage v.

Now let $s"$ be the least stage such that $s"\geq s'$ and $\delta _i[s"]\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ .

Claim 3.7. For any stage $s"'$ and k with $s'\leq s"'\leq s"$ and $(e,x,i)\in \mathcal {B}^i_k[s"']$ we must have $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[s"']\upharpoonright e+1>\hat {\delta }_i\upharpoonright e+1$ .

Proof If $s"'$ exists then $s"'>s'$ and we can therefore assume that $s">s'$ as well. Note that $(e,x,i)$ must be added to $\mathcal {B}^i_k$ at some maximal stage v such that $s'\leq v <s"'$ ; this same action will cause $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[v+1]\upharpoonright e+1=\delta _i[v]\upharpoonright e+1$ (by Lemma 3.2). Since v is maximal, we have $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[v+1]\upharpoonright e+1=\mathtt {Conv}\left (\mathcal {B}^i_k\right )[s"']\upharpoonright e+1$ , and since $s'\leq v< s"'\leq s"$ , we also have $\delta _i[v]\upharpoonright e+1> \hat {\delta }_i\upharpoonright e+1$ by the minimality of $s"$ .

We now claim that $s"+1=t$ . Claim 3.7 tells us that $t\geq s"+1$ . We now verify that $n_x[s"+1]\downarrow $ , which will imply that $s"+1\geq t$ . Since we have $\mathtt {Conv}\left (\mathcal {B}^i_{n}\right )[s']\upharpoonright e+1>\hat {\delta }_i\upharpoonright e+1$ , by the minimality of $s"$ , we have $\delta _i[s"]<\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s"]$ . Thus the construction will act for $\mathcal {B}^i_m$ at stage $s"$ , for some $m\leq n$ . Since $s">s_0$ we must have $m>e$ . Since $\delta _i[s"](e)=\hat {\delta }_i(e)=\infty $ , we conclude that $l(e,i)[s"]>s_1^{\prime }>x$ . Therefore, when acting for $\mathcal {B}^i_m$ at stage $s"$ , we will add $(e,x,i)$ to $\mathcal {B}^i_m$ , unless $(e,x,i)\in \mathcal {B}^i_k[s"]$ for some $k<m$ . If this is the case, then by Claim 3.7, we must have $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[s"]\upharpoonright e+1>\hat {\delta }_i\upharpoonright e+1=\delta _i[s"]\upharpoonright e+1$ ; which means that we would have acted for $\mathcal {B}^i_k$ instead of $\mathcal {B}^i_m$ at stage $s"$ , a contradiction.

This contradiction shows that when acting for $\mathcal {B}^i_m$ at stage $s"$ we will successfully add $(e,x,i)$ to $\mathcal {B}^i_m$ . We will not initialize $\mathcal {B}^i_m$ in Step (II) at stage $s"$ by the assumption on $s'$ in the first line of this proof. By Lemma 3.2 we have $\mathtt {Conv}\left (\mathcal {B}^i_m\right )[s"+1]\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ . So therefore, we conclude that $t=s"+1$ and $n_x[t]=m\leq n$ .

Lemma 3.8. For every $t>s\geq s_1$ , if $n_x[t]\downarrow $ and $n_x[s]\downarrow $ then $n_x[t]\leq n_x[s]$ .

Proof Fix $t>s\geq s_1$ such that $n_x[t]\downarrow $ and $n_x[s]\downarrow $ . Let $n=n_x[s]$ . We may clearly assume that $\mathcal {B}^i_{n}$ is initialized at some least stage $s'$ such that $s\leq s'<t$ . We also assume that t is the least stage greater than $s'$ such that $n_x[t]\downarrow $ . By the minimality of $s'$ we have $\mathtt {Conv}\left (\mathcal {B}^i_{n}\right )[s']\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ . There are three possibilities for what might happen at stage $s'$ .

First, suppose that at stage $s'$ we did not act for $\mathcal {B}^i_m$ for any $m\leq n$ . This means that $\mathcal {B}^i_n$ did not get initialized in Step (I), but was initialized in Step (II). Thus, $\mathtt {Conv}\left (\mathcal {B}^i_n\right )[s'+1]=f^{n+1}$ and $(e,x,i)$ will not be in any block at the beginning of stage $s'+1$ , so apply Lemma 3.6 to conclude that $n_x[t]\leq n=n_x[s]$ .

Second, suppose that at stage $s'$ we acted for $\mathcal {B}^i_m$ for some $m\leq n$ , which is then initialized under Step (II). In that case, regardless of whether $(e,x,i)$ is transferred to $\mathcal {B}^i_m$ during Step (I), we will still have $\mathtt {Conv}\left (\mathcal {B}^i_m\right )[s'+1]=f^{m+1}$ and $(e,x,i)$ is not in any block at the beginning of stage $s'+1$ , so we can still apply Lemma 3.6 to conclude that $n_x[t]\leq m\leq n =n_x[s]$ .

Lastly, suppose that at stage $s'$ we acted for $\mathcal {B}^i_m$ for some $m\leq n$ , and $\mathcal {B}^i_m$ is not initialized under Step (II). Since $m\leq n$ , we see that $\mathtt {Conv}\left (\mathcal {B}^i_m\right )[s']\upharpoonright e+1\leq \mathtt {Conv}\left (\mathcal {B}^i_n\right )[s']\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ . Since we acted for $\mathcal {B}^i_m$ at $s'$ , we must have $\delta _i[s']\supseteq \hat {\delta }_i\upharpoonright e+1$ . Now since $\delta _i[s'](e)=\hat {\delta }_i(e)=\infty $ , we conclude that $l(e,i)[s']>s_1^{\prime }>x$ . This means that while acting for $\mathcal {B}^i_m$ at stage $s'$ , we will put $(e,x,i)$ into $\mathcal {B}^i_m$ . Since $\mathcal {B}^i_m$ is not initialized in Step (II), again, by Lemma 3.2, we have $t=s'+1$ , and $n_x[t]=m\leq n=n_x[s]$ .

We next show that after stage $s_1$ , all i-blocks of priority higher than $\mathcal {B}^i_{n_x}$ must be holding the original restraint from stage $s_1$ :

Lemma 3.9. For every $s\geq s_1$ such that $n_x[s]\downarrow $ , and every $k<n_x[s]$ , $R^i_{k}[s]=R^i_k[s_1]$ .

Proof Fix $s\geq s_1$ such that $n_x[s]\downarrow $ and some $k<n_x[s]$ such that $R^i_{k}[s]\neq R^i_k[s_1]$ . This means that there is some stage u such that $s_1\leq u<s$ and $\mathcal {B}^i_k$ is initialized at stage u. We fix the least $k<n_x[s]$ which is initialized at some such u, and for this k, we fix the largest u. If $\mathcal {B}^i_k$ is initialized in Step (II) at stage u, then $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[u+1]\upharpoonright e+1=f^{k+1}$ . By the minimality of k, $(e,x,i)$ is not in any block at the beginning of stage $u+1$ , so we can apply Lemma 3.6 and Lemma 3.8 to conclude that $n_x[s]\leq k$ , a contradiction. Thus we can assume that $\mathcal {B}^i_k$ is not initialized by step (II) at stage u.

In Step (I) of stage u, if we had acted for some $\mathcal {B}^i_{k'}$ for $k'<k$ , then regardless of whether we added $(e,x,i)$ to $\mathcal {B}^i_{k'}$ we cannot have $(e,x,i)\in \mathcal {B}^i_{k'}[u+1]$ by the minimality of k. Hence $(e,x,i)$ cannot be in any block at the beginning of stage $u+1$ , and so we can apply Lemma 3.6 again, together with Lemma 3.8 to conclude that $n_x[s]\leq k$ , a contradiction. Thus, we assume that we had acted for $\mathcal {B}^i_k$ in Step (I) of stage u.

Suppose for a contradiction that $\delta _i[u]\upharpoonright e+1=\hat {\delta }_i\upharpoonright e+1$ . Since $u\geq s_1>s_1^{\prime }>x$ , and since $\delta _i[u](e)=\infty $ , we conclude that $l(e,i)[u]>s_1^{\prime }>x$ . Since we assume that $\mathcal {B}^i_0,\ldots ,\mathcal {B}^i_e$ are already stable, we have $e<k$ . As $(e,x,i)$ cannot be in $\mathcal {B}^i_{k'}[u]$ for any $k'<k$ , we will add $(e,x,i)$ to $\mathcal {B}^i_k$ during Step (I). Since $\mathcal {B}^i_k$ is not initialized by Step (II), we conclude that $(e,x,i)\in \mathcal {B}^i_k[u+1]$ , contradicting the maximality of u.

This contradiction says that $\delta _i[u]\upharpoonright e+1>\hat {\delta }_i\upharpoonright e+1$ . By Lemma 3.2 and the fact that $\mathcal {B}^i_k$ is not initialized in Step (II), we see that $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[u+1]\upharpoonright e+1>\hat {\delta }_i\upharpoonright e+1$ . Again, $(e,x,i)$ cannot be in any block at the beginning of stage $u+1$ , otherwise it must be in $\mathcal {B}^i_{k}[u+1]$ , contradicting the maximality of u. Apply Lemma 3.6 and Lemma 3.8 again to conclude that $n_x[s]\leq k$ , a contradiction.

Now we are ready to define $c_0(x,s), c_1(x,s)$ and $\psi (x,s)$ . Let $Q^i_k[s]=$ number of elements $x<R^i_k[s]$ such that $x\not \in A[s]$ , and define $Q^{1-i}_k[s]$ similarly. We define $Q^{i}_{-1}[s]=Q^{1-i}_{-1}[s]=0$ . For $s<s_1$ we define $c_1(x,s)=\psi (x,s)=0$ , and $c_0(x,s)=n_0\cdot R^i_{n_0-1}[s_1]\cdot 2^{(n_0+1)^2}$ , where $n_0=n_x[s_1]$ . If $s\geq s_1$ and $n_x[s]\uparrow $ then we define $c_0(x,s)=c_0(x,s-1)$ , $c_1(x,s)=c_1(x,s-1)$ and $\psi (x,s)=\psi (x,s-1)$ . Now suppose that $s\geq s_1$ and $n_x[s]\downarrow =n$ . Let m be the largest such that $\mathcal {B}^{1-i}_m<\mathcal {B}^i_n$ (so that $m=n$ if $i=1$ and $m=n-1$ if $i=0$ ). We update according to the following rules:

• • Set $c_1(x,s)=Q^{1-i}_m[s]$ .

• • Set $\psi (x,s)=\Phi _e(A_i;x)[t]$ where $t\geq s$ is the least such that $n_x[t]\downarrow $ and $\Phi _e(A_i;x)[t]\downarrow $ .

• • Decrease $c_0(x,s)$ by $1$ if $s>s_1$ and one of the following holds:

  1. – $c_1(x,s)>c_1(x,s')$ ,

  2. – $n_x[s]<n_x[s']$ , or

  3. – $\mathcal {B}^{1-i}_m$ is initialized at some stage u with $s'\leq u<s$ ,

  where $s'<s$ is the largest such that $n_x[s']\downarrow $ . Otherwise, keep $c_0(x,s)=c_0(x,s-1)$ .

We will only care about the values of $c_0(x,s),c_1(x,s)$ , and $\psi (x,s)$ for $s\geq s_1$ . Notice that $s_0$ is fixed for $\Phi _e(A_i)$ , and $s_1$ can be found effectively in x. Therefore, $|c_0|,c_1$ , and $\psi $ are computable functions. Note that $\psi $ is total since $\Phi _e(A_i)$ is total.

Clearly, $\lim _{s\geq s_1}\psi (x,s)=\Phi _e(A_i;x)$ by Lemma 3.5.

Lemma 3.10. For any $s\geq s_1$ , if $\psi (x,s)\neq \psi (x,s+1)$ then either $c_0(x,s)\neq c_0(x,s+1)$ or $c_1(x,s)\neq c_1(x,s+1)$ .

Proof Let $s\geq s_1$ and let $s'$ be largest such that $s_1\leq s'\leq s$ and $n=n_x[s']\downarrow $ . We may also assume that $n_x[s+1]\downarrow $ , and by Lemma 3.8, $n\geq n_x[s+1]$ . Let’s suppose for a contradiction that $c_0(x,s)=c_0(x,s+1)$ and $c_1(x,s)=c_1(x,s+1)$ . This implies that $n_x[s+1]=n_x[s']=n$ , $\mathcal {B}^{1-i}_m$ is not initialized at any stage u with $s'\leq u\leq s$ , and $Q^{1-i}_m[s+1]=Q^{1-i}_m[s']$ . Notice that if $i=0$ and $n=0$ then $\mathcal {B}^{1-i}_m$ is not defined, but the same argument below still holds.

We now consider different cases. First, suppose that $\mathcal {B}^i_n$ is initialized in Step (II) at some stage u where $s'\leq u\leq s$ . Then this means that $a_u<R^{1-i}_m[u]=R^{1-i}_m[s']$ (since $\mathcal {B}^i_m$ is not initialized), which in turn means that $Q^{1-i}_m[s']\neq Q^{1-i}_m[s+1]$ , contrary to one of our assumptions. So this first scenario is impossible.

Second, suppose we act for $\mathcal {B}^i_k$ at some stage u where $s'\leq u\leq s$ and some $k<n$ . Fix k with the least corresponding u. By the minimality of u, we must have $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[u]\upharpoonright e+1=\mathtt {Conv}\left (\mathcal {B}^i_k\right )[s']\upharpoonright e+1\leq \mathtt {Conv}\left (\mathcal {B}^i_n\right )[s']\upharpoonright e+1= \hat {\delta }_i\upharpoonright e+1$ . Since we acted for $\mathcal {B}^i_k$ at stage u, we must have $\delta _i[u]\supset \hat {\delta }_i\upharpoonright e+1$ , which implies that $(e,x,i)$ must be put into $\mathcal {B}^i_k$ by this action. Since $\mathcal {B}^i_k$ isn’t initialized in Step (II) of stage u (otherwise the first scenario above holds), this implies that $(e,x,i)\in \mathcal {B}^i_k[u+1]$ , which means that $n_x[u+1]\downarrow =k<n$ . Since $u+1\leq s+1$ , this contradicts Lemma 3.8. So this second scenario is also impossible.

Third, suppose we act for $\mathcal {B}^i_n$ at some stage u where $s'\leq u\leq s$ . Then the same argument as for the second scenario tells us that $u=s$ (by the maximality of $s'$ ), and after acting for $\mathcal {B}^i_n$ at stage $u=s$ , we will also put $(e,x,i)$ back into $\mathcal {B}^i_n$ .

We conclude that if $\mathcal {B}^i_n$ is initialized between $s'$ and s, it can only be in Step (I) of stage s, where this action will also put $(e,x,i)$ into $\mathcal {B}^i_n$ . This means that in Step (II) of every stage between $s'$ and s, we have $(e,x,i)\in \mathcal {B}^i_n$ . Since $\psi (x,s+1)\neq \psi (x,s')$ , we must have $\Phi _e(A_i;x)[s']\downarrow $ , and hence there must be some least stage t such that $s'\leq t\leq s$ and $a_t$ is enumerated into $A_i$ by Step (II) of the construction at stage t, where $a_t$ is below the use of $\Phi _e(A_i;x)[s']$ . But during Step (II) of stage t, we have $(e,x,i)\in \mathcal {B}^i_n$ , which means that $a_t<R^{1-i}_m[s']$ , which in turn means that $Q^{1-i}_m[s']\neq Q^{1-i}_m[s+1]$ , contradicting one of our assumptions. Thus we conclude that either $c_0(x,s)\neq c_0(x,s+1)$ or $c_1(x,s)\neq c_1(x,s+1)$ .

Lemma 3.11. For every s, $c_0(x,s)\geq 0$ .

Proof Suppose that $s'$ and s are two stages such that $s_1\leq s'<s+1$ , $n=n_x[s']=n_x[s+1]$ and where $A[s']\upharpoonright R^i_{n_0-1}[s_1]=A[s+1]\upharpoonright R^i_{n_0-1}[s_1]$ and $s'\leq s$ is the largest such that $n_x[s']\downarrow $ . Suppose that $c_0(x,s')\neq c_0(x,s+1)$ . If $\mathcal {B}^{1-i}_m$ is initialized under Step (II) at some stage u with $s'\leq u\leq s$ , then $a_u<R^{i}_{n-1}[u]=R^i_{n-1}[s_1]$ , by Lemma 3.9, contrary to the assumptions. On the other hand, if $\mathcal {B}^{1-i}_m$ is not initialized at any stage u with $s'\leq u\leq s$ then obviously $R^{1-i}_m[s']=R^{1-i}_m[s+1]$ and so $Q^{1-i}_m[s']\geq Q^{1-i}_m[s+1]$ , which means that $c_0(x,s')= c_0(x,s+1)$ , a contradiction. Hence $\mathcal {B}^i_m$ is initialized under Step (I) at some stage u where $s'\leq u\leq s$ . Since $\mathcal {B}^i_m$ is initialized under Step (I) but never under Step (II) between $s'$ and s, we see that $\mathtt {Conv}\left (\mathcal {B}^i_k\right )[s']> \mathtt {Conv}\left (\mathcal {B}^i_k\right )[s+1]$ for the least $k\leq m$ such that $\mathcal {B}^i_k$ is acted on between $s'$ and s.

This says that so long as $n_x[s]$ and $A[s]\upharpoonright R^i_{n_0-1}[s_1]$ do not change, the value of $c_0(x,s)$ can decrease at most $2\cdot 2^2\cdots 2^{(m+1)}<2^{(n_0+1)^2}$ many times. Since $c_0(x,s_1)=n_0\cdot R^i_{n_0-1}[s_1]\cdot 2^{(n_0+1)^2}$ , we conclude that $c_0(x,s)\geq 0$ for every s.

This concludes the proof of Theorem 3.1.

4 Unbounded type

Theorem 4.1. Let $\alpha < \varepsilon _0$ . There are a c.e. set A and a noncomputable c.e. set C, such that if $A=A_0\sqcup A_{1}$ is a c.e. splitting of A, and $A_{0}$ is totally $\alpha $ -c.a. then $C\le _T A_{1}$ .

Before we give the proof of the theorem, we first isolate the property of totally $\alpha $ -c.a. sets to be used, where we call a total computable function $f: \omega \times \omega \to \omega $ a computable convergent approximation if, for any $x \geq 0$ , $\lim _{s \to \infty } f(x,s) < \omega $ exists.

Lemma 4.2. Let $\alpha < \varepsilon _0$ . There is a uniformly computable sequence of computable convergent approximations $\{f_i\}_{i \geq 0}$ such that, for any total $\alpha $ -c.a. function g there is an index i such that $f_i$ converges to g, i.e., $g(x) = \lim _{s \to \infty } f_i(x,s)$ for all numbers $x \geq 0$ .

Proof In order to avoid technicalities, we give the proof for $\alpha = \omega ^2$ . The general case is obtained by a similar argument using the fact that any ordinal $\alpha < \varepsilon _0$ has an effective Cantor normal form (see Reference).

Call a triple $(f,k,p)$ of total computable functions of type $\omega \times \omega \to \omega $ a computable $\omega ^2$ -approximation (of g) if (f converges to g and), for any numbers x and s, the following hold.

1. (i) If $f(x,s+1) \not = f(x,s)$ then $(k(x,s+1),p(x,s+1)) \not = (k(x,s),p(x,s))$ , and

2. (ii) if $(k(x,s+1),p(x,s+1)) \not = (k(x,s),p(x,s))$ then either $k(x,s+1) < k(x,s)$ or $k(x,s+1) = k(x,s)$ and $p(x,s+1) < p(x,s)$ .

By viewing $k(x,s)$ and $p(x,s)$ as the coefficients of the Cantor normal form of the ordinal $o(x,s) = k(x,s) \cdot \omega + p(x,s) < \omega ^2$ , the functions k and p assign an ordinal $o(x,s) < \omega ^2$ to each value $f(x,s)$ such that whenever $f(x,s)$ changes, i.e., $f(x,s+1) \not = f(x,s)$ , then the corresponding ordinal decreases, i.e., $o(x,s+1) < o(x,s)$ . So f is a convergent approximation and, by definition, a function g is $\omega ^2$ -c.a. if and only if there is a computable $\omega ^2$ -approximation $(f,k,p)$ of g. Moreover, given a computable $\omega ^2$ -approximation $(f,k,p)$ of a function g, by slowing down the approximation we obtain a primitive recursive $\omega ^2$ -approximation of g, i.e., a computable $\omega ^2$ -approximation $(\hat {f},\hat {k},\hat {p})$ of g where the functions $\hat {f},\hat {k},\hat {p}$ are primitive recursive (see Reference). Finally, since there is a computable numbering of the primitive recursive functions, we easily obtain a computable sequence $\{({f}_i, {k}_i, {p}_i)\}_{i \geq 0}$ of all primitive recursive $\omega ^2$ -approximations. So, by dropping the parameters ${k}_i$ and ${p}_i$ , this gives the desired computable sequence $\{f_i\}_{i \geq 0}$ of computable convergent approximations providing approximations of all total $\omega ^2$ -c.a. functions.

Proof of Theorem 4.1

We construct the desired c.e. sets A and C by a tree argument. It suffices to meet the noncomputability requirements

$$ \begin{align*}P_n:\overline{C}\ne W_n\end{align*} $$

and the (global) splitting requirements

$$ \begin{align*}R^{global}_{e}: \text{ If } X_e \cup Y_e=A \text{ and } X_e \text{ is totally } \alpha\text{-c.a. then } C \le_T Y_e \end{align*} $$

for $n \geq 0$ and $e \geq 0$ , respectively, where $\{(X_e,Y_e)\}_{e \geq 0}$ is a computable numbering of all disjoint pairs of c.e. sets.

In order to meet the global requirement $R^{global}_{e}$ we define a total function $g_e \leq _T X_e$ and ensure that $C \le _T Y_e$ provided that $X_e \cup Y_e=A$ and $g_e$ is $\alpha $ -c.a. In fact, since this task is too complex to be handled directly, we break it up into the local splitting requirements

$$ \begin{align*} R_{\langle e, i \rangle}: \text{ If } X_e \cup Y_e=A \text{ and if } f_i \text{ converges to } g_e \text{ then } C \le_T Y_e \end{align*} $$

( $i \geq 0$ ) where $\{f_i\}_{i \geq 0}$ is a computable sequence of computable convergent approximations as in Lemma 4.2.

Here the reduction $C\leq _T Y_e$ will be ensured via delayed simple permitting. During the construction we will ensure that for all but finitely many y, if $Y_e\upharpoonright y$ is stable at s then $C\upharpoonright y$ is stable at $\theta (s)$ for a computable function $\theta $ . This delay is due to the working of the priority tree and also the need to synchronize between different R requirements. This will be discussed below in detail.

Let $A_s$ and $C_s$ be the finite parts of A and C, respectively, enumerated by the end of stage s (where $A_0=C_0=\emptyset $ ), and fix uniformly computable enumerations $\{X_{e,s}\}_{s \geq 0}$ and $\{Y_{e,s}\}_{s \geq 0}$ of the c.e. sets $X_e$ and $Y_e$ , respectively ( $e \geq 0$ ). We define uniformly computable approximations $g_e(z)[s]$ of the functions $g_e$ ( $e \geq 0$ ), where $g_e(z)[s]$ is the value of $g_e(z)$ at the end of stage s, and where we obey the following rules (for $e,z,s \geq 0$ ).

1. (g₀) $g_e(z)[s] = z$ for $s \leq z$ .

2. (g₁) If $g_e(z)[s+1] \not = g_e(z)[s]$ then $X_{e,s+1} \upharpoonright g_e(z)[s]+1 \not = X_{e,s} \upharpoonright g_e(z)[s]+1$ .

3. (g₂) If $g_e(z)[s+1] \not = g_e(z)[s]$ then $g_e(z)[s+1] =s+1$ (hence $g_e(z)[s] < g_e(z)[s+1]$ .

4. (g₃) There are at most finitely many s such that $g_e(z)[s+1] \not = g_e(z)[s]$ .

So, intuitively, we may view $g_e(z)$ as (the final position of) a movable marker, where $g_e(z)[s]$ is the position of the marker at the end of stage s. The marker $g_e(z)$ is moved only finitely often ((g $_3$ )), it is not moved prior to stage $z+1$ , and its initial position is z ((g $_0$ )), and if it is moved then it is moved to a higher position, namely the current stage ((g $_2$ )), and the move is permitted by a change of $X_e$ at or below the current position ((g $_1$ )). So, obviously, the rules for defining $g_e(z)[s]$ guarantee that, $g_e(z)[s]$ is nondecreasing in s, $g_e(z)[s] \geq z$ and, for $s \geq z$ , $g_e(z)[s] \leq s$ , $g_e(z) = \lim _{s \to \infty } g_e(z)[s] < \omega $ exists for all $z \geq 0$ , and $g_e \leq _T X_e$ ( $e \geq 0$ ). (In the construction below we tacitly assume that, for $s \leq z$ , $g_e(z)[s]$ is defined according to (g $_0$ ), and that $g_e(z)[s+1] = g_e(z)[s]$ unless explicitly stated otherwise.)

We call a splitting requirement $R_{\langle e, i \rangle }$ infinitary if its premises are correct, i.e., if $X_e \cup Y_e =A$ and $\lim _{s} f_i(z,s) = g_e(z)$ for all numbers z, and we call $R_{\langle e, i \rangle }$ finitary otherwise. The priority tree of the construction is the full binary tree $T = \{0,1\}^{< \omega }$ . A node (i.e., binary string) $\alpha $ of length n codes a guess which of the first n R-requirements are infinitary, where $\alpha (m)=0$ denotes that $R_m$ is infinitary and $\alpha (m)=1$ denotes that $R_m$ is finitary ( $m <n$ ). At the end of any stage s of the construction we define a string $\delta _s$ of length s as follows, where $\delta _s$ is the guess at the type of the first s splitting requirements $R_0, \dots , R_{s-1}$ with which we work at stage $s+1$ .

First, define the length function $\ell $ by letting $\ell (\langle e, i \rangle ,s)$ be the greatest $\ell \leq s$ such that

$$ \begin{align*}\forall \; z < \ell \; (g_e(z)[s] = f_i(z,s) \; \& \; A_s \upharpoonright g_e(z)[s]+1 = (X_{e,s} \cup Y_{e,s}) \upharpoonright g_e(z)[s]+1).\end{align*} $$

Since, for any number z, $\lim _{s \to \infty } g_e(z)[s] < \omega $ and $\lim _{s \to \infty } f_i(z,s)< \omega $ exist (by construction of $g_e$ and by choice of $f_i$ , respectively), it follows that $\lim _{s \to \infty } \ell (\langle e, i \rangle ,s) = \omega $ if $R_{\langle e, i \rangle }$ is infinitary, and $\lim _{s \to \infty } \ell (\langle e, i \rangle ,s) < \omega $ otherwise. (For the construction it will be crucial that, for infinitary $R_{\langle e, i \rangle }$ and for any numbers y and z such that $y \leq g_e(z)[s]$ and $z < \ell (\langle e, i \rangle ,s)$ where $y \not \in A_s$ , it holds that $y \not \in X_{e,s} \cup Y_{e,s}$ and, by enumerating y into A at stage $s+1$ we can force y to enter either $X_e$ or $Y_e$ at a stage $\geq s+1$ .)

Next, for each node $\alpha $ , inductively define $\alpha $ -stages as follows. Each stage $s\geq 0$ is a $\lambda $ -stage. If s is an $\alpha $ -stage and if $\ell (|\alpha |,s)>\ell (|\alpha |,t)$ for all $\alpha $ -stages $t<s$ , then call s $\alpha $ -expansionary. Then an $\alpha $ -stage s is an $\alpha 0$ -stage if s is $\alpha $ -expansionary and s is an $\alpha 1$ -stage otherwise.

Finally, for any $s \geq 0$ , let $\delta _s \in T$ be the unique node $\alpha $ of length s such that s is an $\alpha $ -stage (and call a node $\beta $ accessible at stage $s+1$ if $\beta \sqsubseteq \delta _s$ ), and let $\delta $ be the left most path through T, such that, for any number $m \geq 0$ , $\delta \upharpoonright m \sqsubset \delta _s$ for infinitely many stages s. The path $\delta $ is the true path through T, i.e., for any $m \geq 0$ , $\delta (m) = 0$ if and only if the splitting requirement $R_m$ is infinitary. This fact, to which we refer as the True Path Lemma in the following, is proved by a straightforward induction on m using the above observations on the length function $\ell $ .

For each node $\beta $ of length n there is a strategy $P_{\beta }$ for meeting the noncomputability requirement $P_n$ which is based on the guess that a higher priority R-requirement $R_m$ $(m < n)$ is infinitary iff $\beta (m) = 0$ . (For notational convenience, we call $R_m$ —as well as m and $\beta \upharpoonright m$ — $\beta $ -infinitary if $\beta (m)=0$ and $\beta $ -finitary otherwise ( $m < |\beta |$ ). So, for $\beta = \delta \upharpoonright n$ , $R_m$ is $\beta $ -infinitary iff $R_m$ is infinitary.) We will guarantee that the strategy $P_{\beta }$ on the true path, $\beta = \delta \upharpoonright n$ , meets the requirement $P_n$ .

Before we explain the strategies $P_{\beta }$ , we make some general remarks on the format of the construction. The strategies $P_{\beta }$ are finitary. Numbers are enumerated into the sets A and C under construction only by these strategies. At any stage $s+1> 0$ there is a unique $\beta $ such that $P_{\beta }$ becomes active at stage $s+1$ , and, for this $\beta $ , $\beta \leq \delta _s$ , i.e., either $\beta $ is to the left of $\delta _s$ ( $\beta <_L \delta _s$ ) or $\beta $ is an initial segment of $\delta _s$ ( $\beta \sqsubseteq \delta _s$ ). Moreover, if $P_{\beta }$ acts at stage $s+1$ then all strategies $P_{\beta '}$ with $\beta < \beta '$ are initialized at stage $s+1$ . (So, in particular, all strategies to the right of the true path $\delta $ are initialized infinitely often.) Finally, if $P_{\beta }$ is in its initial state at stage s and acts at stage $s+1$ then $\beta $ is accessible at stage $s+1$ and $P_{\beta }$ may enumerate only numbers $\geq s+1$ into A or C at any later stage. (For technical convenience, we let this first action be vacuous and start with the proper actions for the sake of $P_n$ only afterwards.) Note that this framework ensure that any strategy $P_{\beta }$ with $\beta \sqsubset \delta $ is initialized only finitely often, and, in order to ensure that an infinitary splitting requirement $R_{\langle e,i \rangle }$ is met, it suffices to ensure that $Y_e$ can compute the numbers enumerated into C by strategies $P_{\beta }$ with $(\delta \upharpoonright \langle e,i \rangle )0 = \delta \upharpoonright (\langle e,i \rangle +1) \sqsubseteq \beta $ .

The strategy $P_{\beta }$ ( $|\beta |=n$ ) is a refinement of the usual noncomputability strategy: at some stage $s+1$ , appoint $x = s+1$ as follower. Then wait for a stage $s' \geq s$ such that $x \in W_{n,s'}$ , i.e., such that the follower x is realized at stage $s'$ (and all larger stages). If there is such a stage $s'$ then enumerate x into C at stage $s'+1$ , and keep x out of C otherwise. (Followers will be the only numbers which may be enumerated into C.)

Now, if $\langle e,i \rangle < n$ is $\beta $ -infinitary then the strategy $P_{\beta }$ has to ensure that the set $Y_e$ “knows” whether or not the follower x is put into C (provided that $(\beta \upharpoonright \langle e,i \rangle )0 \sqsubset \delta $ ). (If there is no $\beta $ -infinitary R-requirement then $P_{\beta }$ is just the basic strategy and we call $P_{\beta }$ trivial.) If $R_{\langle e,i \rangle }$ , $\langle e,i \rangle < n$ , is the unique $\beta $ -infinitary requirement of higher priority then this can be achieved by the following basic module. First, at some stage $s+1$ , we appoint an unused number $z \geq s+1$ as tracker and an unused number $y \geq s+1$ such that $y \leq g_e(z)[s]$ as agitator. (For simplicity, by (g $_0$ ), we let $z = s+1$ and $y= g_e(z)[s]=g_e(s+1)[s]=s+1$ .) Next, at any stage $s'+1> s+1$ , we appoint an unused number $x \geq g_e(z)[s] (=g_e(z)[s'])$ as follower (for simplicity, we let $s'=s+1$ and $x = s'+1 = s+2$ ). Now, if there is a stage $s">s'$ such that x is realized at stage $s"$ then we further wait for a stage $s"'> s"$ such that $\ell (\langle e,i \rangle ,s"') \geq z$ . (We say, we wait for confirmation. Note that, for $x \in W_n$ , such a stage $s"'$ must exist if $\beta $ is on the true path $\delta $ , i.e., if $P_{\beta }$ ’s guess that $R_{\langle e,i \rangle }$ is infinitary is correct.) Then $y \leq g_e(z)[s"'] \leq x$ (since, for the tracker z, $g_e(z)$ may be changed only by $P_{\beta }$ hence $g_e(z)[s"'] = g_e(z)[s]$ ) and

$$ \begin{align*}g_e(z)[s"'] = f_i(z,s"') \; \& \; A_{s"'} \upharpoonright g_e(z)[s"']+1 = (X_{e,s"'} \cup Y_{e,s"'}) \upharpoonright g_e(z)[s"']+1).\end{align*} $$

So enumerating the agitator y into A at stage $s"'+1$ forces y to enter either $X_{e}$ or $Y_{e}$ at a stage $>s"'$ (still assuming $\beta \sqsubseteq \delta $ ). If $s""$ is the least stage $> s"'$ at which this happens and $Y_e(y)$ changes then, by $y \leq x$ , this permits the enumeration of the follower x into C thereby meeting $P_n$ (recall that $C\leq _T Y_e$ via the identity use). Otherwise, the enumeration of $y \leq g_e(z)[s"']$ into $X_e$ allows us to redefine $g_e(z)$ at stage $s""+1$ . In this case, we replace the agitator and the follower by new unused numbers $y'$ and $x'$ , respectively, adjust the value of $g_e(z)[s""+1]$ in such a way that $y' \leq g_e(z)[s""+1] \leq x'$ (for simplicity, at stage $s""+1$ we let $y' = g_e(z)[s""+1] = s""+1$ and at stage $s""+2$ we let $x'=s""+2$ ), and iterate the above process for the parameters $z, y', x'$ . Note that, though we have replaced the agitator and follower, the tracker z is fixed. Since at any stage $t+1$ at which we raise the value of $g_e(z)$ there has been a lesser stage $t'$ such that $g_e(z)[t] = g_e(z)[t'] = f_i(z,t')$ , this process must stop after finitely many rounds since any change of $g_e(z)[t]$ is mirrored by a change of $f_i(z,t)$ , and $f_i$ is a convergent approximation. So (assuming $\beta \sqsubseteq \delta $ ), eventually, there will be a follower which either is never realized or is realized and put into C whence $P_n$ is met. So the above action of the strategy $P_{\beta }$ for $P_n$ is finitary, and—assuming $\beta \sqsubset \delta $ —it ensures that $P_n$ is met.

If there is more than one $\beta $ -infinitary R-requirement then some synchronization is needed. While in the basic module the required reduction of C to $Y_e$ is obtained by direct permitting, in the general case we achieve this by delayed permitting. In order to demonstrate this we consider the case of two $\beta $ -infinitary R-requirements, say $R_{\langle e_0,i_0 \rangle }$ and $R_{\langle e_1,i_1 \rangle }$ where $\langle e_0,i_0 \rangle < \langle e_1,i_1 \rangle $ (and where $\alpha _0$ and $\alpha _1$ are the corresponding nodes expanded by $\beta $ , i.e., $\alpha _0 0 \sqsubset \alpha _1 0 \sqsubseteq \beta $ ). There will be a 0-module related to $R_{\langle e_0,i_0 \rangle }$ and a 1-module related to $R_{\langle e_1,i_1 \rangle }$ . We start by appointing a $0$ -tracker $z_{0}$ and a $0$ -agitator $y_{0}$ (corresponding to $\langle e_0,i_0 \rangle $ ), a $1$ -tracker $z_{1}$ and a $1$ -agitator $y_{1}$ (corresponding to $\langle e_1,i_1 \rangle $ ), and a (common) follower x with the required properties as in the basic module where we have to ensure that all numbers are unused and the parameters for $\alpha _0$ differ from the corresponding parameters for $\alpha _1$ (for simplicity, at some stage $s+1$ we let $z_0 = s+1$ and $y_0 = g_{e_0}(z_0)[s]=s+1$ , at stage $s+2$ we let $z_1= s+2$ and $y_1 = g_{e_1}(z_1)[s+1]=s+2$ , and at stage $s+3$ we let $x = s+3$ ). Then we start the basic module for $\langle e_1,i_1 \rangle $ , i.e., the $1$ -module, with the parameters $z_1, y_1,x$ , which involves waiting for x to be confirmed and enumerating the agitator $y_1$ . Now it may happen that there will be a stage $s'$ such that the current follower $x[s']$ is permitted by $Y_{e_1}$ to enter C at stage $s'+1$ (if this is not the case and $\beta \sqsubset \delta $ then, as in the basic module, we may argue that $P_n$ is met). Now, at stage $s'+1$ , instead of enumerating $x[s']$ into C, we activate the basic module for $\langle e_0,i_0\rangle $ , i.e., the 0-module, with the previously defined agitator and tracker and the current follower (note that $x[s+2] \leq x[s']$ ), wait for getting (0-)confirmation, if so enumerate $y_0$ into A, and wait for the corresponding change of $X_{e_0}$ or $Y_{e_0}$ (say at stage $s"$ ; note that, assuming that $\alpha _0 0 \sqsubset \delta $ , such a stage must exist). Now, if $Y_{e_0}$ permits $x[s']$ , then the attack is completed by enumerating $x[s']$ into C. Otherwise, i.e., if $X_{e_0}$ allows us to raise the value of $g_{e_0}(z_0)$ , then—as in the basic module—we replace the $0$ -agitator and raise the value of $g_{e_0}(z_0)$ at stage $s"+1$ (by setting $y_0[s"+1] = g_{e_0}(z_0)[s"+1] = s"+1$ ) and, at the next stages, we reset the parameters of the 1-module including the follower (by setting $z_1[s"+2] = s"+2$ , $y_{1}[s"+2] = g_{e_1}(s"+2)[s"+2]$ and $x[s"+3]=s"+3$ ) and start the basic module for $\langle e_1, i_1\rangle $ with these new parameters.

As in the basic module we may argue that any instance of the $1$ -module is finite and (assuming $\beta \sqsubset \delta $ ) either guarantees that $P_n$ is met as witnessed by the current follower or ends with a call of the $0$ -module. Since the tracker $z_0$ of the 0-module is fixed, we may argue—again, as in the basic module—that this module is finite and (assuming $\beta \sqsubset \delta $ ) either ends with the current follower witnessing that $P_n$ is met or with the call of a final instance of the 1-module where the follower of this instance witnesses that $P_n$ is met. So the strategy is finitary and, assuming $\beta \sqsubset \delta $ , the strategy ensures that $P_n$ is met. Moreover, as in the basic module, the action is compatible with $R_{\langle e_0,i_0 \rangle }$ since the follower x is put into C only if it is permitted by $Y_{e_0}$ . Compatibility with $R_{\langle e_1,i_1 \rangle }$ is by delayed permitting. To show the latter assume that $\alpha _10 \sqsubset \delta $ (otherwise the action of $P_{\beta }$ is not relevant for the satisfaction of the requirement $R_{\langle e_1,i_1 \rangle }$ as pointed out above). Then $\alpha _0 0 \sqsubset \delta $ whence $R_{\langle e_0,i_0 \rangle }$ is infinitary. So any call of the 0-module will result either in the enumeration of the current follower into C or in a reset of the 1-module entailing the cancellation of the follower (unless the strategy $P_{\beta }$ is initialized, in which case the follower is cancelled too). Since any call of the 0-module starts with the permitting of the current follower by $Y_{e_1}$ , this shows that $C \leq _T Y_{e_1}$ by delayed permitting.

To summarize the above discussion with two R requirements, we note the following: We keep running the basic strategy for the $1$ -module until we get a confirmed follower with permission from $Y_{e_1}$ to be enumerated into C. Then we run the $0$ -module strategy to see if that follower also gets permission from $Y_{e_0}$ ; if yes, that follower is fully cleared by both $Y_{e_0}$ and $Y_{e_1}$ and can be enumerated into C. If no, then we reset all parameters associated with the $1$ -module and repeat until we eventually get a fully cleared follower.

We now turn to the construction. There and in the following we use the following additional notation related to the noncomputability strategies $P_{\beta }$ . For any node $\beta $ let n be the length of $\beta $ (and, similarly, $|\beta '|=n'$ etc.). Let $m^{\beta }$ be the number of $\beta $ -infinitary R-requirements (hence $P_{\beta }$ is trivial if $m^{\beta } = 0$ ). If $P_{\beta }$ is not trivial, let

$$ \begin{align*}\langle e^{\beta}_0, i^{\beta}_0 \rangle < \dots < \langle e^{\beta}_{m^{\beta}-1}, i^{\beta}_{m^{\beta}-1} \rangle < n \; \text{ and } \; \alpha^{\beta}_0 \sqsubset \dots \sqsubset \alpha^{\beta}_{m^{\beta}-1} \sqsubset \beta \end{align*} $$

be the $\beta $ -infinitary numbers and $\beta $ -infinitary nodes in order of magnitude.

At any stage s of the construction the strategy $P_{\beta }$ will be in exactly one of the following states describing the progress of the current attack ( $m < m^{\beta }$ ): initial state, waiting for an m-tracker, waiting for a follower, waiting for realization, waiting for m-confirmation, waiting for m-permission, and being satisfied. The m-tracker, m-agitator, and follower of $\beta $ at the end of stage s (if defined) are denoted by $z^{\beta }_m[s]$ , $y^{\beta }_m[s]$ , and $x^{\beta }[s]$ , respectively, where the m-tracker and m-agitator are concerned with the $\beta $ -infinitary R-requirement $R_{\langle e^{\beta }_m, i^{\beta }_m \rangle }$ . (Moreover, the m-agitator $y^{\beta }_m[s]$ is defined at stage s iff the m-tracker $z^{\beta }_m[s]$ is defined at stage s and, if so, $y^{\beta }_m[s] = g_{e^{\beta }_m}(z^{\beta }_m[s])[s]$ . Hence, strictly speaking, $y^{\beta }_m[s]$ is redundant.) All parameters associated with $P_{\beta }$ persist unless they are explicitly changed. If $P_{\beta }$ becomes initialized then it is reset to the initial state and all numbers associated with it (if any) are cancelled.

1. Stage 0. For any $\beta $ , $P_{\beta }$ is initialized at stage $0$ , hence in the initial state.

2. Stage s+1. The highest priority strategy $P_{\beta }$ which requires attention at stage $s+1$ acts according to the case via which it requires attention as described in the following. All strategies $P_{\beta '}$ with $\beta < \beta '$ are initialized.

   The strategy $P_{\beta }$ requires attention at stage $s+1$ if one of the following holds (where $m < m^{\beta }$ ).

   1. (0) $P_{\beta }$ is in the initial state at the end of stage s and $\beta \sqsubseteq \delta _s$ .

      Action. If $P_{\beta }$ is trivial then declare that $P_{\beta }$ waits for a follower. If $P_{\beta }$ is not trivial then declare that $P_{\beta }$ waits for a $0$ -tracker.

   2. (1)_m $P_{\beta }$ waits for an m-tracker at the end of stage s.

      Action. Appoint $z^{\beta }_m[s+1] = s+1$ as m-tracker of $\beta $ , and call $y^{\beta }_m[s+1] = g_{e_m}(z^{\beta }_m[s+1])[s+1] (= g_{e_m}(s+1)[s+1]=s+1)$ the m-agitator of $\beta $ at stage $s+1$ . If $m < m^{\beta }-1$ declare that $P_{\beta }$ waits for an $(m+1)$ -tracker. Otherwise declare that $P_{\beta }$ waits for a follower.

   3. (2) $P_{\beta }$ waits for a follower at the end of stage s.

      Action. Appoint $x^{\beta }[s+1] = s+1$ as $\beta $ -follower and declare that $P_{\beta }$ waits for realization.

   4. (3) $P_{\beta }$ waits for realization at the end of stage s and $x^{\beta }[s] \in W_{n,s}$ .

      Action. If $P_{\beta }$ is trivial then enumerate $x^{\beta }[s]$ into C and declare that $P_{\beta }$ is satisfied. Otherwise declare that $P_{\beta }$ waits for $(m^{\beta }-1)$ -confirmation.

   5. (4)_m $P_{\beta }$ waits for m-confirmation at the end of stage s and $\ell (\langle e^{\beta }_m, i^{\beta }_m \rangle , s)> z^{\beta }_m[s]$ .

      Action. Enumerate the m-agitator $y^{\beta }_m[s]$ into A. Declare that $P_{\beta }$ waits for m-permission.

   6. (5)_m ^Y $P_{\beta }$ waits for m-permission at the end of stage s and $y^{\beta }_m[s] = g_{e^{\beta }_m}(z^{\beta }_m[s])[s]$ is in $Y_{e^{\beta }_m,s} \setminus Y_{e^{\beta }_m,s-1}$ .

      Action. If $m=0$ then enumerate $x^{\beta }[s]$ into C and declare that $P_{\beta }$ is satisfied. If $m> 0$ then declare that $P_{\beta }$ waits for $(m-1)$ -confirmation.

   7. (5)_m ^X $P_{\beta }$ waits for m-permission at the end of stage s and $y^{\beta }_m[s] = g_{e^{\beta }_m}(z^{\beta }_m[s])[s]$ is in $X_{e^{\beta }_m,s} \setminus X_{e^{\beta }_m,s-1}$ .

      Action. Let $g_{e^{\beta }_m}(z^{\beta }_m[s])[s+1] = s+1$ and replace the m-agitator of $\beta $ by $y^{\beta }_m[s+1]= g_{e^{\beta }_m}(z^{\beta }_m[s])[s+1] (= g_{e^{\beta }_m}(s+1)[s+1] =s+1)$ . If $m < m^{\beta }-1$ then, for $m < m' \leq m^{\beta }-1$ , cancel the current $m'$ -tracker and $m'$ -agitator of $\beta $ , cancel the current follower of $\beta $ , and declare that $P_{\beta }$ waits for an $(m+1)$ -tracker. Otherwise, cancel the current follower of $\beta $ and declare that $P_{\beta }$ waits for a follower.

   If $P_{\beta }$ acts via clause $(4)_m$ at stage $s+1$ then we say that $P_{\beta }$ m-acts at stage $s+1$ , if $P_{\beta }$ requires attention via $(5)^Y_m$ at stage $s+1$ then we say that $P_{\beta }$ is m-permitted at stage s, and if $P_{\beta }$ acts via $(5)^X_m$ at stage $s+1$ then we say that $P_{\beta }$ is m-reset at stage $s+1$ .

This completes the construction. In order to show that the construction is correct, we start with some observations.

The strategy $P_{\delta _s}$ requires attention via clause (0) at stage $s+1$ . So there is a unique node $\beta $ , in the following denoted by $\beta _s$ , such that the strategy $P_{\beta }$ becomes active at stage $s+1$ . Note that $\beta _s \leq \delta _s$ and all strategies $P_{\beta '}$ with $\beta _s < \beta '$ (hence with $\delta _s < \beta '$ ) are initialized at stage $s+1$ .

Next note that, at any stage $s+1$ , at most one tracker is appointed, and—if so—this tracker is assigned the value $s+1$ . So trackers are mutually different, i.e., if $(\beta ,m) \not = (\beta ',m')$ and $z^{\beta }_m[s]$ and $z^{\beta '}_{m'}[s']$ are defined then $z^{\beta }_m[s] \not =z^{\beta '}_{m'}[s']$ . Moreover, $z^{\beta }_m[s] \leq s$ and if $s < s'$ and $z^{\beta }_m[s] \downarrow \not = z^{\beta }_m[s'] \downarrow $ then $s < z^{\beta }_m[s']$ . Corresponding observations apply to agitators and followers, respectively. Also note that if $P_{\beta }$ acts via clause $(4)_m$ at stages $s+1 < s'+1$ then $y^{\beta }_m[s] < y^{\beta }_m[s']$ since there must be a stage $s"$ with $s+1 < s"+1 < s'+1$ such that $P_{\beta }$ is initialized or $m'$ -reset for some $m' \leq m$ at stage $s"+1$ whence $y^{\beta }_m[s] \leq s < s"+1 \leq y^{\beta }_m[s']$ . So a number new y is enumerated into A at stage $s+1$ (i.e., $y \in A_{s+1} \setminus A_s$ ) if and only if, for $\beta = \beta _s$ , $y= g_{e^{\beta }_m}(z^{\beta }_m[s],s)$ and $P_{\beta }$ acts via $(4)_m$ at stage $s+1$ . Similarly, a new number x is enumerated into C at stage $s+1$ iff, for $\beta = \beta _s$ , x is the follower $x^{\beta }[s]$ of the strategy $P_{\beta }$ at the end of stage s and either $P_{\beta }$ is trivial and acts via (3) at stage $s+1$ or $P_{\beta }$ is nontrivial and acts via $(5)^Y_0$ at stage $s+1$ .

Claim 1. (a) If $P_{\beta }$ is initialized only finitely often then $P_{\beta }$ requires attention only finitely often.

(b) If $\beta \sqsubset \delta $ then there is a stage $s_{\beta }$ such that no strategy $P_{\beta '}$ with $\beta ' <_L \beta $ requires attention after stage $s_{\beta }$ .

(c) If $\beta \sqsubset \delta $ then $P_{\beta }$ is initialized only finitely often and requires attention only finitely often.

Proof (a) Given $\beta $ , for a contradiction assume that $P_{\beta }$ is initialized only finitely often and $P_{\beta }$ requires attention infinitely often. Fix $t_0$ maximal such that $P_{\beta }$ is initialized at stage $t_0$ . Then $P_{\beta }$ acts at any stage $s+1> t_0$ at which it requires attention. So, in particular, $P_{\beta }$ acts infinitely often but is initialized only finitely often. As one can easily check, this implies that $P_{\beta }$ is nontrivial and $P_{\beta }$ is reset infinitely often. So fix $m < m^{\beta }$ minimal such that $P_{\beta }$ is m-reset infinitely often, fix $t_1> t_0$ minimal such that $P_{\beta }$ is not $m'$ -reset for any $m' < m$ after stage $t_1$ , and let $s_k +1$ ( $k \geq 0$ ) be the stages $> t_1$ at which $P_{\beta }$ is m-reset (where $s_k < s_{k+1}$ ). Then $P_{\beta }$ has an m-tracker at the end of stage $s_1$ , say $z = z^{\beta }_m[s_1]$ . Since $P_{\beta }$ is neither initialized nor $m'$ -reset for any $m' < m$ after this stage, this tracker is permanent, i.e., $z^{\beta }_m[s] = z$ for all stages $s \geq s_1$ . Since $P_{\beta }$ is m-reset at stage $s_k+1$ , it follows that $y^{\beta }_m[s_k+1]]= g_{e^{\beta }_m}(z)[s_k+1] = s_k+1$ for all $k \geq 1$ . In fact, since $s_{k+1}+1$ is the next greater stage at which $P_{\beta }$ is m-reset, it follows that $g_{e^{\beta }_m}(z)[s] = s_k+1$ for all stages s with $s_k+1 \leq s < s_{k+1}+1$ . On the other hand, by construction, there must be a stage $\hat {s}_k$ such that $s_k < \hat {s}_k < s_{k+1}$ and such that $P_{\beta }$ m-acts at stage $\hat {s}_k+1$ , i.e., acts via clause $(4)_m$ at stage $\hat {s}_k+1$ . Hence $\ell (\langle e^{\beta }_m, i^{\beta }_m), \hat {s}_k)> z$ , i.e., $f_{i^{\beta }_m}(z,\hat {s}_k) = g_{e^{\beta }_m}(z)[s] = s_k+1$ . So $\lim _{k \to \infty } f_{i^{\beta }_m}(z,\hat {s}_k) = \omega $ . But this contradicts the fact that $f_{i^{\beta }_m}$ is a convergent approximation, i.e., that $\lim _{s \to \infty } f_{i^{\beta }_m}(z,s) < \omega $ exists.

(b) Fix $\beta \sqsubset \delta $ . Since $\beta $ is on the true path, we may fix a stage t such that $\beta \leq \delta _s$ for $s \geq t$ . Then no strategy $P_{\beta '}$ with $\beta ' <_L \beta $ requires attention via clause (0) after stage t (since $\beta ' \not \sqsubseteq \delta _s$ ). So a strategy $P_{\beta '}$ with $\beta ' <_L \beta $ can require attention at a stage $s+1>t$ only if $P_{\beta '}$ has acted before stage $t+1$ and if $P_{\beta '}$ has not been initialized at any stage u with $t \leq u \leq s$ . Since there are only finitely many strategies which act prior to stage $t+1$ , the existence of the desired stage $s_{\beta }$ follows by part (a) of the claim.

(c) The proof is by induction on $|\beta |$ . Fix $\beta \sqsubset \delta $ and, by inductive hypothesis, fix $s_0> s_{\beta }$ such that no strategy $P_{\beta '}$ with $\beta ' \sqsubset \beta $ requires attention after stage $s_0$ (where $s_{\beta }$ is chosen as in part (b) of the claim). Then no strategy $P_{\beta '}$ with $\beta ' < \beta $ acts after stage $s_0$ . So $P_{\beta }$ is not initialized after stage $s_0$ . The second part of (c) follows by part (a) of the claim.

Claim 2. For $e \geq 0$ , $g_e$ is total and $g_e \leq _T X_e$ .

Proof Fix e and z. It suffices to show that $(g_0)$ – $(g_2)$ hold for all stages s and $(g_3)$ holds. $(g_0)$ is immediate. For a proof of $(g_1)$ and $(g_2)$ assume that $g_e(z)[s+1] \not = g_e(z)[s]$ . Then there is a unique nontrivial strategy $P_{\beta }$ and a number $m < m^{\beta }$ such that $e=e^{\beta }_m$ , $z = z^{\beta }_m[s]$ and $P_{\beta }$ acts via clause $(5)^X_m$ . So, by case assumption, $X_{e,s+1}(g_e(z)[s]) \not = X_{e,s}(g_e(z)[s])$ and $g_e(z)[s] < g_e(z)[s+1]$ since $g_e(z)[s] \leq s$ and $g_e(z)[s+1] = s+1$ .

Finally, for a proof of $(g_3)$ , for a contradiction assume that there are infinitely many stages s such that $g_e(z)[s+1] \not = g_e(z)[s]$ . Then there is a nontrivial strategy $P_{\beta }$ , a number $m < m^{\beta }$ , and a stage $s_0$ such that z becomes appointed as m-tracker of $\beta $ at stage $s_0+1$ , and there are infinitely many stages $s \geq s_0$ such that $z= z^{\beta }_m[s] = z^{\beta }_m[s_0+1]$ —whence $P_{\beta }$ is not initialized after stage $s_0$ —and $P_{\beta }$ acts via $(5)^X_m$ at stage $s+1$ . But this contradicts Claim 1(a). $\Box $

Claim 3. For $n \geq 0$ , $P_n$ is met.

Proof Fix $\beta $ such that $|\beta | = n$ and $\beta $ is on the true path $\delta $ . We will show that $P_{\beta }$ has a permanent follower x and that $x \in C$ iff $x \in W_n$ . So x witnesses that $P_n$ is met.

By Claim 1 fix $s_0$ minimal such that $P_{\beta }$ is not initialized after stage $s_0+1$ and $P_{\beta }$ does not require attention (hence does not act) after stage $s_0+1$ . Then the state $\sigma $ of $P_{\beta }$ at the end of stage $s_0+1$ is permanent and so are all other parameters associated with $P_{\beta }$ at the end of stage $s_0+1$ .

Obviously, $\sigma $ is not the initial state (otherwise, by $\beta \sqsubset \delta $ , there are infinitely many stages $s> s_0$ such that $\beta \sqsubseteq \delta _s$ and $P_{\beta }$ would require attention via (0) at stage $s+1$ for any such s). Similarly, $P_{\beta }$ cannot permanently wait for an m-tracker or a follower (since otherwise $P_{\beta }$ would require attention via $(1)_m$ or (2) at any stage $s+1> s_0+1$ ). So, by minimality of $s_0$ , $P_{\beta }$ acts at stage $s_0+1$ , has a follower x at this stage, and either $P_{\beta }$ is trivial or, for all $m \leq m^{\beta }-1$ , an m-tracker $z_m = z^{\beta }_m[s_0+1]$ and the corresponding m-agitator $y_m = y^{\beta }_m[s_0+1] = g_{e_m}(z_m)[s_0+1]$ are defined. Moreover, if $P_{\beta }$ permanently waits for realization or is permanently satisfied then, as one can easily check, $C(x)=W_n(x)=0$ and $C(x)=W_n(x)=1$ , respectively. So, in the remainder of the argument we may assume that $P_{\beta }$ is nontrivial, and it suffices to rule out that $P_{\beta }$ permanently waits for m-confirmation or permanently waits for m-permission for some $m < m^{\beta }$ .

For a contradiction, first assume that $P_{\beta }$ permanently waits for m-confirmation. Since $\alpha ^{\beta }_m0 \sqsubseteq \beta \sqsubset \delta $ , $\lim _{s \to \infty } \ell (\langle e^{\beta }_m,i^{\beta }_m \rangle ,s) = \omega $ , hence $\ell (\langle e^{\beta }_m,i^{\beta }_m \rangle ,s)> z_m$ for almost all $s \geq s_0+1$ . So $P_{\beta }$ will require attention via clause $(4)_m$ after stage $s_0+1$ . A contradiction.

Finally, assume that $P_{\beta }$ permanently waits for m-permission. Then $P_{\beta }$ acts via $(4)_m$ at stage $s_0+1$ . It follows that the parameters attached to $P_{\beta }$ are unchanged at stage $s_0+1$ and so is the approximation of $g_{e^{\beta }_m}$ . So the corresponding values are permanent, i.e., $z^{\beta }_m = z^{\beta }_m[s]$ and $y^{\beta }_m = y^{\beta }_m[s] = g_{e^{\beta }_m}(z^{\beta }_m[s])[s] = g_{e^{\beta }_m}(z^{\beta }_m)$ for all $s \geq s_0$ . Moreover, $y^{\beta }_m[s_0] \not \in A_{s_0}$ and $\ell (\langle e^{\beta }_m, i^{\beta }_m \rangle , s_0)>z^{\beta }_m[s_0]$ whence $A_{s_0}(y^{\beta }_m[s_0]) = X_{e^{\beta }_m,s_0}(y^{\beta }_m[s_0]) = Y_{e^{\beta }_ms_0}(y^{\beta }_m[s_0]) = 0$ , and $y^{\beta }_m[s_0]$ is enumerated into A at stage $s_0+1$ . Since, by $\alpha ^{\beta }_m0 \sqsubseteq \beta \sqsubset \delta $ , $A= X_{e^{\beta }_m} \cup Y_{e^{\beta }_m}$ , it follows that there must be a stage $s> s_0$ such that $y^{\beta }_m[s_0] = y^{\beta }_m[s]$ is enumerated into $X_{e^{\beta }_m}$ or $Y_{e^{\beta }_m}$ at stage $s+1$ . But this implies that $P_{\beta }$ requires attention via $(5)^X_m$ or $(5)^Y_m$ at stage $s+1> s_0+1$ contrary to the choice of $s_0$ .

This completes the proof of Claim 3. $\Box $

Claim 4. For $e,i \geq 0$ , $R_{\langle e,i \rangle }$ is met.

Proof Fix $e,i \geq 0$ where w.l.o.g. $R_{\langle e,i \rangle }$ is infinitary, i.e., $X_e \cup Y_e = A$ and $f_i$ converges to $g_e$ . Let $\alpha = \delta \upharpoonright \langle e,i \rangle $ . By assumption, $\delta (\langle e,i \rangle )=0$ , hence $\alpha 0 \sqsubset \delta $ . So, by Claim 1, we may fix a stage $s_0$ such that no strategy $P_{\beta }$ with $\beta < \alpha 0$ acts after stage $s_0$ .

Given a number x, we have to show that $C(x)$ can be computed from $Y_e$ uniformly in x. Note that x may be put into C only if x is a follower. Moreover, if x is a follower then $x> 0$ and x is appointed at stage x whence we may decide whether or not x is a follower. So, in the following, w.l.o.g. we may assume that x is a follower, we may let $s_x = x-1$ (so $s_x+1=x$ is the stage at which x is appointed), and we may fix the unique $\beta $ such that x follows $P_{\beta }$ . Distinguish the following three cases.

Case 1: $\beta < \alpha 0$ . Then, by case assumption and by choice of $s_0$ , x is in C if and only if x is enumerated into C by the end of stage $s_0$ .

Case 2: $\alpha 0 <_L \beta $ . By $\alpha 0 \sqsubset \delta $ , $\beta $ is to the right of $\delta $ whence $P_{\beta }$ is initialized infinitely often. So x is in C if and only if x is enumerated into C by the end of stage $t_x$ where $t_x$ is the least stage $> x = s_x+1$ at which $P_{\beta }$ is initialized.

Case 3: $\alpha 0 \sqsubset \beta $ . By case assumption, $\langle e,i \rangle $ is $\beta $ -infinitary (hence, in particular, $P_{\beta }$ is nontrivial) and we may (effectively) fix $m < m^{\beta }$ such that $\langle e,i \rangle = \langle e^{\beta }_m, i^{\beta }_m \rangle $ and $\alpha = \alpha ^{\beta }_m$ . Since x is appointed as $P_{\beta }$ -follower (i.e., $P_{\beta }$ acts via clause (2)) at stage $s_x+1 =x$ , it follows by construction that, for any $m' < m^{\beta }$ , $P_{\beta }$ has an $m'$ -tracker $z_{m'} = z^{\beta }_{m'}[s_x]$ at the end of stage $s_x$ and a corresponding $m'$ -agitator $y_{m'} = y^{\beta }_{m'}[s_x] = g_{e^{\beta }_{m'}}(z_{m'})[s_x]$ . Note that if any of this parameters changes at a stage $s+1> s_x$ then, at the least such stage $s+1$ , $P_{\beta }$ is reset or initialized hence x is cancelled. Moreover, if x is enumerated into C at a stage $s+1> s_x$ then there must be a stage $s'$ such that $s_x+1 < s'+1 \leq s+1$ and $P_{\beta }$ acts via clause $(5)^Y_m$ at stage $s'+1$ whence $y_m = y^{\beta }_m[s'] \in Y_{e,s'} \setminus Y_{e,s'-1}$ .

So, in the remainder of the argument, w.l.o.g. we may assume that $y_m \in Y_e$ (since $x \not \in C$ otherwise). It suffices to show that there is a stage $s+1> s_x+1$ such that the $P_{\beta }$ -follower x is cancelled at stage $s+1$ or x is enumerated into C at stage $s+1$ (whence $C(x)=C_{s+1}(x)$ for the least such stage s). For a contradiction assume that there is no such stage. Since x is never cancelled, $P_{\beta }$ is neither reset nor initialized after stage $s_x$ . So the parameters $z_{m'}$ , $y_{m'}$ , and x are permanent, i.e., $z^{\beta }_{m'}[s]=z_{m'}$ , $y^{\beta }_{m'}[s] = g_{e^{\beta }_{m'}}(z^{\beta }_{m'})[s] = g_{e^{\beta }_{m'}}(z_{m'})[s_x] = y_{m'}$ , and $x^{\beta }[s]=x$ for $s \geq s_x$ ( $m' < m^{\beta }$ ), $P_{\beta }$ acts whenever it requires attention after stage $s_x$ , and $P_{\beta }$ does not require attention via clause $(5)^X_{m'}$ ( $m' < m^{\beta }$ ) after this stage. Moreover, by Claim 1, there is a greatest stage $\geq s_x+1$ , say $t_0+1$ , at which $P_{\beta }$ requires attention. On the other hand, since $R_{\langle e,i \rangle }$ is infinitary and since the m-agitator $y_m$ of $P_{\beta }$ is in $Y_e$ , there must be a stage $s+1> s_x+1$ at which $P_{\beta }$ acts via $(4)_m$ and enumerates $y_m$ into A. So there must be a number $m^{\prime }_0 \leq m$ such that $P_{\beta }$ acts via $(4)_{m^{\prime }_0}$ or $(5)^Y_{m^{\prime }_0}$ at stage $t_0+1$ .

Now, it is crucial to note that, for any $m' \leq m$ , the requirement $R_{\langle e^{\beta }_{m'}, i^{\beta }_{m'} \rangle }$ is infinitary since $R_{\langle e^{\beta }_{m'}, i^{\beta }_{m'} \rangle }$ is $\beta $ -infinitary and $\langle e^{\beta }_{m'}, i^{\beta }_{m'} \rangle \leq \langle e^{\beta }_{m}, i^{\beta }_{m} \rangle $ whence $\alpha _{m'}0 \sqsubseteq \alpha _m0 \sqsubseteq \beta \upharpoonright \langle e^{\beta }_{m}, i^{\beta }_{m} \rangle +1 \sqsubset \delta $ . This gives the desired contradiction as follows. First assume that $P_{\beta }$ acts via $(5)^Y_{m^{\prime }_0}$ at stage $t_0+1$ . Since x is not enumerated into C, $m^{\prime }_0> 0$ and $P_{\beta }$ waits for $(m^{\prime }_0-1)$ -confirmation at all stages $s \geq t_0+1$ . Since $R_{\langle e^{\beta }_{m^{\prime }_0-1}, i^{\beta }_{m^{\prime }_0-1} \rangle }$ is infinitary, hence $\ell (\langle e^{\beta }_{m^{\prime }_0-1}, i^{\beta }_{m^{\prime }_0-1} \rangle , s)> z_{m^{\prime }_0-1}$ for almost all stages s, it follows that $P_{\beta }$ requires attention via $(4)_{m^{\prime }_0-1}$ after stage $t_0+1$ contrary to choice of $t_0$ . Finally, assume that $P_{\beta }$ acts via $(4)_{m^{\prime }_0}$ at stage $t_0+1$ . Then $\ell (\langle e^{\beta }_{m^{\prime }_0-1}, i^{\beta }_{m^{\prime }_0-1} \rangle , t_0)> z_{m^{\prime }_0-1}$ whence $A_{t_0}(y_{m^{\prime }_0-1}) = (X_{e^{\beta }_{m^{\prime }_0-1},t_0} \cup Y_{e^{\beta }_{m^{\prime }_0-1},t_0})(y_{m^{\prime }_0-1})=0$ , $y_{m^{\prime }_0-1}$ is enumerated into A at stage $t_0+1$ and $P_{\beta }$ waits for $(m^{\prime }_0-1)$ -permission at all stages $s \geq t_0+1$ . So, since $R_{\langle e^{\beta }_{m^{\prime }_0-1}, i^{\beta }_{m^{\prime }_0-1} \rangle }$ is infinitary, there is a stage $s \geq t_0+1$ such that $y_{m^{\prime }_0-1}$ is enumerated into $X_{e^{\beta }_{m^{\prime }_0-1}}$ or $Y_{e^{\beta }_{m^{\prime }_0-1}}$ at stage s. So $P_{\beta }$ requires attention via clause $(5)^Y_{m^{\prime }_0-1}$ or $(5)^X_{m^{\prime }_0-1}$ at stage $s+1> t_0+1$ contrary to choice of $t_0$ .

This completes the procedure for uniformly computing $C(x)$ from $Y_e$ and the proof of Claim 4. (Note that the reduction $C \leq _T Y_e$ is by delayed straight permitting, hence a wtt-reduction, in fact an ibT-reduction. So in the statement of Theorem 4.1 we may replace $C \leq _T A_1$ by $C \leq _{wtt} A_1$ or even $C \leq _{ibT} A_1$ .) $\Box $

Now, correctness of the construction is immediate by Claims 2–4. This completes the proof of the theorem.

Theorem 4.1 means that the strong version of Sacks’ Splitting Theorem is truly “finite injury of unbounded type.” As we point out in the introduction, the result also holds for degrees.

Theorem 4.3. Let $\alpha <\varepsilon _0$ . There are c.e. degrees $\mathbf {a}$ and $\mathbf c> \mathbf 0$ such that for all c.e. degrees $\mathbf {a}_0,\mathbf {a}_1$ with $\mathbf {a}_0 \lor \mathbf {a}_1=\mathbf {a}$ , if $\mathbf {a}_0$ is totally $\alpha $ -c.a. then $\mathbf c \le \mathbf {a}_1$ .

Proof (sketch)

The proof resembles the proof of Theorem 4.1 though it is somewhat more involved. We only sketch the necessary changes. The splitting requirements

$$ \begin{align*}R_{\langle e, i \rangle}: \text{ If } X_e \cup Y_e=A \text{ and if } f_i \text{ converges to } g_e \text{ then } C \le_T Y_e \end{align*} $$

in the set proof are replaced by

$$ \begin{align*}R_{\langle e, i \rangle}: \text{ If } \Phi_e^{X_e \cup Y_e}=A \text{ and } \Psi_e^A= X_e \cup Y_e \text{ and if } f_i \text{ converges to } g_e \text{ then } C \le_T Y_e, \end{align*} $$

where now $\{(X_e,Y_e,\Phi _e, \Psi _e)\}_{e \geq 0}$ is a computable numbering of all disjoint pairs of c.e. sets and all pairs of Turing functionals. ¹ The convergent approximations $f_i$ are chosen as in the previous proof, and, as there, the functions $g_e$ are total functions defined in the course of the construction. Moreover, if $\Phi _e^{X_e \cup Y_e}=A$ and $\Psi _e^A= X_e \cup Y_e$ —in the following we shortly say that e is correct—then $g_e$ is $X_e$ -computable (in the previous proof, $g_e$ was $X_e$ -computable for any e). It is easy to show that this together with meeting the noncomputability requirements and the modified splitting requirements gives the theorem for $\mathbf {a} = deg_T(A)$ and $\mathbf {c}=deg_T(C)$ .

As in the previous proof we define a length of agreement function $\ell (\langle e,i \rangle ,s)$ in order to guess whether $R_{\langle e,i \rangle }$ is infinitary (i.e., whether the hypotheses are correct) or not. For this sake we first define the length function $\hat {\ell }(e,s)$ corresponding to the first hypothesis (depending on e only) describing the current A-controllable length of agreement between A and $\Phi _e^{X_e \cup Y_e}$ . Let $\hat {\ell }(e,s)$ be the greatest $\ell \leq s$ such that

$$ \begin{align*}\forall \; y < \ell \; ( \Phi_{e,s}^{X_{e,s}\cup Y_{e,s}}(y)=A_s(y) \land \forall \; u < \varphi_{e,s}^{X_{e,s}\cup Y_{e,s}}(y)( \Psi_{e,s}^{A_s}(u) = X_{e,s} \cup Y_{e,s}(u))).\end{align*} $$

Then the length function $\ell $ is defined by

$$ \begin{align*}\ell(\langle e,i \rangle,s) = \max y \leq \hat{\ell}(e,s) \; [\forall x < y \; ( g_e(x)[s]=f_i(x,s))]. \end{align*} $$

Note that, for correct e, $\lim _{s \to \infty } \hat {\ell }(e,s) = \omega $ . Moreover, for such e, if $\hat {\ell }(e,s)>y$ then $X_{e,s}\cup Y_{e,s}\upharpoonright \varphi ^{{X_{e,s}\cup Y_{e,s}}}_{e,s}(y)$ can be preserved by preserving $A_s\upharpoonright \psi _{e,s}^{A_s}(\varphi ^{{X_{e,s}\cup Y_{e,s}}}_{e,s}(y))$ , and if we change $A\upharpoonright y+1$ at a stage $\geq s$ , then some number below $\varphi ^{{X_{e,s}\cup Y_{e,s}}}_{e,s}(y)$ must enter $X_e$ or $Y_e$ at or after this stage too. Also note that, for infinitary $R_{\langle e, i \rangle }$ , $\lim _{s\to \infty } \ell (\langle e,i \rangle ,s) = \omega $ (hence, by $\ell (\langle e,i \rangle ,s) \leq \hat {\ell }(e,s)$ , $\lim _{s\to \infty } \hat {\ell }(e,s) = \omega $ too). In the proof of Theorem 4.1 we also had that, for finitary $R_{\langle e, i \rangle }$ , $\lim _{s\to \infty } \ell (\langle e,i \rangle ,s) \downarrow < \omega $ . This is not true here anymore, for instance, it could be that $\lim \sup _{s\to \infty } \ell (\langle e,i \rangle ,s)=\omega $ but the use of either $\Phi _e$ or $\Psi _e$ goes to infinity. However this has no impact on the strategies since the length function $\ell $ is used to measure agreement and does not on its own cause us to restrain A.

The priority tree T and the relevant parameters related to T are defined as in the previous proof using the revised definition of the length function $\ell $ . Then $\delta (\langle e,i \rangle )=0$ for all infinitary requirements $R_{\langle e, i \rangle }$ . (Though, in contrast to the previous proof, $\delta $ may not be the true path since, as mentioned, now we may have $\limsup _{s\to \infty } \ell (\langle e,i \rangle ,s) = \omega $ for some finitary requirement $R_{\langle e, i \rangle }$ . But this is not relevant for the proof.) Hence, for any infinitary requirement $R_{\langle e, i \rangle }$ and any node $\beta $ extending $\delta \upharpoonright \langle e, i \rangle +1$ , $\langle e,i \rangle $ is $\beta $ -infinitary.

Now, the basic difference to the previous proof is the following. In the set proof, for given e such that $X_e \cup Y_e =A$ , by putting a new number y into A at a stage at which the current parts of $X_e \cup Y_e$ and A agreed on y, we could force y into $X_e$ or $Y_e$ . Now, assuming that e is correct, putting a new number y into A at a stage $s+1$ such that $\hat {\ell }(e,s)> y$ will only guarantee that $X_e$ or $Y_e$ will change on a number $< \varphi ^{X_{e,s} \cup Y_{e,s}}_e(y)$ . This weaker effect forces us to adapt the strategies $P_{\beta }$ for meeting the noncomputability requirements. As a consequence, we have to relax the rules for moving the markers $g_e$ .

We explain the necessary changes by considering the basic module of a strategy $P_{\beta }$ where there is a single $\beta $ -infinitary requirement $R_{\langle e,i \rangle }$ (and where we assume that $\beta \upharpoonright \langle e,i \rangle +1$ is an initial segment of $\delta $ ). There, at some stage $s+1$ , we started the attack by picking $z=s+1$ as tracker, and by letting $y = g_e(z)[s+1]=s+1$ and $x=s+2$ be the first instances of the corresponding agitator and follower, respectively. For the argument, it was crucial, that putting the agitator y into A at a later stage $s'+1$ made $X_e \upharpoonright g_e(z)[s']+1$ or $Y_e \upharpoonright x+1$ change at a stage $s"+1 \geq s'+1$ (since y enters one of these sets at this stage and $y=g_e(z)[s+1] \leq \min \{g_e[z](s'), x\}$ ). The former case gave us the permission to raise the value of the marker $g_e(z)$ (in accordance with the marker rule $(g_1)$ ) at stage $s"+1$ , i.e., let $g_e(z)[s"+1]=s"+1$ . In this case we defined new instances of the agitator and follower, namely we let $y = s"+1$ and $x= s"+2$ , and we iterated the attack with this new parameters (and we argued that this case may happen only finitely often whence eventually the second case must apply unless the requirement $P_{|\beta |}$ is met for some trivial reasons). In the latter case, $Y_e$ permitted the enumeration of x into C at stage $s"+1$ and let us successfully complete the attack at this stage.

In the current setting, putting y into A gives this desired effect only if $\varphi ^{X_{e,s'} \cup Y_{e,s'}}_e(y) \leq g_e(z)[s'] \leq x$ . In order to achieve this, we do the following: having picked the agitator y (at stage y), we wait for the first greater stage $t+1$ such that $\hat {\ell }(e,t)> y$ (whence $\varphi ^{X_{e,t} \cup Y_{e,t}}_e(y) < t$ ), move the marker $g_e(z)$ to the new position $g_e(z)[t+1]=t+1$ at stage $t+1$ , (temporarily) preserve the computation $\Phi ^{X_{e,t} \cup Y_{e,t}}_e(y)$ (by preserving $A \upharpoonright t$ up to the stage at which we put the agitator into A), and pick the follower $x=t+2$ at the next stage. Preserving $A\upharpoonright t$ will help to main the length function; as mentioned before even if the length function becomes unbounded, it does not prevent lower priority strategies from enumerating into A above t.

Moreover, if the agitator y becomes replaced by a new instance $y'$ (at a later stage $y'$ ), we act correspondingly, i.e., at the first greater stage $t'+1$ such that $\hat {\ell }(e,t')> y'$ we move the marker $g_e(z)$ and appoint the new instance $x'=t'+2$ of the follower at the next stage.

Of course, these moves of $g_e(z)$ are not compatible with the marker rule $(g_1)$ , i.e., these moves are not directly permitted by $X_e$ . For correct e, however, these moves are recognizable by $X_e$ via delayed permitting. To be more precise, assume that e is correct. Then $\hat {\ell }(e,s)$ is unbounded in s, whence the function $t(y)= \mu t \geq y (\hat {\ell }(e)[t]> y)$ is total and computable. We claim that $X_e$ can tell whether a position $g_e(z)[s]$ of the marker is final or not. (Note that this is sufficient to compute (the final position of the marker) $g_e(z)$ relative to $X_e$ , since the other marker rules are not affected by these modifications whence, in particular, the marker $g_e(z)$ reaches a final position.) First note that the marker $g_e(z)$ is moved only if z becomes appointed as a tracker (related to e) at stage z, and if $g_e(z)$ is moved at stage $s'+1$ then z is tracker at stage $s'$ and there is a corresponding agitator $y[s']$ at stage $s'$ (appointed at stage $y[s'] \leq s'$ ). So, in order to tell whether $g_e(z)[s]=g_e(z)$ or not, w.l.o.g. we may assume that $z \leq s$ and that z is a tracker at stage s, and we may fix the corresponding agitator $y=y[s]$ at stage s (appointed at stage y). Now distinguish the following two cases. First assume that $s \leq t(y)$ . Then, unless z becomes cancelled earlier, $g_e(z)$ is moved at stage $t(y)+1$ . So, in this case, $g_e(z)[s]=g_e(z)$ iff $g_e(z)[s]=g_e(z)[t(y)+1]$ . Finally, assume that $t(y) < s$ . Then $g_e(z)$ is moved after stage s only if the agitator y is replaced later, where the first replacement must occur at a stage $s'+1$ such that $X_e$ changes on a number $\leq g_e(z)[s]$ at stage $s'$ . So fix $s'$ minimal such that $X_{e,s'} \upharpoonright g_e(z)[s]+1 = X_{e} \upharpoonright g_e(z)[s]+1$ . Now, if $y[s'+1]$ is not defined or $y[s'+1]=y$ then $g_e(z)$ cannot move after stage $s'+1$ whence $g_e(z)[s]=g_e(z)$ iff $g_e(z)[s]=g_e(z)[s'+1]$ . Otherwise, as in the first case, the first move of $g_e(z)$ after stage s (if any) must occur by stage $t(y[s'+1])+1$ whence $g_e(z)[s]=g_e(z)$ iff $g_e(z)[s]=g_e(z)[t(y[s'+1])+1]$ .

Formally, the construction has to be modified as follows. Clause $(1)_m$ has to be split into the following two clauses where waiting for m-lifting ( $m < m^{\beta }$ ) is a new state in which the attack waits to become able to move $g_{e^{\beta }_m}(z^{\beta }_m)$ above the current value of $\varphi ^{X_{e^{\beta }_m} \cup Y_{e^{\beta }_m}}_{e^{\beta }_m}(y^{\beta }_m)$ and to preserve this configuration.

1. (1)_m $P_{\beta }$ waits for an m-tracker at the end of stage s.

   Action. Appoint $z^{\beta }_m[s+1] = s+1$ as m-tracker of $\beta $ and appoint $y^{\beta }_m[s+1] = s+1$ as m-agitator of $\beta $ at stage $s+1$ . Declare that $P_{\beta }$ waits for m-lifting.

2. (1)_m ^′ $P_{\beta }$ waits for m-lifting and $\hat {\ell }(e^{\beta }_m,s)> y^{\beta }_m[s+1]$ .

   Action. Let $g_{e^{\beta }_m}(z^{\beta }_m[s+1])[s+1] = s+1$ . If $m < m^{\beta }-1$ declare that $P_{\beta }$ waits for an $(m+1)$ -tracker. Otherwise declare that $P_{\beta }$ waits for a follower.

Finally, clauses $(5)^Y_m$ and $(5)^X_m$ have to be adjusted as follows where the action corresponding to clause $(5)^Y_m$ is unchanged.

1. (5)_m ^Y $P_{\beta }$ waits for m-permission at the end of stage s and $Y_{e^{\beta }_m,s} \upharpoonright g_{e^{\beta }_m}(z^{\beta }_m[s])[s] +1 \not = Y_{e^{\beta }_m,s-1} \upharpoonright g_{e^{\beta }_m}(z^{\beta }_m[s])[s] +1$ .

2. (5)_m ^X $P_{\beta }$ waits for m-permission at the end of stage s and $X_{e^{\beta }_m,s} \upharpoonright g_{e^{\beta }_m}(z^{\beta }_m[s])[s] +1 \not = X_{e^{\beta }_m,s-1} \upharpoonright g_{e^{\beta }_m}(z^{\beta }_m[s])[s] +1$ .

   Action. Replace the m-agitator $y^{\beta }_m[s]$ by $y^{\beta }_m[s+1]=s+1$ , cancel the follower $x_{\beta }[s]$ , and—if $m < m^{\beta }-1$ —cancel the $m'$ -tracker $z^{\beta }_{m'}[s]$ and the $m'$ -agitator $y^{\beta }_{m'}[s]$ for all $m'$ with $m < m' < m^{\beta }$ . Finally, declare that $P_{\beta }$ waits for m-lifting.

The formal proof of correctness is left to the reader.