Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-28T19:11:58.667Z Has data issue: false hasContentIssue false
  • English
  • Français

NUMBER SYSTEMS WITH SIMPLICITY HIERARCHIES: A GENERALIZATION OF CONWAY’S THEORY OF SURREAL NUMBERS II

Published online by Cambridge University Press:  05 February 2018

PHILIP EHRLICH  and
ELLIOT KAPLAN
PHILIP EHRLICH
Affiliation:
DEPARTMENT OF PHILOSOPHY OHIO UNIVERSITY ATHENS, OH 45701, USAE-mail:ehrlich@ohio.edu
ELLIOT KAPLAN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN URBANA, IL 61801, USAE-mail:eakapla2@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In [16], the algebraico-tree-theoretic simplicity hierarchical structure of J. H. Conway’s ordered field 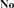${\bf{No}}$ of surreal numbers was brought to the fore and employed to provide necessary and sufficient conditions for an ordered field to be isomorphic to an initial subfield of 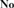${\bf{No}}$, i.e., a subfield of 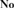${\bf{No}}$ that is an initial subtree of ${\bf{No}}$. In this sequel to [16], analogous results for ordered abelian groups and ordered domains are established which in turn are employed to characterize the convex subgroups and convex subdomains of initial subfields of 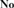${\bf{No}}$ that are themselves initial. It is further shown that an initial subdomain of 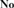${\bf{No}}$ is discrete if and only if it is a subdomain of 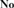${\bf{No}}$’s canonical integer part 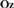${\bf{Oz}}$ of omnific integers. Finally, making use of class models the results of [16] are extended by showing that the theories of nontrivial divisible ordered abelian groups and real-closed ordered fields are the sole theories of nontrivial densely ordered abelian groups and ordered fields all of whose models are isomorphic to initial subgroups and initial subfields of 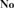${\bf{No}}$.

Keywords

Primary 06A0503C64Secondary 12J1506F2006F25surreal numbersordered abelian groupsordered domainsordered fields
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 617 - 633
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aschenbrenner, M., van den Dries, L., and van der Hoeven, J., The surreal numbers as a universal H-field. Journal of the European Mathematical Society, forthcoming.Google Scholar
Alling, N., Foundations of Analysis Over Surreal Number Fields, North-Holland, Amsterdam, 1987.Google Scholar
Alling, N. and Ehrlich, P., Sections 4.02 and 4.03 of [2].Google Scholar
Alling, N. and Ehrlich, P., An Alternative Construction of Conway’s Surreal Numbers, Comptes rendus mathématiques – Mathematical Reports. Academy of Science, Canada, vol. 8 (1986), pp. 241–246.Google Scholar
Alling, N. and Kuhlmann, S., On ${\eta _\alpha }$-groups and fields. Order, vol. 11 (1994), pp. 85–92.CrossRefGoogle Scholar
Berarducci, A. and Mantova, V., Surreal numbers, derivations and transseries. Journal of the European Mathematical Society, forthcoming.Google Scholar
Boughattas, S., Résultats optimaux sur l’existence d’une partie entière dans les corps ordonnés, this Journal, vol. 58 (1993), pp. 326–333.Google Scholar
Cherlin, G. and Dickmann, M., Real Closed Rings II. Model Theory. Annals of Pure and Applied Logic, vol. 25 (1983), pp. 213–231.CrossRefGoogle Scholar
Chang, C. C. and Keisler, H. J., Model Theory, third ed., North-Holland, Amsterdam, New York, 1990; reprinted Dover Publications, Inc., Mineola, New York, 2012.Google Scholar
Conway, J. H., On Numbers and Games, Academic Press, London, 1976; Second Edition, A K Peters, Ltd., Natick, MA, 2001.Google Scholar
van den Dries, L. and Ehrlich, P., Fields of Surreal Numbers and Exponentiation. Fundamenta Mathematicae, vol. 167 (2001), pp. 173–188; erratum, ibid. 168(2001), pp. 295–297.CrossRefGoogle Scholar
Ehrlich, P., An Alternative Construction of Conway’s Ordered Field No. Algebra Universalis, vol. 25 (1988), pp. 7–16; errata, ibid. 25(1988), p. 233.CrossRefGoogle Scholar
Ehrlich, P., Absolutely Saturated Models, Fundamenta Mathematicae, vol. 133 (1989), pp. 39–46.CrossRefGoogle Scholar
Ehrlich, P., Universally Extending Arithmetic Continua,Le Labyrinthe du Continu, Colloque de Cerisy (Sinaceur, H. and Salanskis, J.-M., editors), Springer-Verlag, France, Paris, 1992, pp. 168–177.Google Scholar
Ehrlich, P., All Number Great and Small, Real Numbers, Generalizations of the Reals, and Theories of Continua (Ehrlich, P., editor), Kluwer Academic Publishers, Dordrecht, Netherlands, 1994, pp. 239–258.CrossRefGoogle Scholar
Ehrlich, P., Number Systems with Simplicity Hierarchies: A Generalization of Conway’s Theory of Surreal Numbers, this Journal, vol. 66 (2001), pp. 1231–1258.Google Scholar
Ehrlich, P., Surreal Numbers: An Alternative Construction (Abstract). Bulletin of Symbolic Logic, vol. 8 (2002), p. 448.Google Scholar
Ehrlich, P., Corrigendum to “Number Systems with Simplicity Hierarchies: A Generalization of Conway’s Theory of Surreal Numbers”, this Journal, vol. 70 (2005), p. 1022.Google Scholar
Ehrlich, P., Conway Names, the Simplicity Hierarchy and the Surreal Number Tree. Journal of Logic and Analysis, vol. 3 (2011), no. 1, pp. 1–26.Google Scholar
Ehrlich, P., The absolute arithmetic continuum and the unification of all numbers great and small. Bulletin of Symbolic Logic, vol. 18 (2012), pp. 1–45.CrossRefGoogle Scholar
Gonshor, H., An Introduction to the Theory of Surreal Numbers, Cambridge University Press, Cambridge, 1986.CrossRefGoogle Scholar
Hahn, H., Über die nichtarchimedischen Grössensysteme, Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, Wien, Mathematisch-Naturwissenschaftliche Klasse 116 (Abteilung IIa), 1907, pp. 601–655.Google Scholar
Kuhlmann, S. and Matusinski, M.. The Exponential-Logarithmic Equivalence Classes of Surreal Numbers. Order, vol. 32 (2015), pp. 53–68.CrossRefGoogle Scholar
Mendelson, E., An Introduction to Mathematical Logic, fifth ed., CRC Press, Boca Raton, 2010.Google Scholar
Schleicher, D. and Stoll, M., An introduction to Conway’s games and numbers. Moscow Mathematical Journal, vol. 6 (2006), pp. 359–358.Google Scholar