Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-11T03:42:08.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Number systems with simplicity hierarchies: a generalization of Conway's theory of surreal numbers

Published online by Cambridge University Press:  12 March 2014

Philip Ehrlich
Philip Ehrlich*
Affiliation:
Department of Philosophy, Ohio University, Athens, OH 45701, USA, E-mail: ehrlich@ohiou.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Introduction. In his monograph On Numbers and Games [7], J. H. Conway introduced a real-closed field containing the reals and the ordinals as well as a great many other numbers including ω, ω, /2, 1/ω, 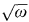and ω − π to name only a few. Indeed, this particular real-closed field, which Conway calls No, is so remarkably inclusive that, subject to the proviso that numbers—construed here as members of ordered “number” fields—be individually definable in terms of sets of von Neumann-Bernays-Gödel set theory with Global Choice, henceforth NBG [cf. 21, Ch. 4], it may be said to contain “All Numbers Great and Small.” In this respect, No bears much the same relation to ordered fields that the system of real numbers bears to Archimedean ordered fields. This can be made precise by saying that whereas the ordered field of reals is (up to isomorphism) the unique homogeneous universal Archimedean ordered field, No is (up to isomorphism) the unique homogeneous universal orderedfield [14]; also see [10], [12], [13].

However, in addition to its distinguished structure as an ordered field, No has a rich hierarchical structure that (implicitly) emerges from the recursive clauses in terms of which it is defined. This algebraico-tree-theoretic structure, or simplicity hierarchy, as we have called it [15], depends upon No's (implicit) structure as a lexicographically ordered binary tree and arises from the fact that the sums and products of any two members of the tree are the simplest possible elements of the tree consistent with No's structure as an ordered group and an ordered field, respectively, it being understood that x is simpler than y just in case x is a predecessor of y in the tree.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 3 , September 2001 , pp. 1231 - 1258
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Alling, N., On the existence of real closed fields that are ηα-sets of power ℵα, Transactions of the American Mathematical Society, vol. 103 (1962), pp. 341–352.Google Scholar
[2]Alling, N., Conway's field of surreal numbers, Transactions of the American Mathematical Society, vol. 287 (1985), pp. 365–386.Google Scholar
[3]Alling, N., Foundations of analysis over surreal number fields, North-Holland Publishing Co., Amsterdam, 1987.Google Scholar
[4]Alling, N. and Ehrlich, P., An alternative construction of Conway's surreal numbers, La Société royale du Canada. Comptes Rendus Mathématiques de l'Académie des Sciences. (Mathematical Reports) VIII, vol. 8 (1986), no. 4, pp. 241–246.Google Scholar
[5]Alling, N. and Ehrlich, P., An abstract characterization of a full class of surreal numbers, La Société royale du Canada. Comptes Rendus Mathématiques de l'Académie des Sciences (Mathematical Reports) VIII, (1986), pp. 303–308.Google Scholar
[6]Alling, N. and Ehrlich, P., Foundations of analysis over surreal number fields, North-Holland Publishing Co., Amsterdam, 1987, Sections 4.02 and 4.03.Google Scholar
[7]Conway, J. H., On numbers and games, Academic Press, 1976.Google Scholar
[8]Dales, H. G. and Woodin, W. H., Super-real ordered fields, Clarendon Press, Oxford, 1996.CrossRefGoogle Scholar
[9]Drake, F., Set theory; an introduction to large cardinals, North-Holland Publishing Co., Amsterdam, 1974.Google Scholar
[10]Ehrlich, P., The absolute arithmetic and geometric continua, PSA 1986 (Lansing, MI) (Arthur Fine and Peter Machamer, editors), vol. 2, Philosophy of Science Association, 1987, pp. 237–247.Google Scholar
[11]Ehrlich, P., An alternative construction of Conway's ordered field No, Algebra Universalis, vol. 25 (1988), pp. 7–16, errata, Algebra Universalis, vol. 25, (1988), page 233.CrossRefGoogle Scholar
[12]Ehrlich, P., Absolutely saturated models, Fundamenta Mathematicae, vol. 133 (1989), pp. 39–46.CrossRefGoogle Scholar
[13]Ehrlich, P., Universally extending continua, Abstracts of papers presented vol. 10, p. 15, American Mathematical Society, 01 1989.Google Scholar
[14]Ehrlich, P., Universally extending arithmetic continua, Le labyrinthe du continu: Colloque de Cerisy (Sinaceur, H. and Salanskis, J. M., editors), Springer-Verlag, Paris, France, 1992, pp. 168–177.Google Scholar
[15]Ehrlich, P., All numbers great and small, Real numbers, generalizations of the reals, and theories of continua, Kluwer Academic Publishers, 1994, pp. 239–258.CrossRefGoogle Scholar
[16]Gaifman, H., Operations on relational structures, functors and classes. I, Proceedings of the Tarski symposium (Henkin, Leonet al., editor), American Mathematical Society, Providence, Rhode Island, 1974, pp. 21–39.Google Scholar
[17]Gonshor, H., An introduction to the theory of surreal numbers, Cambridge University Press, 1986.CrossRefGoogle Scholar
[18]Hahn, H., Über die nichtarchimedischen Grössensysterne, Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, Mathematisch - Naturwissenschaftliche Klasse (Wien), vol. 116, 1907, (Abteilung IIa), pp. 601–655.Google Scholar
[19]Hausner, M. and Wendel, J. G., Ordered vector spaces, Proceedings of the American Mathematical Society, vol. 3, 1952, pp. 977–982.CrossRefGoogle Scholar
[20]Levi, A., Basic set theory, Springer-Verlag, Berlin, 1979.CrossRefGoogle Scholar
[21]Mendelson, E., Introduction to mathematical logic, third ed., Wadsworth & Brooks/Cole Advanced Books & Software, Monterey, California, 1987.CrossRefGoogle Scholar
[22]Mourgues, M. H. and Ressayre, J.-P., A transfinite version of Puiseux's theorem with applications to real closed fields, Logic Colloquium '90, ASL Summer Meetingin Helsinki (Oikkonen, J. and Väänäen, J., editors), Springer-Verlag, Berlin, 1991, pp. 250–258.Google Scholar
[23]Mourgues, M. H. and Ressayre, J.-P., Every real closed field has an integer part, this Journal, vol. 58 (1993), pp. 641–647.Google Scholar
[24]Priess-Crampe, S., Angeordnete Strukturen, Gruppen, Körper, projektive Ebenen, Springer-Verlag, Berlin, 1983.Google Scholar
[25]Rayner, F. J., Algebraically closed fields analogous to fields of Puiseux series, The Journal of the London Mathematical Society, vol. 8 (1974), no. 2, pp. 504–506.CrossRefGoogle Scholar
[26]Sankaran, N. and Venkataraman, R., A generalization of the ordered group of integers, Mathematishe Zeitschrift, vol. 79 (1962), pp. 21–31.CrossRefGoogle Scholar
[27]Sikorski, R., On an ordered algebraic field, Comptes rendus des séances de la classe III, sciences mathématiques et physiques, vol. 41, La Société des Sciences et des Lettres de Varsovie, 1948, pp. 69–96.Google Scholar
[28]Ucsnay, P., Wohlgeordnete Untermengen in totalgeordneten Gruppen mit einer Anwendung auf Potenzreihenkörper, Mathematishe Annalen, vol. 160 (1965), pp. 161–170.CrossRefGoogle Scholar