Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-11T07:49:33.907Z Has data issue: false hasContentIssue false
  • English
  • Français

On Π 1-automorphisms of recursive linear orders

Published online by Cambridge University Press:  12 March 2014

Henry A. Kierstead
Henry A. Kierstead*
Affiliation:
Department of Mathematics and Statistics, University of Calgary, Calgary, Alberta T2N 1N4, Canada Department of Mathematics, University of South Carolina, Columbia, South Carolina 29208
Get access Rights & Permissions [Opens in a new window]

Extract

If σ is the order type of a recursive linear order which has a nontrivial automorphism, we let denote the least complexity in the arithmetical hierarchy such that every recursive order of type σ has a nontrivial automorphism of complexity . In Chapter 16 of his book Linear orderings [R], Rosenstein discussed the problem of determining for certain order types σ. For example Rosenstein proved that 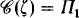, where ζ is the order type of the integers, by constructing a recursive linear order of type ζ which has no nontrivial Σ 1-automorphism and showing that every recursive linear order of type ζ has a nontrivial Π 1-automorphism. Rosenstein also considered linear orders of order type 2 · η, where 2 is the order type of a two-element chain and η is the order type of the rational numbers. It is easily seen that any recursive linear order of type 2 · η has a nontrivial ⊿ 2-automorphism; he showed that there is a recursive linear order of type 2 · η that has no nontrivial Σ 1-automorphism. This left the question, posed in [R] and also by Lerman and Rosenstein in [LR], of whether or ⊿ 2. The main result of this article is that :

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 3 , September 1987 , pp. 681 - 688
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The author was supported in part by NSF grant IPS-80110451, ONR grant N00014-85K-0494, and NSERC grants 69-3378, 69-0259, and 69-1325.

References

REFERENCES

[LR] Lerman, M. and Rosenstein, J., On recursive linear orderinus. II, Patras Logic Symposion (Patras, 1980), North-Holland, Amsterdam, 1981, pp. 123–136.Google Scholar
[R] Rosenstein, J., Linear orderings, Academic Press, New York, 1982.Google Scholar
[S] Schwartz, S., Quotient lattices, index sets, and recursive linear orderings, Ph.D. thesis, University of Chicago, Chicago, Illinois, 1982.Google Scholar