Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T02:04:28.545Z Has data issue: false hasContentIssue false
  • English
  • Français

On an extension of Hilbert's second ε-theorem1

Published online by Cambridge University Press:  12 March 2014

T. B. Flannagan
T. B. Flannagan*
Affiliation:
Bedford College, University of London, London, England
Get access Rights & Permissions [Opens in a new window]

Extract

The aim of this paper is to correct an error in the proof in [2] of a strengthened version of Hilbert's second ε-theorem.

Hilbert's original theorem says (effectively) that formulae of the form ∃xA → A(εxA) can be eliminated from deductions of ∈-free sentences B (i.e. those which do not contain the ε-symbol) from collections X of ε-free sentences. The extended version (Theorem III. 11 of [2]) says that, in addition, instances of Ackermann's schema 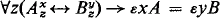can also be eliminated.

The error in [2] occurs in the proof of Theorem III.7 and is described as follows. If A′ is the formula obtained from A by replacing every occurrence of ∃yB by B(εyB) (or ∀yC by C(εyB) if B is of the form ¬ C), and if A is a Q3 or Q4-axiom then, contrary to the claim on p. 73 of [2], A′ is not necessarily an axiom of the same form. For example, if A is the Q3-axiom

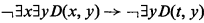
where the rank of εx∃yD(x, y) is ≤ the rank of εyB (see p. 70) and where B is D(t,y), then A′ is

which is not a Q3-axiom. In other words, the notion of rank as defined in [2] is inadequate for the proof of Theorem III.11.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 40 , Issue 3 , September 1975 , pp. 393 - 397
Copyright
Copyright © Association for Symbolic Logic 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The material in this paper is contained in the author's doctoral thesis (Bedford College, London, 1973) which was written under the supervision of Dr. G. T. Kneebone. The author would like to thank the S.R.C. for financial assistance.

References

REFERENCES

[1]Hilbert, D. and Bernays, P., Grundlagen der Mathematik, vol. 2, Berlin, 1939. Reprinted, Ann Arbor, 1944.Google Scholar
[2]Leisenring, A. C., Mathematical logic and Hilbert's ε-symbol, MacDonald, London, 1969.Google Scholar
[3]Leisenring, A. C., Ph.D. Thesis, London, 1967.Google Scholar
[4]Rasiowa, H. and Sikorski, R., The mathematics of metamathematics, 2nd edition, PWN, Warsaw, 1968.Google Scholar