Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Newelski, Ludomir
1998.
M-gap conjecture and m-normal theories.
Israel Journal of Mathematics,
Vol. 106,
Issue. 1,
p.
285.
Tanović, Predrag
2007.
Non-isolated types in stable theories.
Annals of Pure and Applied Logic,
Vol. 145,
Issue. 1,
p.
1.

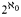 countable models and
countable models and 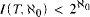 , then we prove that every good
, then we prove that every good 