Article contents
On choice sequences determined by spreads
Published online by Cambridge University Press: 12 March 2014
Extract
From the moment choice sequences appear in Brouwer's writings, they do so as elements of a spread. This led Kreisel to take the so-called axiom of spreaddata as the basic axiom in a formal theory of choice sequences (Kreisel [1965, pp. 133–136]). This axiom expresses the idea that to be given a choice sequence means to be given a spread to which the choice sequence belongs. Subsequently, however, it was discovered that there is a formal clash between this axiom and closure of the domain of choice sequences under arbitrary (lawlike) continuous operations (Troelstra [1968]). For this reason, the formal system CS was introduced (Kreisel and Troelstra [1970]), in which spreaddata is replaced by analytic data. In this system CS, the domain of choice sequences is closed under all continuous operations, and therefore it provides a workable basis for intuitionistic analysis. But the problem whether the axiom of spreaddata is compatible with closure of the domain of choice sequences under the continuous operations from a restricted class, which is still rich enough to validate the typical axioms of continuous choice, remained open. It is precisely this problem that we aim to discuss in this paper.
Recall that a spread is a (lawlike, inhabited) decidable subtree S of the tree N< N of all finite sequences, having all branches infinite:
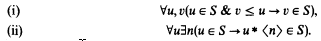
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 3
- Cited by

