Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T03:57:26.656Z Has data issue: false hasContentIssue false
  • English
  • Français

ON CONFIGURATIONS CONCERNING CARDINAL CHARACTERISTICS AT REGULAR CARDINALS

Part of: Set theory

Published online by Cambridge University Press:  10 July 2020

OMER BEN-NERIA  and
SHIMON GARTI
OMER BEN-NERIA
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERUSALEMJERUSALEM91904, ISRAELE-mail: omer.bn@mail.huji.ac.ilE-mail: shimon.garty@mail.huji.ac.il
SHIMON GARTI
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS THE HEBREW UNIVERSITY OF JERUSALEMJERUSALEM91904, ISRAELE-mail: omer.bn@mail.huji.ac.ilE-mail: shimon.garty@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the consistency and consistency strength of various configurations concerning the cardinal characteristics 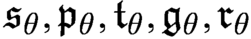$\mathfrak {s}_\theta , \mathfrak {p}_\theta , \mathfrak {t}_\theta , \mathfrak {g}_\theta , \mathfrak {r}_\theta $ at uncountable regular cardinals 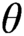$\theta $ . Motivated by a theorem of Raghavan–Shelah who proved that 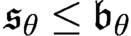$\mathfrak {s}_\theta \leq \mathfrak {b}_\theta $ , we explore in the first part of the paper the consistency of inequalities comparing 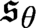$\mathfrak {s}_\theta $ with 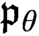$\mathfrak {p}_\theta $ and 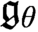$\mathfrak {g}_\theta $ . In the second part of the paper we study variations of the extender-based Radin forcing to establish several consistency results concerning 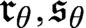$\mathfrak {r}_\theta ,\mathfrak {s}_\theta $ from hyper-measurability assumptions, results which were previously known to be consistent only from supercompactness assumptions. In doing so, we answer questions from [1], [15] and [7], and improve the large cardinal strength assumptions for results from [10] and [3].

Keywords

splitting numberreaping numberpseudointersectiongroupwise densitysupercompact cardinalsconsistency strengthextender-based Radin forcing

MSC classification

Primary: 03E17: Cardinal characteristics of the continuum
Secondary: 03E50: Continuum hypothesis and Martin's axiom 03E55: Large cardinals
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 2 , June 2020 , pp. 691 - 708
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ben-Neria, O. and Gitik, M., On the splitting number at regular cardinals , this Journal, vol. 80 (2015), no. 4, pp. 1348–1360.Google Scholar
Blass, A., Combinatorial cardinal characteristics of the continuum , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), vol. 1, Springer, Dordrecht, 2010, pp. 395–489.CrossRefGoogle Scholar
Brooke-Taylor, A. D., Fischer, V., Friedman, S. D., and Montoya, D. C., Cardinal characteristics at $\;\kappa\;$ in a small $\;u\left(\kappa \right)$ model . Annals of Pure and Applied Logic, vol. 168 (2017), no. 1, pp. 37–49.CrossRefGoogle Scholar
Cummings, J., and Shelah, S., Cardinal invariants above the continuum . Annals of Pure and Applied Logic, vol. 75 (1995), no. 3, pp. 251–268.CrossRefGoogle Scholar
Garti, S., Gitik, M., and Shelah, S., Cardinal characteristics at ${\aleph}_{\omega }$ , Acta Math. Hungarica , vol. 160 (2020), no. 2, pp. 320–336.CrossRefGoogle Scholar
Garti, S. and Shelah, S., Partition calculus and cardinal invariants . Journal of the Mathematical Society of Japan, vol. 66 (2014), no. 2, pp. 425–434.CrossRefGoogle Scholar
Garti, S. and Shelah, S., Open and solved problems concerning polarized partition relations . Fundamenta Mathematicae, vol. 234 (2016), no. 1, pp. 1–14.CrossRefGoogle Scholar
Gitik, M., The negation of the singular cardinal hypothesis from o(K)=K++ , this Journal, vol. 43 (1989), no. 3, pp. 209–234.Google Scholar
Gitik, M., Prikry-type forcings , Handbook of Set Theory, (Foreman, M. and Kanamori, A., editors), vol. 1, Springer, Dordrecht, 2010, pp. 1351–1447.CrossRefGoogle Scholar
Gitik, M. and Shelah, S., On densities of box products . Topology and its Applications, vol. 88 (1998), no. 3, pp. 219–237.CrossRefGoogle Scholar
Kamo, S., Splitting numbers on uncountable regular cardinals, unpublished.Google Scholar
Merimovich, C., Extender-based Magidor-Radin forcing . Israel Journal of Mathematics, vol. 182 (2011), pp. 439–480.CrossRefGoogle Scholar
Radin, L. B., Adding closed cofinal sequences to large cardinals . Annals of Mathematical Logic, vol. 22 (1982), no. 3, pp. 243–261.CrossRefGoogle Scholar
Raghavan, D. and Shelah, S., Two inequalities between cardinal invariants . Fundamenta Mathematicae, vol. 237 (2017), no. 2, pp. 187–200.CrossRefGoogle Scholar
Raghavan, D. and Shelah, S., A small ultrafilter number at smaller cardinals. Archive for Mathematical Logic , vol. 59 (2020), no. 3–4, pp. 325–334.CrossRefGoogle Scholar
Shelah, S. and Spasojević, Z., Cardinal invariants bk and tk . Publications de l’Institut Mathématique, vol. 72 (2002), no. 86, pp. 1–9.CrossRefGoogle Scholar
Suzuki, T., On splitting numbers . Urikaisekikenky usho Koky uroku (1993), no. 818, pp. 118–120, Mathematical logic and applications ’92 (Japanese) (Kyoto, 1992).Google Scholar