Article contents
On confirmation
Published online by Cambridge University Press: 12 March 2014
Extract
Taking for the relation of confirmation the following obvious axioms, we obtain several more or less well-known theorems and are able to solve in a definite and strict manner several problems concerning confirmation.
Let a, b, and c be variable names of sentences belonging to a certain class, the operations a·b, a + b, and ā the (syntactical) product, the sum, and the negation of them. Let us further assume the existence of a real non-negative function c(a, b) of a and b, when b is not self-contradictory. Let us read ‘c(a, b)’ ‘degree of confirmation of a with respect to b' and take the following axioms:
Axiom I. If a is a consequence of b, c(a, b) = 1.
Axiom II. If 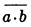 is a consequence of c,
is a consequence of c,
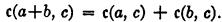
Axiom III. c(a·b, c) = c(a, c)·c(b, a·c).
Axiom IV. If b is equivalent to c, c(a, b) = c(a, c).
As may be easily seen, the interval of variation for c is (0, 1); this is quite conventional.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1940
References
1 The class must be broad enough to include all sentences for which we desire to speak about confirmation.
2 These axioms are analogous to St. Mazurkiewicz's system of axioms for probabilities (see Zur Axiomatik der Wahrscheinlichkeitsrechnung, Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie, vol. 25 (1932))Google Scholar.
3 This fact may be expressed more simply and intuitively as follows. We find in chapters on induction and probability the statement that a hypothesis is the more probable the more facts we have observed following from it. This statement is a special case of f4) if we take the degree of confirmation instead of probability. For, the product of facts a 1.a 2 … a n has a smaller ϲ than the product a 1.a 2 … a n−1—a result easily obtained on the basis of our axioms, provided that an does not follow from a 1.a 2 … a n−1. (If an, does follow, we would not say that we have observed more facts, when an is observed after a 1.a 2 … a n−1.)
Moreover, assuming that we obtain more or stronger knowledge or data by observing or stating facts which were more difficult to anticipate, i.e. less confirmed a priori, we may simply define “more or stronger observed facts or data” by “less confirmed a priori.” Let us therefore say that: F1 are more or stronger observed facts or data than F2 = ϲ(F1, c) < ϲ(F2, c), where c is the knowledge available at the time. This definition allows us to compare—with respect to more or stronger facts or data—not only two sets of facts where the first includes or implies the other, but also two quite independent sets of facts. E.g. an observation of the weather during a whole week constitutes, ceteris paribus, more or stronger facts or data according to our definition than an observation of the weather during one day of another week.
According to this definition, however, f4) becomes equivalent to the simpler and more intuitive statement given at the beginning of this note (in italics). We have only to substitute in it “confirmed” instead of “probable.”
4 We may also say, however, that the distance from 1, when the ϲ of a hypothesis decreases under the influence of a fact, proceeds like an avalanche. If a fact is unfavorable for two hypotheses and its ϲ is equal with respect to both, then the difference in the distance from 1 of the ϲ will be greater for that one of the two hypotheses whose a priori ϲ is greater. This may be easily seen when applying (I′), see p. 144.
5 If a does not follow from b.c, then
as we see from (I′), p. 144. Thus taking ϲ(b, a.c 1.c) instead of ϲ(b, c 1.c) is the less dangerous, the nearer the right hand side of the equality is to 1. If it is equal to 1, we say that b is independent of a, given c 1.c. In that case we can obviously take c(b, a.c 1.c) instead of ϲ(b, c 1.c), since they are equal.
6 This emphasizes the fact that what may increase the c of the instance of the law Every A is B is not the logical product X is A and X is B, but only its second factor (X is B) when the first (X is A) was observed, i.e. when X is A belongs to the knowledge we possess at the given time. For it is X is B which follows from Every A is B and X is A and not X is A from Every A is B. Thus, when I shall speak about the increase of the ϲ of a sentence on the basis of its instance, I shall mean the second factor of the instance, when the first was observed, i.e. when the first belongs to our knowledge already possessed.
7 As a matter of fact the difference between the extensions of the class of substances insoluble in water and of the class of salts alone makes it equal or greater. For the ϲ of the class A being homogeneous with respect to B is equal to or greater than the ϲ of the class ![]() being homogeneous with respect to A—if the extension of
being homogeneous with respect to A—if the extension of ![]() is greater than that of A; and it is greater if ϲ (‘No Ᾱ is
is greater than that of A; and it is greater if ϲ (‘No Ᾱ is ![]() , c) ≠ 0.
, c) ≠ 0.
In fact, ϲ (‘Every or no A is B', c) = ϲ(‘Every A is B', c) + ϲ(‘No A is B', c), ϲ(‘N0 or every ![]() is A', c) = ϲ(‘No
is A', c) = ϲ(‘No![]() is A', ϲ) + ϲ (‘Every A is A', c). The first members of the sums are equal, since ‘Every A is B’ and ‘No
is A', ϲ) + ϲ (‘Every A is A', c). The first members of the sums are equal, since ‘Every A is B’ and ‘No ![]() is A’ are equivalent propositions. (It can be easily shown on the basis of the above axioms that equivalent sentences have the same ϲ.) But ϲ(‘Every
is A’ are equivalent propositions. (It can be easily shown on the basis of the above axioms that equivalent sentences have the same ϲ.) But ϲ(‘Every ![]() is A’, c) = 0, because there are more
is A’, c) = 0, because there are more ![]() 's than A's.
's than A's.
But the difference between the ϲ's of the two homogeneous classes (that of the class A with respect to B and that of the class ![]() with respect to A) may be great or small independently of the difference between the extensions of
with respect to A) may be great or small independently of the difference between the extensions of ![]() and A, unless this last difference is 0.
and A, unless this last difference is 0.
8 At present the c of the generalization ‘Every kitchen salt is soluble in water’ is so high that not only an instance of its contrapositive but also an instance of itself raises its ϲ by a minute value only, because the ϲ of this instance is nearly 1. (See f4), but also f4), p. 134). Moreover, the ϲ of the contrary proposition ‘No kitchen salt is soluble in water’ is at the present state of knowledge near 0, so that the difference between the two homogeneities considered in (ii) is small (see footnote 7). We understand by ‘no kitchen salt’ ‘no kitchen salt not yet examined,’ for otherwise the ϲ of the sentence ‘no kitchen salt is soluble in water’ would be 0.
Instead of the solubility of salt in water, which we took because (kitchen) salt and water are generally known substances, we could consider, e.g., the solubility of boron chloride in diethylene glycol, which is probably not yet examined.
9 The first ϲ being always greater than the second, when NC(![]() ) > NC(A), as the previous demonstration showed.
) > NC(A), as the previous demonstration showed.
10 To make the notion of ‘homogeneity’ clearer let us give the two following examples, the first where the ϲ of the homogeneity is 1 or nearly 1, the second where it is near 0. Let us place one ball in each of a great number of empty urns, putting in a white or a black one according to the outcome of tossing a coin.
1. We make several drawings from one and the same urn, replacing the ball into the urn after each drawing.
2. We make several drawings, each time from a different urn.
Consider the c of the sentence b 2: ‘Every drawing gives a white ball.’ In the first case supposed, one drawing determines the contents of the urn, i.e. makes the ϲ of b 2 equal 1, independently of the extension of its subject term.
11 As a matter of fact the great majority of general sentences which we may think of at random are such that their subject term is less extensive than the negation of their predicate term. And it is so, because, in most cases, the negations of names which are in use are more extensive than the names themselves. Thus, if we think of a general sentence ‘Every A is B’ at random, without artificially constructing it, there is a large chance that ![]() will be more extensive than B and a fortiori than A.
will be more extensive than B and a fortiori than A.
12 In an “existential” sense of the proposition ‘Every A is B,’ this proposition presupposes the existence of A. Thus ‘Every A is B’ is not equivalent to ‘Every B is A’ which presupposes in its turn the existence of ![]() , but does not presuppose the existence of A.
, but does not presuppose the existence of A.
But the paradox persists when we interpret the proposition ‘Every A is B’ and its contrapositive in a nonexistential sense. Furthermore, we have assumed the existence of A (and of ![]() ) in our examples prior to the confirmation of the general proposition. Thus, the rôlle of a confirming instance is not to establish the existence of A.
) in our examples prior to the confirmation of the general proposition. Thus, the rôlle of a confirming instance is not to establish the existence of A.
13 There are hypotheses for which it is expressly assumed that they do not imply any observed fact or for which it can be logically demonstrated that no observable fact could confirm or disconfirm them. But these hypotheses do not exhaust those which are called metaphysical.
14 Instead of (5) the following condition is also sufficient for (4) when (1)–(3) are assumed:
The demonstration is based upon the two equalities,
which are cases of (II).
A necessary and sufficient condition for (4), when (1), (2) and (3′) are assumed, with (3′) as ϲ(a, c) ≠ 1 ϲ(a 2, a 1.c), is:
as is evident from the above two inequalities.
15 There is another demonstration of Theorem 1 by Bernstein, S., Theory of probabilities (in Russian, pp. 84–85)Google Scholar.
16 The dispute is carried on in terms of probability.
17 See Hosiasson, J., Quelques remarques sur la dépendance des probabilités a posteriori de celles a priori, Comptes-rendus du I Congrès des Mathématiciens des Pays Slaves, Warsaw 1930Google Scholar.
18 See footnote 17.
19 Note that we did not here assume condition (8) as to the constancy of ϲ(a 1, a 1.a 2…a s−1.b i.c).
20 See Hosiasson, J., O prawdopodobieństwie hipotez, Przegląd filozoficzny, vol. 39 (1936)Google Scholar.
21 Thus we may say that the ϲ of the logical sum of hypotheses which are not excluded a priori and which confer on the facts a 1, a 2, …, an not certain before being observed a ϲ equal to 1 in the limit, tends to 1 when the number of ai tends to infinity.
22 Maker, P. T., A proof that pure induction approaches certainty as its limit, Mind, vol. 42 (1933), pp. 208–212CrossRefGoogle Scholar.
23 To show this, Keynes' Principle is not needed. See Poirier, , Remarques sur la probabilité des inductions, Paris 1931, p. 31Google Scholar.
24 Philosophy of science, vol. 3 (1936)Google Scholar.
- 66
- Cited by

