Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T19:34:50.125Z Has data issue: false hasContentIssue false
  • English
  • Français

On generic elementary embeddings

Published online by Cambridge University Press:  12 March 2014

Moti Gitik
Moti Gitik*
Affiliation:
School of Mathematical Sciences, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv 69978, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose that I is a precipitous ideal over a cardinal κ and j is a generic embedding of I. What is the nature of j? If we assume the existence of a supercompact cardinal then, by Foreman, Magidor and Shelah [FMS], it is quite unclear where some of such j's are coming from. On the other hand, if ¬∃κ0(κ) = κ++, then, by Mitchell [Mi], the restriction of j to the core model is its iterated ultrapower by measures of it. A natural question arising here is if each iterated ultrapower of 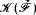can be obtained as the restriction of a generic embedding of a precipitous ideal. Notice that there are obvious limitations. Thus the ultrapower of 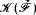by a measure over λ cannot be obtained as a generic embedding by a precipitous ideal over κ ≠ λ. But if we fix κ and use iterated ultrapowers of 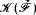which are based on κ, then the answer is positive. Namely a stronger statement is true:

Theorem. Let τ be an ordinal and κ a measurable cardinal. There exists a generic extension V* of V so that NSℵ1 (the nonstationary ideal on ℵ1) is precipitous and, for every iterated ultrapower i of V of length ≤ τ by measures of V based on κ, there exists a stationary set forcing “the generic ultrapower restricted to V is i”.

Our aim will be to prove this theorem. We assume that the reader is familiar with the paper [JMMiP] by Jech, Magidor, Mitchell and Prikry. We shall use the method of that paper for constructing precipitous ideals. Ideas of Levinski [L] for blowing up 2ℵ1 preserving precipitousness and of our own earlier paper [Gi] for linking together indiscernibles will be used also.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 54 , Issue 3 , September 1989 , pp. 700 - 707
Copyright
Copyright © Association for Symbolic Logic 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[CK]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[FMS]Foreman, M., Magidor, M. and Shelah, S., Martin's maximum, saturated ideals, and nonregular ultrafilters, Annals of Mathematics, ser. 2, vol. 127 (1988), pp. 1–47.CrossRefGoogle Scholar
[G]Gaifman, H., Elementary embeddings of models of set-theory and certain subtheories, Axiomatic set theory (Jech, T., editor), Proceedings of Symposia in Pure Mathematics, vol. 13, part 2, American Mathematical Society, Providence, Rhode Island, 1974, pp. 33–101.CrossRefGoogle Scholar
[Gi]Gitik, M., On nonminimal p-points over a measurable cardinal, Annals of Mathematical Logic, vol. 20 (1981), pp. 269–288.CrossRefGoogle Scholar
[JMMiP]Jech, T., Magidor, M., Mitchell, W. and Prikry, K., Precipitous ideals, this Journal, vol. 45 (1980), pp. 1–8.Google Scholar
[K]Kunen, K., Some applications of iterated ultrapowers in set theory, Annals of Mathematical Logic, vol. 1 (1970), pp. 179–227.CrossRefGoogle Scholar
[L]Levinski, J.-P., Thèse du Troisième Cycle, Université Paris-VII, Paris, 1980.Google Scholar
[Mi]Mitchell, W., The core model for sequences of measures. I, Mathematical Proceedings of the Cambridge Philosophical Society, vol. 95 (1984), pp. 229–260.CrossRefGoogle Scholar