Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ikeda, Koichiro
and
Kikyo, Hirotaka
2012.
On superstable generic structures.
Archive for Mathematical Logic,
Vol. 51,
Issue. 5-6,
p.
591.
Gunatilleka, Danul K.
2021.
The theories of Baldwin–Shi hypergraphs and their atomic models.
Archive for Mathematical Logic,
Vol. 60,
Issue. 7-8,
p.
879.

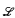 be a finite relational language and
be a finite relational language and