Hostname: page-component-7b9c58cd5d-hpxsc Total loading time: 0 Render date: 2025-03-15T00:31:41.042Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GROUPS WITH DEFINABLE F-GENERICS DEFINABLE IN P-ADICALLY CLOSED FIELDS

Part of: General

Published online by Cambridge University Press:  09 June 2023

ANAND PILLAY  and
NINGYUAN YAO Open the ORCID record for NINGYUAN YAO [Opens in a new window]
ANAND PILLAY
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME NOTRE DAME, IN 46556, USA E-mail: anand.pillay.3@nd.edu
NINGYUAN YAO*
Affiliation:
SCHOOLE OF PHILOSOPHY FUDAN UNIVERSITY SHANGHAI 200433, CHINA
*
E-mail: yaony88@126.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this paper is to develop the theory of groups definable in the p-adic field 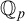${{\mathbb {Q}}_p}$, with “definable f-generics” in the sense of an ambient saturated elementary extension of 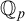${{\mathbb {Q}}_p}$. We call such groups definable f-generic groups.

So, by a “definable f-generic” or 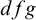$dfg$ group we mean a definable group in a saturated model with a global f-generic type which is definable over a small model. In the present context the group is definable over 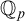${{\mathbb {Q}}_p}$, and the small model will be 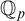${{\mathbb {Q}}_p}$ itself. The notion of a 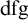$\mathrm {dfg}$ group is dual, or rather opposite to that of an 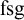$\operatorname {\mathrm {fsg}}$ group (group with “finitely satisfiable generics”) and is a useful tool to describe the analogue of torsion-free o-minimal groups in the p-adic context.

In the current paper our group will be definable over 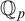${{\mathbb {Q}}_p}$ in an ambient saturated elementary extension 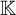$\mathbb {K}$ of 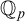${{\mathbb {Q}}_p}$, so as to make sense of the notions of f-generic type, etc. In this paper we will show that every definable f-generic group definable in 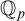${{\mathbb {Q}}_p}$ is virtually isomorphic to a finite index subgroup of a trigonalizable algebraic group over 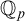${{\mathbb {Q}}_p}$. This is analogous to the o-minimal context, where every connected torsion-free group definable in 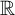$\mathbb {R}$ is isomorphic to a trigonalizable algebraic group [5, Lemma 3.4]. We will also show that every open definable f-generic subgroup of a definable f-generic group has finite index, and every f-generic type of a definable f-generic group is almost periodic, which gives a positive answer to the problem raised in [28] of whether f-generic types coincide with almost periodic types in the p-adic case.

Keywords

p-adically closed fieldsdefinable groupsdefinable f-generic

MSC classification

Primary: 00-01: Instructional exposition (textbooks, tutorial papers, etc.)
Type
Article
Information
The Journal of Symbolic Logic , Volume 88 , Issue 4 , December 2023 , pp. 1334 - 1353
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, J., Minimal Flows and Their Extensions, North Holland, Amsterdam, 1988.Google Scholar
Belair, L., Panorama of p-adic model theory . Annales des Sciences Mathématiques du Québec, vol. 36 (2012), no. 1, pp. 1–33.Google Scholar
Borel, A. and Tits, J., Groupes reductifs . Publications Mathématiques de l’IHÉS, vol. 27 (1965), pp. 55–151.CrossRefGoogle Scholar
Chernikov, A. and Simon, P., Definably amenable $NIP$ groups . Journal of the American Mathematical Society, vol. 31 (2018), pp. 609–641.Google Scholar
Conversano, A., Onshuus, A., and Starchenko, S., Solvable lie groups definable in o-minimal theories . Journal of the Institute of Mathematics of Jussieu, vol. 17 (2018), pp. 441–452.Google Scholar
Conversano, A. and Pillay, A., Connected components of definable groups and $o$ -minimality I . Advances in Mathematics, vol. 231 (2012), pp. 605–623.Google Scholar
Dolich, A., Goodrick, J., and Lippel, D., Dp-minimality: Basic facts and examples . Notre Dame Journal of Formal Logic, vol. 52 (2011), pp. 267–288.Google Scholar
Dries, L. van den, Algebraic theories with definable Skolem functions, Journal of Symbolic Logic, vol. 49 (1984), pp. 625–629.Google Scholar
Dries, L. van den and Scowcroft, P., On the structure of semialgebraic sets over $p$ -adic fields, Journal of Symbolic Logic, vol. 53 (1988), pp. 1138–1164.Google Scholar
Guerrero, P. A. and Johnson, W., Around definable types in $p$ -adically closed fields, preprint, 2022, arXiv:2208.05815v1 [math.LO].Google Scholar
Hrushovski, E., Peterzil, Y., and Pillay, A., Groups, measures, and the $NIP$ . Journal of the American Mathematical Society, vol. 21 (2008), pp. 563–596.Google Scholar
Hrushovski, E. and Pillay, A., Groups definable in local fields and pseudo-finite fields . Israel Journal of Mathematics, vol. 85 (1994), pp. 203–262.Google Scholar
Hrushovski, E. and Pillay, A., On $NIP$ and invariant measures . Journal of the European Mathematical Society, vol. 13 (2011), pp. 1005–1061.Google Scholar
Hrushovski, E., Pillay, A., Simon, P., A note on generically stable measures and fsg groups . Notre Dame Journal of Formal Logic, vol. 53 (2012), pp. 599–605.Google Scholar
Jagiella, G., Definable topological dynamics and real lie groups . Mathematical Logic Quarterly, vol. 61 (2015), nos. 1–2, pp. 45–55.Google Scholar
Johnson, W., A note on $\textit{fsg}$ groups in $p$ -adically closed fields. Mathematical Logic Quarterly, vol. 69 (2023), no. 1, pp. 50–57.Google Scholar
Johnson, W. and Yao, N., On non-compact p-adic definable groups, Journal of Symbolic Logic, vol. 87 (2022), no. 1, pp. 188–213.Google Scholar
Macintyre, A., On definable subsets of p-adic fields, Journal of Symbolic Logic, vol. 41 (1976), pp. 605–610.Google Scholar
Marker, D., Model Theory: An Introduction, Springer-Verlag, New York, 2002.Google Scholar
Milne, J. S., Algebraic Groups, the Theory of Group Schemes of Finite Type over a Field, Cambridge University Press, Cambridge, 2017.Google Scholar
Montenegro, S., Onshuus, A., and Simon, P., Stabilizers, groups with $f$ -generics in ${NTP}_2$ and PRC fields . Journal of the Institute of Mathematics of Jussieu, vol. 19 (2020), pp. 821–853.Google Scholar
Newelski, L., Topological dynamics of definable group actions, Journal of Symbolic Logic, vol. 74 (2009), pp. 50–72.Google Scholar
Onshuus, A. and Pillay, A., Definable groups and compact p-adic lie groups . Journal of the London Mathematical Society, vol. 78 (2008), no. 1, pp. 233–247.Google Scholar
Penazzi, D., Pillay, A., and Yao, N., Some model theory and topological dynamics of p-adic algebraic groups . Fundamenta Mathematicae, vol. 247 (2019), pp. 191–216.Google Scholar
Pillay, A., On fields definable in ${\mathbb{Q}}_p$ . Archive for Mathematical Logic, vol. 29 (1989), pp. 1–7.Google Scholar
Pillay, A., Model theory of algebraically closed fields , Model Theory and Algebraic Geometry (Bouscaren, E., editor), Lecture Notes in Mathematics, vol. 1696, Springer, Berlin, 1998, pp. 61–84.Google Scholar
Pillay, A., Topological dynamics and definable groups, Journal of Symbolic Logic, vol. 78 (2013), pp. 657–666.Google Scholar
Pillay, A. and Yao, N., On minimal flows, definably amenable groups, and o-minimality . Advances in Mathematics, vol. 290 (2016), pp. 483–502.Google Scholar
Pillay, A. and Yao, N., A note on groups definable in the p-adic field . Archive for Mathematical Logic, vol. 58 (2019), pp. 1029–1034.Google Scholar
Platonov, V. and Rapinchuk, A., Algebraic Groups and Number Theory, Academic Press, San Diego, CA, 1994.Google Scholar
Poizat, B., A Course in Model Theory, Spinger-Verlag, New York, 2000.Google Scholar
Serre, J.-P., Lie Groups and Lie Algebras, Benjamin, New York, 1965.Google Scholar
Simon, P., Finding generically stable measures, Journal of Symbolic Logic, vol. 77 (2012), pp. 263–278.Google Scholar
Simon, P., Distal and non-distal $NIP$ theories . Annals of Pure and Applied Logic, vol. 164 (2013), pp. 294–318.Google Scholar
Simon, P., Dp-minimality: Invariant types and dp-rank, Journal of Symbolic Logic, vol. 79 (2014), pp. 1025–1045.Google Scholar
Wang, S. P., On anisotropic solvable linear algebraic groups . Proceedings of the American Mathematical Society, vol. 84 (1982), no. 1, pp. 11–15.Google Scholar
Yao, N., Definable topological dynamics for Trigonalizable algebraic groups over ${\mathbb{Q}}_p$ . Mathematical Logic Quarterly, vol. 65 (2019), no. 3, pp. 376–386.Google Scholar
Yao, N. and Long, D., Topological dynamics for groups definable in real closed field . Annals of Pure and Applied Logic, vol. 166 (2015), pp. 261–273.Google Scholar