No CrossRef data available.
Article contents
On inverse γ-systems and the number of L∞λ-equivalent, non-isomorphic models for λ singular
Published online by Cambridge University Press: 12 March 2014
Abstract
Suppose λ is a singular cardinal of uncountable cofinality κ. For a model 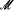 of cardinality λ, let No(
of cardinality λ, let No(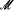 ) denote the number of isomorphism types of models
) denote the number of isomorphism types of models 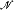 of cardinality λ which are L∞λ-equivalent to
of cardinality λ which are L∞λ-equivalent to 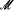 . In [7] Shelah considered inverse κ-systems
. In [7] Shelah considered inverse κ-systems 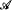 of abelian groups and their certain kind of quotient limits Gr(
of abelian groups and their certain kind of quotient limits Gr(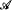 )/ Fact(
)/ Fact(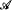 ). In particular Shelah proved in [7, Fact 3.10] that for every cardinal Μ there exists an inverse κ-system
). In particular Shelah proved in [7, Fact 3.10] that for every cardinal Μ there exists an inverse κ-system 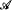 such that
such that 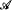 consists of abelian groups having cardinality at most Μκ and card(Gr(
consists of abelian groups having cardinality at most Μκ and card(Gr(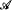 )/ Fact(
)/ Fact(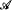 )) = Μ. Later in [8, Theorem 3.3] Shelah showed a strict connection between inverse κ-systems and possible values of No (under the assumption that θκ < λ for every θ < λ): if
)) = Μ. Later in [8, Theorem 3.3] Shelah showed a strict connection between inverse κ-systems and possible values of No (under the assumption that θκ < λ for every θ < λ): if 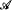 is an inverse κ-system of abelian groups having cardinality < λ, then there is a model
is an inverse κ-system of abelian groups having cardinality < λ, then there is a model 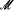 such that card(
such that card(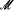 ) = λ and No(
) = λ and No(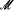 ) = card(Gr(
) = card(Gr(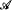 )/ Fact(
)/ Fact(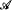 )). The following was an immediate consequence (when θκ < λ for every θ < λ): for every nonzero Μ < λ or Μ = λκ there is a model
)). The following was an immediate consequence (when θκ < λ for every θ < λ): for every nonzero Μ < λ or Μ = λκ there is a model 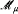 , of cardinality λ with No(
, of cardinality λ with No(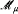 ) = Μ. In this paper we show: for every nonzero Μ ≤ λκ there is an inverse κ-system
) = Μ. In this paper we show: for every nonzero Μ ≤ λκ there is an inverse κ-system 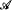 of abelian groups having cardinality < λ such that card(Gr(
of abelian groups having cardinality < λ such that card(Gr(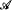 )/ Fact(
)/ Fact(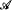 )) = Μ (under the assumptions 2κ < λ and θ<κ < λ for all θ < λ when Μ > λ), with the obvious new consequence concerning the possible value of No. Specifically, the case No(
)) = Μ (under the assumptions 2κ < λ and θ<κ < λ for all θ < λ when Μ > λ), with the obvious new consequence concerning the possible value of No. Specifically, the case No(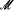 ) = λ is possible when θκ > λ for every λ < λ.
) = λ is possible when θκ > λ for every λ < λ.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000

