Article contents
On large cardinals and partition relations
Published online by Cambridge University Press: 12 March 2014
Extract
A significant portion of the study of large cardinals in set theory centers around the concept of “partition relation”. To best capture the basic idea here, we introduce the following notation: for x and y sets, κ an infinite cardinal, and γ an ordinal less than κ, we let [x]γ denote the collection of subsets of x of order-type γ and abbreviate with 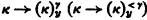 the partition relation for each function F from
the partition relation for each function F from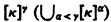 into y there exists a subset C of κ of cardinality κ such that (such that for each α < γ) the range of F on [С]γ ([С]α) has cardinality 1. Now although each infinite cardinal κ satisfies the relation
into y there exists a subset C of κ of cardinality κ such that (such that for each α < γ) the range of F on [С]γ ([С]α) has cardinality 1. Now although each infinite cardinal κ satisfies the relation 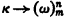 for each n and m in ω (F. P. Ramsey [8]), a connection with large cardinals arises when one asks, “For which uncountable κ do we have κ → (κ)2?” Indeed, any uncountable cardinal κ which satisfies κ → (κ)2 is strongly inaccessible and weakly compact (see [9]). As another example one can look at the improvements of Scott's original result to the effect that if there exists a measurable cardinal then there exists a nonconstructible set. Indeed, if κ is a measurable cardinal then κ → (κ)< ω, and as Solovay [11] has shown, if there exists a cardinal κ such that κ → (κ)< ω3 (κ → (ℵ1)< ω, even) then there exists a nonconstructible
for each n and m in ω (F. P. Ramsey [8]), a connection with large cardinals arises when one asks, “For which uncountable κ do we have κ → (κ)2?” Indeed, any uncountable cardinal κ which satisfies κ → (κ)2 is strongly inaccessible and weakly compact (see [9]). As another example one can look at the improvements of Scott's original result to the effect that if there exists a measurable cardinal then there exists a nonconstructible set. Indeed, if κ is a measurable cardinal then κ → (κ)< ω, and as Solovay [11] has shown, if there exists a cardinal κ such that κ → (κ)< ω3 (κ → (ℵ1)< ω, even) then there exists a nonconstructible  set of integers.
set of integers.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1971
References
- 5
- Cited by

