Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T01:55:43.932Z Has data issue: false hasContentIssue false
  • English
  • Français

ON PRODUCTS OF ELEMENTARILY INDIVISIBLE STRUCTURES

Published online by Cambridge University Press:  12 August 2016

NADAV MEIR
NADAV MEIR*
Affiliation:
DEPARTMENT OF MATHEMATICS BEN-GURION UNIVERSITY OF THE NEGEV P.O.B 653, BE’ER SHEVA 8410501, ISRAELE-mail: mein@math.bgu.ac.ilURL: http://www.math.bgu.ac.il/∼mein
Get access Rights & Permissions [Opens in a new window]

Abstract

We say a structure 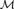${\cal M}$ in a first-order language ${\cal L}$ is indivisible if for every coloring of its universe in two colors, there is a monochromatic substructure 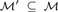${\cal M}\prime \subseteq {\cal M}$ such that 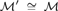${\cal M}\prime \cong {\cal M}$. Additionally, we say that 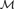${\cal M}$ is symmetrically indivisible if 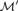${\cal M}\prime$ can be chosen to be symmetrically embedded in 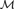${\cal M}$ (that is, every automorphism of 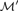${\cal M}\prime$ can be extended to an automorphism of 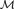${\cal M}$). Similarly, we say that 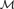${\cal M}$ is elementarily indivisible if 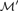${\cal M}\prime$ can be chosen to be an elementary substructure. We define new products of structures in a relational language. We use these products to give recipes for construction of elementarily indivisible structures which are not transitive and elementarily indivisible structures which are not symmetrically indivisible, answering two questions presented by A. Hasson, M. Kojman, and A. Onshuus.

Keywords

03C1003C3505D1005C55indivisibilityelementary indivisibilitycoloringquantifier elimination
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 3 , September 2016 , pp. 951 - 971
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bonato, A., Cameron, P., and Delić, D., Tournaments and orders with the pigeonhole property . Canadian Mathematical Bulletin, vol. 43 (2000), no. 4, pp. 397–405.Google Scholar
Bonato, A. and Delić, D., A pigeonhole property for relational structures . Mathematical Logic Quarterly, vol. 45 (1999), no. 3, pp. 409–413.CrossRefGoogle Scholar
Cherlin, G. L., The classification of countable homogeneous directed graphs and countable homogeneous n-tournaments . Memoirs of the American Mathematical Society, vol. 131 (1998), no. 621.CrossRefGoogle Scholar
Delhommé, C., Laflamme, C., Pouzet, M., and Sauer, N., Divisibility of countable metric spaces . European Journal of Combinatorics, vol. 28 (2007), no. 6, pp. 1746–1769.CrossRefGoogle Scholar
El-Zahar, M. M. and Sauer, N. W., On the divisibility of homogeneous directed graphs . Canadian Journal of Mathematics, vol. 45 (1993), no. 2, pp. 284–294.Google Scholar
El-Zahar, M. M. and Sauer, N. W., On the divisibility of homogeneous hypergraphs . Combinatorica, vol. 14 (1994), no. 2, pp. 159–165.CrossRefGoogle Scholar
Fraïssé, R., Sur l’extension aux relations de quelques propriétés des ordres . Annales Scientifiques de l’École Normale Supérieure (3), vol. 71 (1954), pp. 363–388.Google Scholar
Fraïssé, R., Theory of Relations, revised ed., Studies in Logic and the Foundations of Mathematics, vol. 145, North-Holland, Amsterdam, 2000.Google Scholar
Geschke, S. and Kojman, M., Symmetrized induced Ramsey theory . Graphs and Combinatorics, vol. 27 (2011), no. 6, pp. 851–864.Google Scholar
Hasson, A., Kojman, M., and Onshuus, A., On symmetric indivisibility of countable structures , Model Theoretic Methods in Finite Combinatorics, Contemporary Mathematics, vol. 558, American Mathematical Society, Providence, RI, 2011, pp. 417–452.Google Scholar
Henson, C. W., A family of countable homogeneous graphs . Pacific Journal of Mathematics, vol. 38 (1971), pp. 69–83.Google Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.Google Scholar
Komjáth, P. and Rödl, V., Coloring of universal graphs . Graphs and Combinatorics, vol. 2 (1986), no. 1, pp. 55–60.Google Scholar
Lachlan, A. H., Homogeneous structures , Proceedings of the International Congress of Mathematicians, Vol. 1, 2 (Berkeley, California, 1986), American Mathematical Society, Providence, RI, 1987, pp. 314–321.Google Scholar
Macpherson, H. D., A survey of homogeneous structures . Discrete Mathematics, vol. 311 (2011), no. 15, pp. 1599–1634.CrossRefGoogle Scholar
Marker, D., Model Theory, Graduate Texts in Mathematics, vol. 217, Springer-Verlag, New York, 2002.Google Scholar
Sauer, N. W., Age and weak indivisibility. European Journal of Combinatorics, vol. 37 (2014), pp. 24–31.Google Scholar