Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T18:47:54.307Z Has data issue: false hasContentIssue false
  • English
  • Français

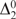ON REALS WITH ${\rm{\Delta }}_2^0$-BOUNDED COMPLEXITY AND COMPRESSIVE POWER

Published online by Cambridge University Press:  14 September 2016

IAN HERBERT
IAN HERBERT*
Affiliation:
DEPARTMENT OF MATHEMATICS NATIONAL UNIVERSITY OF SINGAPORE SINGAPOREE-mail: ian.herbert@csuci.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The (prefix-free) Kolmogorov complexity of a finite binary string is the length of the shortest description of the string. This gives rise to some ‘standard’ lowness notions for reals: A is K-trivial if its initial segments have the lowest possible complexity and A is low for K if using A as an oracle does not decrease the complexity of strings by more than a constant factor. We weaken these notions by requiring the defining inequalities to hold only up to all 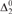${\rm{\Delta }}_2^0$ orders, and call the new notions 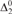${\rm{\Delta }}_2^0$-bounded K-trivial and 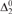${\rm{\Delta }}_2^0$-bounded low for K. Several of the ‘nice’ properties of K-triviality are lost with this weakening. For instance, the new weaker definitions both give uncountable set of reals. In this paper we show that the weaker definitions are no longer equivalent, and that the 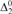${\rm{\Delta }}_2^0$-bounded K-trivials are cofinal in the Turing degrees. We then compare them to other previously studied weakenings, namely infinitely-often K-triviality and weak lowness for K (in each, the defining inequality must hold up to a constant, but only for infinitely many inputs). We show that 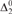${\rm{\Delta }}_2^0$-bounded K-trivial implies infinitely-often K-trivial, but no implication holds between 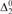${\rm{\Delta }}_2^0$-bounded low for K and weakly low for K.

Keywords

Algorithmic RandomnessKolmogorov complexityK-trivials
Type
Articles
Information
The Journal of Symbolic Logic , Volume 81 , Issue 3 , September 2016 , pp. 833 - 855
Copyright
Copyright © The Association for Symbolic Logic 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baartse, M., and Barmpalias, G., On the gap between trivial and nontrivial initial segment prefix-free complexity . Theory of Computing Systems, vol. 52 (2013), no. 1, pp. 28–47.CrossRefGoogle Scholar
Barmpalias, G., and Lewis, A. E. M., Chaitin’s halting probability and the compression of strings using oracles . Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences, vol. 467 (2011), no. 2134, pp. 2912–2926.Google Scholar
Barmpalias, G., and Vlek, C. S., Kolmogorov complexity of initial segments of sequences and arithmetical definability . Theoretical Computer Science, vol. 412 (2011), no. 41, pp. 5656–5667.CrossRefGoogle Scholar
Chaitin, G. J., Information-theoretic characterizations of recursive infinite strings . Theoretical Computer Science, vol. 2 (1976), no. 1, pp. 45–48.CrossRefGoogle Scholar
Csima, B. F., and Montalbán, A., A minimal pair of K-degrees . Proceedings of the American Mathematical Society, vol. 134 (2006), no. 5, pp. 1499–1502.CrossRefGoogle Scholar
Downey, R. G., Hirschfeldt, D. R., and LaForte, G., Randomness and reducibility . Journal of Computer and System Sciences, vol. 68 (2004), no. 1, pp. 96–114.Google Scholar
Downey, R. G., Hirschfeldt, D. R., Nies, A., and Stephan, F., Trivial Reals, Proceedings of the 7th and 8th Asian Logic Conferences (Singapore, 2003), Singapore University Press, pp. 103–131.Google Scholar
Herbert, I., A perfect set of reals with finite self-information, this Journal, vol. 78 (2013), no. 4, pp.1229–1246.Google Scholar
Hirschfeldt, D. R., and Weber, R., Finite self-information , Computability vol. 1 (2012), no. 1, pp. 85–97.Google Scholar
Miller, J. S., The K-degrees, low for K-degrees, and weakly low for K sets . Notre Dame Journal of Formal Logic, vol. 50 (2009–10), no. 4, pp. 381–391.CrossRefGoogle Scholar
Nies, A., Lowness properties and randomness . Advances in Mathematics, vol. 197 (2005), no. 1, pp. 274–305.Google Scholar
Nies, A., Computability and Randomness, Oxford Logic Guides, vol. 51, Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar
Nies, A., Stephan, F., and Terwijn, S. A., Randomness, relativization and Turing degrees, this Journal, vol. 70 (2005), no. 2, pp. 515–535.Google Scholar
Soare, R. I., Recursively Enumerable Sets and Degrees, Perspectives in Mathematical Logic. Springer-Verlag, Berlin, 1987.Google Scholar
Yu, L., Ding, D., and Downey, R., The Kolmogorov complexity of random reals . Annals of Pure and Applied Logic, vol. 129 (2004), no. 1–3, pp. 163–180.CrossRefGoogle Scholar