Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T20:17:43.753Z Has data issue: false hasContentIssue false
  • English
  • Français

On recursive enumerability with finite repetitions

Published online by Cambridge University Press:  12 March 2014

Stephan Wehner
Stephan Wehner*
Affiliation:
Department of Chemistry, University of British Columbia, Vancouver, British Columbia, V6T 1Z1, Canada E-mail: stephan@pepe.chem.ubc.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

It is an open problem within the study of recursively enumerable classes of recursively enumerable sets to characterize those recursively enumerable classes which can be recursively enumerated without repetitions. This paper is concerned with a weaker property of r.e. classes, namely that of being recursively enumerable with at most finite repetitions.

This property is shown to behave more naturally: First we prove an extension theorem for classes satisfying this property. Then the analogous theorem for the property of recursively enumerable classes of being recursively enumerable with a bounded number of repetitions is shown not to hold. The index set of the property of recursively enumerable classes “having an enumeration with finite repetitions” is shown to be 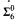-complete.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 64 , Issue 3 , September 1999 , pp. 927 - 945
Copyright
Copyright © Association for Symbolic Logic 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Florence, J. B., Infinite subclasses of recursively enumerable classes, Proceedings of the American Mathematical Society, vol. 15 (1967), pp. 633–639.CrossRefGoogle Scholar
[2] Friedberg, R. M., Three theorems on recursive enumeration: I, Decomposition II, Maximal set III, Enumeration without duplication, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
[3[ Kummer, Martin, Beiträge zur Theorie der Numerierungen: Eindeutige Numerierungen, Dissertation, Universität Karlsruhe, Germany, 1989.Google Scholar
[4] Kummer, Martin, Numberings of R1 ∪ F, Computer Science Logic 1988, Lecture Notes in Computer Science, no. 385, Springer-Verlag, Berlin, 1989, pp. 166–186.Google Scholar
[5] Kummer, Martin, An easy priority-free proof of a theorem of Friedberg, Theoretical Computer Science, vol. 74 (1990), pp. 249–251.CrossRefGoogle Scholar
[6] Lachlan, Alistair, On recursive enumeration without repetition, Zeitschrift für mathematische logik undgrundlagen der mathematik, vol. 11, 1965, pp. 209–220.CrossRefGoogle Scholar
[7] Pour-El, Marian Boykan and Putnam, Hilary, Recursively enumerable classes and their application to recursive sequences of formal theories, Archiv für Mathematische Logik und Grundlagenforschung, vol. 8 (1965), pp. 104–121.CrossRefGoogle Scholar
[8] Wehner, Stephan, The index set of injectively enumerable classes of recursively enumerable sets is σ5 complete, Mathematical Logic Quarterly, vol. 40 (1994), pp. 87–94.Google Scholar
[9] Wehner, Stephan, Computably enumerable classes and the problem of repetitions, Dissertation , Simon Fraser University, Burnaby, Canada, 1995.Google Scholar
[10] Wehner, Stephan, On injective enumerability of recursively enumerable classes of cofinite sets, Archive for Mathematical Logic, vol. 34 (1995), pp. 183–196.CrossRefGoogle Scholar
[11] Young, Paul, A theorem on recursively enumerable classes and splinters, Proceedings of the American Mathematical Society, vol. 17 (1966), pp. 1050–1056.CrossRefGoogle Scholar