Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:15:20.525Z Has data issue: false hasContentIssue false
  • English
  • Français

On reduction to a symmetric relation

Published online by Cambridge University Press:  12 March 2014

William Craig  and
W. V. Quine
William Craig
Affiliation:
Harvard University
W. V. Quine
Affiliation:
Harvard University
Get access Rights & Permissions [Opens in a new window]

Extract

In a current paper, Church and Quine show how any dyadic relation of natural numbers can be defined in terms of a symmetric dyadic relation of natural numbers together with the truth functions and quantification over natural numbers. The purpose of the present note is to extend their result to the following: Where R1, R2, …, ad infinitum are any classes or relations (of any degree) of natural numbers, they can all be defined in terms of a single symmetric dyadic relation of natural numbers together with the truth functions and quantification over natural numbers.

Let pi, for each i, be the tth prime > 1. Let the degree of Ri, for each i, be di. Let R be the dyadic relation which each number x bears to each number y such that either x is a factor of y or else x is 0 and y is 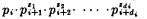for some 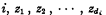such that 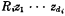. Since R is dyadic, we know from Church and Quine's result that R is definable in terms of a symmetric dyadic relation. Moreover, as seen in the incidental constructions in §1 of Church and Quine, ‘y = x + 1’ is expressible on the same basis.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 17 , Issue 3 , September 1952 , pp. 188
Copyright
Copyright © Association for Symbolic Logic 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Alonzo Church and W. V. Quine, Some theorems on definability and decidability, in this number of this Journal.

2 Robinson, Julia, Definability and decision problems in arithmetic, this Journal, vol. 14 (1949), pp. 98–114Google Scholar.

3 The above theorem continues to hold when we drop the truth functions and quantification and substitute Myhill's version of the ü-operator (a reduction in the number of primitive ideas of arithmetic, this Journal, vol. 15 (1950), p. 130). For, the symmetric dyadic relation of the above proof is specified by Church and Quine's (1)-(10), given R; and from this specification it follows that the relation will serve the purpose of ϕ in Myhill's third paragraph. This point was brought to our attention by Kurt Bing. Incidentally, Church and Quine's Theorem V admits of a similar variant: Elementary number theory can be expressed in terms of just the ü-operator and the symmetric dyadic H which is described in connection with Theorem V. (Added July 15, 1952.)