Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T16:27:24.817Z Has data issue: false hasContentIssue false
  • English
  • Français

On Scott and Karp trees of uncountable models

Published online by Cambridge University Press:  12 March 2014

Tapani Hyttinen  and
Jouko Väänänen
Tapani Hyttinen
Affiliation:
Department of Mathematics, University of Helsinki, 00100 Helsinki, Finland
Jouko Väänänen
Affiliation:
Department of Mathematics, University of Helsinki, 00100 Helsinki, Finland
Get access Rights & Permissions [Opens in a new window]

Abstract

Let and 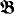be two countable relational models of the same first order language. If the models are nonisomorphic, there is a unique countable ordinal α with the property that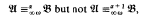

i.e. and 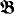are L∞ω-equivalent up to quantifier-rank α but not up to α + 1. In this paper we consider models and 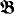of cardinality ω1 and construct trees which have a similar relation to and 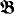as a above. For this purpose we introduce a new ordering T ≪ T′ of trees, which may have some independent interest of its own. It turns out that the above ordinal α has two qualities which coincide in countable models but will differ in uncountable models. Respectively, two kinds of trees emerge from α. We call them Scott trees and Karp trees, respectively. The definition and existence of these trees is based on an examination of the Ehrenfeucht game of length ω1 between and 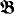. We construct two models of power ω1 with mutually noncomparable Scott trees.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 55 , Issue 3 , September 1990 , pp. 897 - 908
Copyright
Copyright © Association for Symbolic Logic 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Bar] Barwise, J., Admissible sets and structures, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
[Bau] Baumgartner, J., Harrington, L. and Kleinberg, E., Adding a closed unbounded set, this Journal, vol. 41 (1976), pp. 481–482.Google Scholar
[Hin] Hintikka, J. amd Rantala, V., A new approach to infinitary languages, Annals of Mathematical Logic, vol. 10 (1976), pp. 95–115.CrossRefGoogle Scholar
[Hytl] Hyttinen, T., Games and infinitary languages, Annales Academiae Scientiarum Fennicae Series A I: Mathematica Dissertationes, vol. 64 (1987).Google Scholar
[Hyt2] Hyttinen, T., Model theory for infinite quantifier languages, Fundamenta Mathematicae (to appear).Google Scholar
[Jech] Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[Kar] Karttunen, M., Syntax and semantics of infinitely deep languages, Annales Academiae Scientiarum Fennicae Series A I: Mathematica Dissertationes, vol. 50 (1984).Google Scholar
[Kue] Kueker, D., Countable approximations and Löwenheim-Skolem theorems, Annals of Mathematical Logic, vol. 11 (1977), pp. 57–103.CrossRefGoogle Scholar
[Nad] Nadel, M. and Stavi, J., L∞λ-equivalence, isomorphism and potential isomorphism, Transactions of the American Mathematical Society, vol. 236 (1978), pp. 51–74.Google Scholar
[Tod] Todorčević, S., Stationary sets, trees and continuums, Publications de l' institut Mathématique, Nouvelle Série, vol. 29 (43) (1981), pp. 249–262.Google Scholar