Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T08:12:22.770Z Has data issue: false hasContentIssue false
  • English
  • Français

On skinny stationary subsets of

Published online by Cambridge University Press:  12 March 2014

Yo Matsubara  and
Toshimichi Usuba
Yo Matsubara
Affiliation:
Graduate School of Information Science, Nagoya University, Furo-Cho, Chikusa-Ku, Nagoya, 464-8601, Japan, E-mail:yom@math.nagoya-u.ac.jp
Toshimichi Usuba
Affiliation:
Institute for Advanced Research, Nagoya University, Furo-Cho, Chikusa-Ku, Nagoya, 464-8601, Japan, E-mail:usuba@math.cm.is.nagoya-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notion of skinniness for subsets of and its variants, namely skinnier and skinniest. We show that under some cardinal arithmetical assumptions, precipitousness or 2λ-saturation of NSκλ ∣ X, where NSκλ denotes the non-stationary ideal over , implies the existence of a skinny stationary subset of X. We also show that if λ is a singular cardinal, then there is no skinnier stationary subset of . Furthermore, if λ is a strong limit singular cardinal, there is no skinny stationary subset of . Combining these results, we show that if λ is a strong limit singular cardinal, then NSκλ ∣ X can satisfy neither precipitousness nor 2λ-saturation for every stationary X ⊆ . We also indicate that 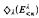, where 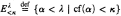, is equivalent to the existence of a skinnier (or skinniest) stationary subset of under some cardinal arithmetical hypotheses.

Keywords

non-stationary idealprecipitous idealsaturated ideal
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 2 , June 2013 , pp. 667 - 680
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Devlin, K. J., Constructibility, Springer-Verlag, 1984.CrossRefGoogle Scholar
[2]Foreman, M., Magidor, M., and Shelah, S., Martins maximum, saturated ideals, and nonregular ultrafilters. I, Annals of Mathematics. Series 2, vol. 127 (1988), no. 1, pp. 1–47.CrossRefGoogle Scholar
[3]Galvin, G., Jech, T. J., and Magidor, M., An ideal game, this Journal, vol. 43 (1978), no. 2, pp. 284–292.Google Scholar
[4]Jech, T. J., Some combinatorial problems concerning uncountable cardinals. Annals of Mathematical Logic, vol. 5 (1972/1973), pp. 165–198.CrossRefGoogle Scholar
[5]Jech, T. J., Set theory, third millennium, revised and expanded ed., Springer-Verlag, 2003.Google Scholar
[6]Kanamori, A., The higher infinite. Large cardinals in set theory from their beginnings, Springer-Verlag, 1994.Google Scholar
[7]Matet, P. and Shelah, S., The nonstationary ideal on Pκ(λ) for λ singular, preprint.Google Scholar
[8]Matsubara, Y. and Sakai, H., On the existence of skinny stationary sets, in preparation.Google Scholar
[9]Matsubara, Y. and Shelah, S., Nowhere precipitousness of the non-stationary ideal over , Journal of Mathematical Logic, vol. 2 (2002), no. 1, pp. 81–89.CrossRefGoogle Scholar
[10]Matsubara, Y. and Shioya, M., Nowhere precipitousness of some ideals, this Journal, vol. 63 (1998), no. 3, pp. 1003–1006.Google Scholar
[11]Shelah, S., The existence of coding sets, Around classification theory of models, ch. 7, Lecture Notes in Mathematics 1182, Springer, 1986, pp. 188–202.CrossRefGoogle Scholar
[12]Usuba, T., The non-stationary ideal over , doctoral dissertation, Nagoya University, 2008.Google Scholar