Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T13:30:43.886Z Has data issue: false hasContentIssue false
  • English
  • Français

On the bounded monadic theory of well-ordered structures

Published online by Cambridge University Press:  12 March 2014

Wolfgang Thomas
Wolfgang Thomas*
Affiliation:
Mathematisches Institut der Universität Freiburg, Freiburg, Federal Republic of Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Monadic (second-order) theories of well-orderings were first studied by Büchi [1], [2], [3] using concepts of automata theory. There it was shown that the monadic theory of ω, the monadic theory of any countable ordinal, and the monadic theory of ω1 are decidable. Expansions of the well-ordering (ω, <) by further relations were considered in [4], [5], [8] and [9], for example. Concerning such expansions, Buchi and Landweber [4] asked whether there is a set P ⊂ ω such that the weak monadic theory of (ω, <, P) is decidable and the (strong) monadic theory of (ω, <, P) is undecidable. In this note we give a negative answer by proving the following general theorem: If α is an ordinal and 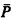an n-tuple of subsets of α, then the monadic theory of (α, <, 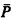) is decidable provided the monadic theory of (cf (α), <), i.e. of the cofinality of α, and the bounded monadic theory of (or, <, 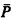) are decidable. (In the bounded monadic theory the second-order variables range only over bounded subsets of α.) Also we show that in the bounded and the (strong) monadic theory of a structure (α, <, 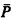) the same classes of subsets of α are definable. For the proofs we use a result of Shelah [7] and a suitable version of a combinatorial argument which was introduced by Büchi [1] and McNaughton [6] into the study of monadic theories.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 45 , Issue 2 , June 1980 , pp. 334 - 338
Copyright
Copyright © Association for Symbolic Logic 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Büchi, J. R., On a decision method in restricted second order arithmetic, Proceedings of the International Congress of Logic, Methodology and Philosophy of Science, 1960, Stanford University Press, Stanford, California, 1962, pp. 1–11.Google Scholar
[2]Büchi, J. R., Transfinite automata recursions and weak second order theory of ordinals, Proceedings of the International Congress of Logic, Methodology and Philosophy of Sciences, 1964, North-Holland, Amsterdam, 1965, pp. 3–23.Google Scholar
[3]Büchi, J. R., The monadic theory of all countable ordinals, Lecture Notes in Mathematics, vol. 328, Springer, Berlin, 1973, pp. 1–126.Google Scholar
[4]Büchi, J. R. and Landweber, L. H., Definability in the monadic second-order theory of successor, this Journal, vol. 34 (1969), pp. 166–170.Google Scholar
[5]Elgot, C. C. and Rabin, M. O., Decidability and undecidability of extensions of second (first) order theories of (generalized) successor, this Journal, vol. 31 (1966), pp. 169–181.Google Scholar
[6]McNaughton, R., Testing and generating infinite sequences by a finite automaton, Information and Control, vol. 9 (1966), pp. 521–530.CrossRefGoogle Scholar
[7]Shelah, S., The monadic theory of order, Annals of Mathematics, vol. 102 (1975), pp. 379–419.CrossRefGoogle Scholar
[8]Siefkes, D., Undecidable extensions of monadic second order successor arithmetic, Zeitschrift für Mathemattsche Logik und Grundlagen der Mathematlk, vol. 17 (1971), pp. 385–394.CrossRefGoogle Scholar
[9]Thomas, W., A note on undecidable extensions of monadic second order successor arithmetic, Archiv für Mathemattsche Logik und Grundlagensforschung, vol. 17 (1975), pp. 43–44.CrossRefGoogle Scholar