Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cantini, Andrea
2011.
Extending constructive operational set theory by impredicative principles.
Mathematical Logic Quarterly,
Vol. 57,
Issue. 3,
p.
299.
SATO, Kentaro
2015.
A new model construction by making a detour via intuitionistic theories II: Interpretability lower bound of Feferman's explicit mathematics T0.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 7-8,
p.
800.
Rathjen, Michael
2017.
Feferman on Foundations.
Vol. 13,
Issue. ,
p.
385.
Berger, Ulrich
and
Petrovska, Olga
2018.
Sailing Routes in the World of Computation.
Vol. 10936,
Issue. ,
p.
70.
Rathjen, Michael
and
Tupailo, Sergei
2020.
The Legacy of Kurt Schütte.
p.
377.
Berger, Ulrich
and
Tsuiki, Hideki
2021.
Intuitionistic fixed point logic.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 3,
p.
102903.
Curzi, Gianluca
and
Das, Anupam
2023.
Computational expressivity of (circular) proofs with fixed points.
p.
1.

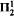 –CA
–CA