Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Harris, Charles M.
2012.
Badness and jump inversion in the enumeration degrees.
Archive for Mathematical Logic,
Vol. 51,
Issue. 3-4,
p.
373.
Elwes, Richard
Lewis-Pye, Andy
Löwe, Benedikt
Macpherson, Dugald
Normann, Dag
Sorbi, Andrea
Soskova, Alexandra A.
Soskova, Mariya I.
van Emde Boas, Peter
Wainer, Stan
and
Löwe, Benedikt
2018.
S. Barry Cooper (1943–2015).
Computability,
Vol. 7,
Issue. 2-3,
p.
103.

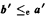 and
and 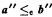 . This allows us to deduce, from results on the high/low jump hierarchy in the local Turing degrees and the jump preserving properties of the standard embedding
. This allows us to deduce, from results on the high/low jump hierarchy in the local Turing degrees and the jump preserving properties of the standard embedding 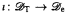 , that there exist Σ
, that there exist Σ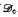 .
.