On the Kleene degrees of Π ₁ ¹ sets

Abstract

Let A and B be subsets of the reals. Say that A _K ≥ B, if there is a real a such that the relation “x ∈ B” is uniformly ⊿₁ (a, A) in 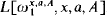. This reducibility induces an equivalence relation ≡ _K on the sets of reals; the ≡ _K -equivalence class of a set is called its Kleene degree. Let 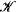be the structure that consists of the Kleene degrees and the induced partial order 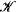≥. A substructure of 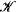that is of interest is 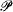, the Kleene degrees of the 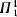sets of reals. If sharps exist, then there is not much to 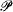, as Steel [9] has shown that the existence of sharps implies that 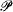has only two elements: the degree of the empty set and the degree of the complete 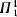set. Legrand [4] used the hypothesis that there is a real whose sharp does not exist to show that there are incomparable elements in 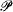; in the context of V = L, Hrbáček has shown that 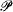is dense and has no minimal pairs. The Hrbáček results led Simpson [6] to make the following conjecture: if V = L, then 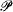forms a universal homogeneous upper semilattice with 0 and 1. Simpson's conjecture is shown to be false by showing that if V = L, then Gödel's maximal thin 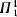set is the infimum of two strictly larger elements of .

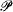The second main result deals with the notion of jump in 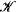. Let A′ be the complete Kleene enumerable set relative to A. Say that A is low-n if A ⁽ⁿ⁾ has the same degree as ⊘⁽ⁿ⁾, and A is high-n if A⁽ⁿ⁾ has the same degree as ⊘⁽ⁿ⁺¹⁾. Simpson and Weitkamp [7] have shown that there is a high (high-1) incomplete 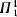set in L. They have also shown that various other 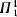sets are neither high nor low in L. Legrand [5] extended their results by showing that, if there is a real x such that x^# does not exist, then there is an element of 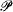that, for all n, is neither low-n nor high-n. In §2, ZFC is used to show that, for all n, if A is 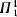and low-n then A is Borel. The proof uses a strengthened version of Jensen's theorem on sequences of admissible ordinals that appears in [7, Simpson-Weitkamp].