Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-11T06:02:35.706Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of nonisomorphic models of an infinitary theory which has the infinitary order property. Part A

Published online by Cambridge University Press:  12 March 2014

Rami Grossberg  and
Saharon Shelah
Rami Grossberg*
Affiliation:
Department of Mathematics, Ohio State University, Columbus, Ohio 43210
Saharon Shelah
Affiliation:
Institute of Mathematics, The Hebrew University, Jerusalem, Israel
*
Current address of R. Grossberg: Department of Mathematics, Rutgers University, New Brunswick, N.J. 08903
Get access Rights & Permissions [Opens in a new window]

Abstract

Let κ and λ be infinite cardinals such that λ ≤ λ (we have new information for the case when κ ≤ λ). Let T be a theory in Lκ +, ω of cardinality at most κ, let 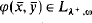. Now define

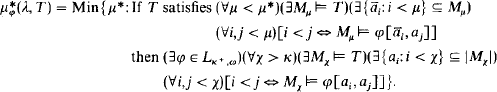
Our main concept in this paper is 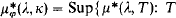is a theory in Lκ +, ω of cardinality κ at most, and φ(x, y) ϵ Lκ +, ω }. This concept is interesting because of

Theorem 1. Let T ⊆ Lκ +, ω of cardinality ≤ κ, and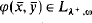 . If

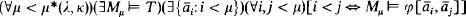
then (∀χ > κ)I(χ, T) = 2 χ (where I(χ, T) stands for the number of isomorphism types of models of T of cardinality χ).

Many years ago the second author proved that 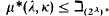. Here we continue that work by proving

Theorem 2. .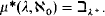

Theorem 3. For every κ ≤ λ we have .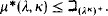

For some κ or λ we have better bounds than in Theorem 3, and this is proved via a new two cardinal theorem.

Theorem 4. For every T ⊆ Lκ +, ω, and any set of formulas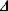 ⊆ Lκ +, ω such that 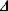T ⊇ Lκ +, ω, if T is (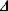, μ)-unstable for μ satisfying μμ*(λ,κ) = μ then T is 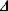-unstable (i.e. for every χ ≥ λ, T is (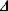, χ)-unstable). Moreover, T is Lκ +, ω-unstable.

In the second part of the paper, we show that always in the applications it is possible to replace the function I(χ, T) by the function IE(χ, T), and we give an application of the theorems to Boolean powers.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 2 , June 1986 , pp. 302 - 322
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

We would like to thank the United States-Israel Binational Science Foundation for partially supporting this research. We are grateful to the referee for a very long and detailed referee report. The first author received support from Harvey Friedman, whom he thanks.

References

REFERENCES

[BK] Barwise, Jon and Kunen, Kenneth, Hanf numbers for fragments of L∞,ω , Israel Journal of Mathematics, vol. 10 (1971), pp. 306–320.CrossRefGoogle Scholar
[Ch] Chang, C. C., Some remarks on the model theory of infinitary languages, The syntax and semantics of infinitary languages (Barwise, J., editor), Springer-Verlag, Berlin, 1968, pp. 36–63.CrossRefGoogle Scholar
[CK] Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[Di] Dickmann, M. A., Large infinitary languages, North-Holland, Amsterdam, 1975.Google Scholar
[GSh1] Grossberg, Rami and Shelah, Saharon, On the number of nonisomorphic models of an infinitary theory which has the infinitary order property, Abstracts of Papers Presented to the American Mathematical Society, vol. 5 (1984), p. 199 (abstract 84T-03-168).Google Scholar
[GSh2] Grossberg, Rami and Shelah, Saharon, On the number of nonisomorphic models of an infinitary theory which has the infinitary order property. Part B, submitted to this Journal.Google Scholar
[GSh3] Grossberg, Rami and Shelah, Saharon, More on the number of nonisomorphic models of an infinitary theory which has the infinitary order property, Abstracts of Papers Presented to the American Mathematical Society, vol. 5 (1984), p. 227 (abstract 84T-03-210).Google Scholar
[GSh4] Grossberg, Rami and Shelah, Saharon, A nonstructure theorem for an infinitary theory which has the unsuperstability property, submitted for the special issue of the Illinois Journal of Mathematics dedicated to the memory of W. W. Boone.Google Scholar
[Ho] Hodges, Wilfrid, On constructing many non-isomorphic algebras, Universal algbra and its links with logic, algebra, combinatorics and computer science (Burmeister, P. et al., editors), Heldermann Verlag, Berlin, 1984, pp. 67–77.Google Scholar
[Je] Jech, Thomas, Set theory, Academic Press, New York, 1978.Google Scholar
[Ke1] Keisler, H. Jerome, Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[Ke2] Keisler, H. Jerome, Some model theoretic results for ω-logic, Israel Journal of Mathematics, vol. 4 (1966), pp. 249–261.CrossRefGoogle Scholar
[Ma] Mansfield, R., The theory of Boolean ultrapowers, Annals of Mathematical Logic, vol. 2 (1970/1971), pp. 279–323.Google Scholar
[Mol] Morley, Michael D., Omitting classes of elements, The theory of models (Addison, J. W. et al., editors), North-Holland, Amsterdam, 1965, pp. 265–274.Google Scholar
[MSh] Macintyre, Angus and Shelah, Saharon, Uncountable universal locally finite groups, Journal of Algebra, vol. 43 (1976), pp. 168–175.CrossRefGoogle Scholar
[Sh0] Shelah, Saharon, Finite diagrams stable in power, Annals of Mathematical Logic, vol. 2 (1970/1971), pp. 69–118.CrossRefGoogle Scholar
[Sh1] Shelah, Saharon, The number of nonisomorphic models of an unstable first order theory, Israel Journal of Mathematics, vol. 9 (1971), pp. 473–487.CrossRefGoogle Scholar
[Sh2] Shelah, Saharon, A combinatorial problem: stability and order for models and theories in infinitary languages, Pacific Journal of Mathematics, vol. 41 (1972), pp. 247–261.CrossRefGoogle Scholar
[Sh3] Shelah, Saharon, The spectrum problem. I: ℵ ε -saturated models, the main gap, Israel Journal of Mathematics, vol. 43 (1982), pp. 324–356.CrossRefGoogle Scholar
[Sh4] Shelah, Saharon, Classification theory and the number of nonisomorphic models, North-Holland, Amsterdam, 1978.Google Scholar
[Sh4a] Shelah, Saharon, Classification theory and the number of nonisomorphic models, 2nd rev. ed., North-Holland, Amsterdam (to appear).Google Scholar
[Sh5] Shelah, Saharon, Constructions of many complicated uncountable structures and Boolean algebras, Israel Journal of Mathematics, vol. 45 (1983), pp. 100–146.CrossRefGoogle Scholar
[Sh6] Shelah, Saharon, Stability, the f.c.p., and superstability: model theoretic properties of formulas in first order theory, Annals of Mathematical Logic, vol. 3 (1971), pp. 271–362.CrossRefGoogle Scholar
[ShZ] Shelah, Saharon and Ziegler, Martin, Algebraically closed groups of large cardinality, this Journal, vol. 44 (1979), pp. 522–532.Google Scholar