Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Glaß, Thomas
1995.
Understanding uniformity in Feferman's explicit mathematics.
Annals of Pure and Applied Logic,
Vol. 75,
Issue. 1-2,
p.
89.
Glaß, Thomas
and
Strahm, Thomas
1996.
Systems of explicit mathematics with non-constructive μ-operator and join.
Annals of Pure and Applied Logic,
Vol. 82,
Issue. 2,
p.
193.
Rüede, Christian
2003.
The proof-theoretic analysis of Σ11 transfinite dependent choice.
Annals of Pure and Applied Logic,
Vol. 122,
Issue. 1-3,
p.
195.
Kahle, Reinhard
2003.
Universes over Frege structures.
Annals of Pure and Applied Logic,
Vol. 119,
Issue. 1-3,
p.
191.
Wilkie, Alex J.
2009.
2008 European Summer Meeting of the Association for Symbolic Logic. Logic Colloquium '08.
The Bulletin of Symbolic Logic,
Vol. 15,
Issue. 1,
p.
95.
Freund, Anton
and
Rathjen, Michael
2021.
Derivatives of normal functions in reverse mathematics.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 2,
p.
102890.
Sato, Kentaro
2023.
A new model construction by making a detour via intuitionistic theories III: Ultrafinitistic proofs of conservations of Σ11 collection.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 3,
p.
103207.

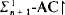 and
and 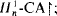 ; the proof does not use Skolem theories.
; the proof does not use Skolem theories.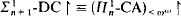 , for suitable classes of sentences;
, for suitable classes of sentences;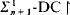 proves the consistency of
proves the consistency of 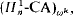 , for finite
, for finite 