Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cooper, S. Barry
1990.
Recursion Theory Week.
Vol. 1432,
Issue. ,
p.
57.
1992.
Vol. 125,
Issue. ,
p.
603.
Sorbi, Andrea
2009.
Theory and Applications of Models of Computation.
Vol. 5532,
Issue. ,
p.
29.
Casalegno, Paolo
2009.
Reasons to Believe and Assertion.
Dialectica,
Vol. 63,
Issue. 3,
p.
231.

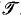 , ≤ 〉 be the usual structure of the degrees of unsolvability and 〈
, ≤ 〉 be the usual structure of the degrees of unsolvability and 〈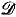 , ≤ 〉 the structure of the
, ≤ 〉 the structure of the 