No CrossRef data available.
Article contents
On the undecidability of finite planar cubic graphs1
Published online by Cambridge University Press: 12 March 2014
Extract
In the March, 1971 issue of this Journal [1] a paper of ours was published purporting to prove the hereditary undecidability of the first-order theory of finite planar graphs. The proof presented there contains an error which is unfortunately “unfixable” by the methods of that paper. The theorem however is true and we demonstrate here a generalization to finite cubic (exactly three edges at each vertex) planar graphs. The method involves coding the halting problem for a Turing machine into the theory of these graphs by considering special printouts of computations. Let us first consider a discussion of the aforementioned mistake and see what can be learned from it.
By a graph 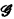 we will mean a nonempty set V of points together with a set I of unordered pairs of points of V. Each point i = {u, v) ∈ I is an edge of
we will mean a nonempty set V of points together with a set I of unordered pairs of points of V. Each point i = {u, v) ∈ I is an edge of 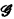 A graph is called finite if ∣V∣ is finite. A graph is said to be planar iff it can be embedded in the plane (i.e., drawn in the plane so that no two edges intersect).
A graph is called finite if ∣V∣ is finite. A graph is said to be planar iff it can be embedded in the plane (i.e., drawn in the plane so that no two edges intersect).
In the earlier paper the method of proof was a semantic embedding of certain binary relations into finite planar graphs. The essential idea was, for a given relation, to let the vertices of the graph interpret the field of the relation and the edges represent the related pairs. This method works for arbitrary graphs, but in the planar case has two main difficulties.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
Footnotes
The authors would like to thank Professor Michael Morley for his many helpful conversations which led to the preparation of this paper.

