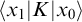ON ULTRAPRODUCTS, THE SPECTRAL THEOREM AND RIGGED HILBERT SPACES

Abstract

We start by showing how to approximate unitary and bounded self-adjoint operators by operators in finite dimensional spaces. Using ultraproducts we give a precise meaning for the approximation. In this process we see how the spectral measure is obtained as an ultralimit of counting measures that arise naturally from the finite dimensional approximations. Then we see how generalized distributions can be interpreted in the ultraproduct. Finally we study how one can calculate kernels of operators K by calculating them in the finite dimensional approximations and how one needs to interpret Dirac deltas in the ultraproduct in order to get the kernels as propagators $\langle x_{1}|K|x_{0}\rangle $.

1 Introduction

This paper continues a study of finite dimensional approximations of operators on Hilbert spaces. We started the work in [6], motivated by a quest for mathematically justified eigenvectors in quantum mechanics. There we built eigenvectors directly as ultraproducts of eigenvectors in the small spaces. This time we look at another way of finding finite dimensional approximations, and reconstruct the spectral decomposition theorem using ultraproducts. We also find structure resembling rigged Hilbert spaces, thus providing generalized eigenvectors and bringing us back to our earlier motivation.

In quantum mechanics the states of a system are usually represented by unit vectors in a Hilbert space. Observables of the system are modeled by self-adjoint (often unbounded) operators whose spectrum gives the possible measurement outcomes. If the observable has a finite spectrum and a finite number of eigenvectors, this model coincides with Dirac’s bra- and ket-vector representation [3], but in general Dirac’s bras and kets don’t form a Hilbert space. A key ingredient in Dirac’s approach, the delta-functions, were later mathematically justified by Schwartz [10] as distributions, functionals over a set of test functions. Gelfand and Vilenkin [4] found a natural space for these, namely the rigged Hilbert spaces. These are triplets of spaces: in addition to a Hilbert space, one considers a dense subspace of it—the test functions—and the space of either linear or antilinear functions over these test functions. This last space, in which the Hilbert space embeds naturally, is the space of distributions. The linear functions correspond to bra vectors, the antilinear functions to ket vectors.

One key question about quantum systems is how they evolve over time. Depending on the approach to the system, this is described either by the kernel of the time evolution operator, or via the Feynman propagator. The kernel is a function $K(x,y)$ such that the action of the time evolution operator K on a wave function $\varphi $ can be described by

$$ \begin{align*}K(\varphi)(y)=\int_S K(x,y)\varphi(x)d\mu(x), \end{align*} $$

where S is the spectrum of the observable.

We study a method of calculating the kernel via the finite dimensional approximations. Although our method builds on ultraproducts, the space studied is not the full ultraproduct, but a subspace of it. As this is not elementary, we cannot use Łos’s theorem, but this is not a problem: as we are only interested in equations, it is enough to have just an embedding of the original space into the ultraproduct space. This also means that our approach does not restrict to only pseudocompact spaces (the metric analogue of pseudofinite spaces, see [5]).

Discrete approximations of quantum systems have been used and studied extensively in physics. From the list of references of [6] one can find examples of this. They have been studied also in mathematical physics, see, e.g., [1]. We got inspired by the work of B. Zilber [12], and set out to compute concrete examples of kernels in [6]. The question we studied there was whether it is possible to calculate the kernels of the time evolution operators by calculating them in some kind of finitely generated approximations of quantum systems which in [6] were the free particle and the harmonic oscillator. It turned out that in these cases it is possible. One can choose the approximations to be simply finite dimensional Hilbert spaces with rather straightforward approximations of the position operator and the momentum operator. In the choice of the approximations of the time evolution operator one needed to be more creative in the case of the harmonic oscillator. To determine in which sense the approximations approximate the quantum systems was more tricky. For that we used a rather heavily modified version of the metric ultraproduct of the finite dimensional Hilbert spaces. Once we knew how the approximation works, it was rather straightforward to do the calculations with the help of number theory.

However, following Zilber, we would have liked to be able to calculate the kernels by using Dirac deltas in the propagator style $\langle x_{1}|K|x_{0}\rangle $ . In [6] our interpretation of Dirac deltas was as ultraproducts of eigenvectors. In hind sight that was too naive an approach, and didn’t work out. The propagators calculated in the finite dimensional models did not give a correct propagator in the ultraproduct, and not even some kind of ad hoc renormalization would have made the values correct, as there were also divisibility-related discretizing effects stemming from the finite approximations. The remedy in [6] was to calculate the kernel instead, as this could be done using the propagators in the finite dimensional models, and the method ‘averaged out’ the discretization effect.

In this paper we continue the work we started in [6], but we look at a general case instead of concrete examples. Also, the method is different. The first question we look at is the following: Given a separable Hilbert space H and an operator A on it, can one find finite dimensional Hilbert spaces $H_{N}$ and operators $A_{N}$ on them so that the operators approximate A in the sense that H with A is isometrically isomorphic to a submodel of the metric ultraproduct of the spaces $H_{N}$ with operators $A_{N}$ ? The first problem in finding the pairs $(H_{N},A_{N})$ is that in the case where the operator A is unbounded, the metric ultraproduct $A^{m}$ of the operators $A_{N}$ can not be well-defined everywhere in the metric ultraproduct $H^{m}$ of the spaces $H_{N}$ . In [6] looking at the position and momentum operators, we were able to show that $A^{m}$ is well defined in a suitable part of $H^{m}$ so that the isomorphism can indeed be found. In this paper we look only at bounded operators and thus this problem does not arise. Although this does restrict the direct applicability of our method, we hope the method can be extended, more on this below.

In sections 2 and 3 we consider the approximation question in the case where A is such that $AA^{*}=A^{*}A=rI$ where r is a positive real and I is the identity operator. So, e.g., A can be a unitary operator. We show how the operators $A_{N}$ can be found, show how the spectral measure $\mu $ for A is obtained as an ultralimit of counting measures that arise from the approximations naturally, and how the approximations give A as a multiplication operator in the space $L_{2}(\sigma (A),\mu )$ .

In the fouth section we study the same questions for bounded self-adjoint operators A and get the same results by reducing the questions to the previous case by looking at the operator $e^{irA}$ for r a small enough real.

In the fifth section we look at generalized distributions in the context of the space $L_{2}(\sigma (A),\mu )$ from the previous sections. See [9] for the classical theory of generalized distributions. Now the generalized distributions (excluding some) cannot be seen as elements of $H^{m}$ . Thus we look at the space $H^{\infty }$ which is obtained from the classical ultraproduct of the spaces $H_{N}$ by fractioning out the equivalence relation of being infinitely close to each other in a metric that arises from the norms in $H_N$ . This space contains infinite vectors giving us a chance. The problem here is that the ultraproduct of the inner products in the spaces $H_{N}$ is not well-defined everywhere in $H^{\infty }\times H^{\infty }$ . It turns out that it is well defined in a large enough subset so that one can interpret generalized distributions $\theta $ as vectors $u(\theta )$ in $H^{\infty }$ so that for all continuous $f:\sigma (A)\rightarrow \mathbb {C}$ , where $\mathbb {C}$ is the field of complex numbers, $\theta (f)=\langle F^m(f)|u(\theta )\rangle $ where $F^m$ is a natural embedding we get from the isometric embedding of $L_{2}(\sigma (A),\mu )$ into $H^{m}$ , see above (the embedding is not into $H^{\infty }$ , for details see Section 4).

In the sixth section we look at ways of calculating the kernel of an operator B on $L_{2}(\sigma (A),\mu )$ (or on H). We start by showing that the method from [6] works also here assuming that we can find reasonable approximations $B_{N}$ for B in the spaces $H_{N}$ . In [6] we showed how to find these for the time evolution operators B of the free particle and the harmonic oscillator (there A was the position operator). Here we show that if B has a kernel, then the reasonable approximations $B_{N}$ can always be found. However, unlike in the special cases studied in [6], here our proof is essentially existential and does not give a practical way of finding the approximations. One must keep in mind that finding the kernels is difficult and thus one can not expect to have a simple trick that gives them.

In the sixth section we also show that the kernel can be obtained as the propagator $\langle x_{1}|B|x_{0}\rangle $ (using the discrete approximations we can extend B to an operator that acts also on Dirac deltas) if one is very careful in choosing the interpretations of the Dirac deltas $|x_{1}\rangle $ and $|x_{0}\rangle $ and here, of course, we think of Dirac deltas as generalized distributions as is common in mathematics. The need to be very careful comes from the fact that $\langle x_{1}|B|x_{0}\rangle $ is very sensitive to the choice of eigenvectors, as opposed to $\langle F^m(f)|u(\theta )\rangle $ . In [6] we showed that a straightforward approach to eigenvectors can give completely wrong values. As the result, this Dirac delta method is probably not very practical if applied in a straightforward manner. From [8] one can find an example of a rigorous use of Dirac deltas in the context where Dirac deltas are interpreted as generalized distributions.

Open question 1. Can one find approximations $A_{N}$ for bounded normal operators A or unbounded self adjoint operators?

Although it is not immediate, we believe that if one can find finite dimensional approximations of bounded normal operators, one can combine the classical trick of looking at the operators $(A\pm iI)^{-1}$ and our technique for building unbounded operators in ultraproducts from [6] to find approximations for unbounded self-adjoint operators. However, even in the case of bounded normal operators we have a serious problem: How to find the approximations $A_{N}$ so that they are roughly like how we chose them in Section 1 and still normal. (With the assumption $AA^{*}=A^{*}A=rI$ , there are no problems in guaranteeing normality, in fact, this assumption was designed to get normal approximations.) The conventional trick of decomposing normal operators into two commuting self-adjoint ones does not seem to work directly, as building approximations for them in the spaces $H_N$ seems to destroy commutativity. However, our current understanding is that there may be a remedy to this.

2 The construction

This section presents the basic construction of finite-dimensional approximations that we will use and modify in later sections. Here we study a separable Hilbert space with a (scaled) unitary operator having a cyclic vector. We use the cyclic vector and polynomials to build finite-dimensional approximations such that the original Hilbert space embeds isometrically into their metric ultraproduct. We also get a vector space homomorphism from the space of polynomials (over a compact set $S\subset \mathbb {C}$ ) into the metric ultraproduct. In Section 3 we will construct a suitable measure to make the homomorphism an isometry.

The construction will be used to find similar approximations for the case where the operator is bounded and self-adjoint in Section 4. In Section 5 we will study other norms for the ultraproduct space that will be essential in studying distributions in Sections 5 and 6. In Section 7 we will have a short look at what one can do if the operator doesn’t have a cyclic vector.

So we let H be a separable complex Hilbert space and A an operator on H of the form $qU$ , where q is a nonzero complex number and U is unitary. Then A is normal and bounded and $A^{*}\circ A=A\circ A^{*}=r_{A}I$ where $r_{A}$ is a positive real, I is the identity operator, and $A^{*}$ is the adjoint of A. This is enough for the constructions we do in this paper (we will use the construction when A is unitary), but we use notation allowing for more general operators, as there are also other operators allowing for this sort of approximations (see the example at the end of this section).

From a polynomial $P(X,Y)\in \mathbb {C} [X,Y]$ over the complex numbers $\mathbb {C}$ we get an operator $P(A,A^{*})$ on H the natural way, e.g., $X^{2}Y(A,A^{*})=A\circ A\circ A^{*}$ , and we say that $\phi \in H$ is cyclic if the set $\{ P(A,A^{*})(\phi )\vert \ P\in \mathbb {C} [X,Y]\}$ is dense in H. We will here study the case where there is a cyclic vector $\phi $ in H and we pick $\phi $ so that in addition its norm is $1$ . Notice that H can always be split into countably many complete subspaces so that they are orthogonal to each other, closed under A and $A^{*}$ and each of them has a cyclic vector, and in Section 7 we will see how to combine the constructions from this decomposition.

For all $N\in {\omega }$ , let $H_{N}$ be the subspace of H generated by

(1) $$ \begin{align} \{A^{i}(A^{*})^{j}(\phi )\vert\ i\le N,\ j\le N\}. \end{align} $$

In particular, note that $H_0$ is the space generated by $\phi $ , and $H_N\subset H_{N+1}$ . Notice that as finite dimensional spaces these are complete spaces. We write $H^{-}_{N}$ for the subspace of H generated by

(2) $$ \begin{align} \{A^{i}(A^{*})^{j}(\phi )\vert\ i< N,\ j\le N\} \end{align} $$

and $H^{+}_{N}$ for the subspace of H generated by

(3) $$ \begin{align} \{A^{i}(A^{*})^{j}(\phi )\vert\ 0<i\le N,\ j\le N\}. \end{align} $$

As $AA^*=A^*A=r_AI$ , the operators A and $A^*$ swap these spaces: A maps $H^{-}_{N}$ onto $H^{+}_{N}$ and $A^{*}$ maps $H^{+}_{N}$ onto $H^{-}_{N}$ . To get approximating operators on $H_N$ we can modify A and $A^*$ by a wraparound trick: Let $W^{-}$ be the orthogonal complement of $H^{-}_{N}$ in $H_{N}$ and $W^{+}$ be the orthogonal complement of $H^{+}_{N}$ in $H_{N}$ . Then $W^{+}$ and $W^{-}$ have the same dimension and we let U be a unitary operator from $W^{-}$ onto $W^{+}$ . Now we define an operator $A_{N}$ on $H_{N}$ as follows. If $u\in H^{-}_{N}$ , then $A_{N}(u)=A(u)$ and if $u\in W^{-}$ , then $A_{N}(u)=\sqrt {r_{A}}U(u)$ (by $\sqrt {r_{A}}$ we mean the one that is positive). We get the adjoint of $A_{N}$ as follows: If $u\in H^{+}_{N}$ , then we let $A^{*}_{N}(u)=A^{*}(u)$ and if $u\in W^{+}$ , then $A^{*}_{N}(u)=\sqrt {r_{A}}U^{-1}(u)$ . It is easy to check that $A^{*}_{N}$ is indeed the adjoint of $A_{N}$ and that $A^{*}_{N}\circ A_{N}=A_{N}\circ A^{*}_{N}=r_{A}I$ and so $A_{N}$ is normal. Notice that because of how A and $A^*$ cancel out (up to multiplication by a constant), $H^{+}_{N}$ is also generated by the set $\{A^{i}(A^{*})^{j}(\phi )\vert \ i\le N,\ j< N\}$ . Thus $H_N^-$ and $H_N^+$ are the subspaces on which $A_N$ and $A_N^*$ respectively behave ‘correctly’ and

(4) $$ \begin{align} A_{N}(A^{i}(A^{*})^{j}(\phi))=A(A^{i}(A^{*})^{j}(\phi ))=A^{i+1}(A^{*})^{j}(\phi ) \textrm{ if } i<N,\,j\leq N \end{align} $$

and

(5) $$ \begin{align} A^{*}_{N}(A^{i}(A^{*})^{j}(\phi ))=A^{i}(A^{*})^{j+1}(\phi )\textrm{ if }j<N,\, i\leq N. \end{align} $$

In $H_{N}$ we can also define operators $P(A_{N},A_{N}^{*})$ for polynomials $P(X,Y)$ in the natural way.

For all $N\in {\omega }$ , we let $D_{N}$ be the dimension of $H_{N}$ and we choose eigenvectors $u_{N}(n)$ , $n<D_{N}$ , of $A_{N}$ with eigenvalues $\lambda _{N}(n)$ . Notice that

(6) $$ \begin{align} u_{N}(n)\ \text{is also an eigenvector of } A^{*}_N \text{ with eigenvalue } \overline{\lambda_{N}(n)}, \end{align} $$

where $\overline {\lambda _{N}(n)}$ is the complex conjugate of $\lambda _{N}(n)$ . Since $A_{N}$ is normal, we can choose these so that they form an orthonormal basis of $H_{N}$ . Denote $\xi _{N}(n)=\langle u_{N}(n) |\phi \rangle $ , i.e.,

(7) $$ \begin{align} \phi =\sum_{n=0}^{D_{N}-1}\xi_{N}(n)u_{N}(n), \end{align} $$

and we choose the vectors $u_{N}(n)$ so that in addition $\xi _{N}(n)$ is a non-negative real number. Then we have

(8) $$ \begin{align} A_N(\phi)=\sum_{n=0}^{D_{N}-1}\lambda_N(n)\xi_{N}(n)u_{N}(n)\ \text{and}\ A^*_N(\phi)=\sum_{n=0}^{D_{N}-1}\overline{\lambda_N(n)}\xi_{N}(n)u_{N}(n). \end{align} $$

One should note that even though the spaces $H_N$ form an increasing sequence, the bases do not extend each other, as the operators $A_N$ (as well as the operators $A_N^*$ ) do not extend each other (because of the wraparound modification).

Next we want to tie a spectral decomposition of A to our finite-dimensional approximation. So we choose a natural number M so that it is strictly greater than both the operator norm of A and $\sqrt {r_{A}}$ , and let

(9) $$ \begin{align} S=\{\lambda\in\mathbb{C}\vert\ -M\le Re(\lambda )\le M, -M\le Im(\lambda )\le M\}. \end{align} $$

Notice that there is a real $\varepsilon>0$ such that for all $N<{\omega }$ and $n<D_{N}$ , $\vert \lambda _{N}(n)\vert <M-\varepsilon $ since the norm of $A_{N}$ is at most the maximum of the norm of A and $\sqrt {r_{A}}$ . For all $X\subseteq \mathbb {C}$ , let $C(X)$ be the vector space of all bounded continuous functions from X to $\mathbb {C}$ . Of these our main interest is in $C(S)$ . Notice that since S is compact, every $f\in C(S)$ is uniformly continuous. We let $D(S)$ be the subspace of $C(S)$ that consists of all functions $f_{P}(\lambda )=P(\lambda ,\overline \lambda )$ , where $P\in \mathbb {C}[X,Y]$ and $\overline \lambda $ is the complex conjugate of $\lambda $ . On $D(S)$ we can again define operators $A_{D}$ and $A^{*}_{D}$ in a natural way

(10) $$ \begin{align} A_D(f_P)=f_{XP}\quad\text{and}\quad A^*_D(f_P)=f_{YP} \end{align} $$

(e.g., $A_{D}(f_{X^{i}Y^{j}})=f_{X^{i+1}Y^{j}}$ ). Notice that $A_{D}(f_{P})(\lambda )=\lambda f_{P}(\lambda )$ and $A^{*}_{D}(f_{P})(\lambda )=\overline \lambda f_{P}(\lambda )$ .

Let’s define some mappings that will be crucial in this paper:

Definition 2.1. We define $G: D(S)\to H$ and $F_N:D(S)\to H_N$ as follows: For $P\in \mathbb {C}[X,Y]$ , let

(11) $$ \begin{align} G(f_{P})=P(A,A^{*})(\phi ) \end{align} $$

and note that it is a homomorphism from $D(S)$ to H (as vector spaces), and that its image is dense in H (by the cyclicity assumption). Further let

(12) $$ \begin{align} F_{N}(f_{P})=\sum_{n<D_{N}}\xi_{N}(n)f_{P}(\lambda_{N}(n))u_{N}(n), \end{align} $$

and note by comparing to Equation (8) that $F_{N}(f_{P})=P(A_{N},A_{N}^{*})(\phi )$ , and also that this is a homomorphism from $D(S)$ to $H_{N}$ . Also note, that as $\lVert {A_N}\rVert $ is always bounded by $\max \{\lVert {A}\rVert ,\sqrt {r_A}\}$ , for each $f_P\in D(S)$ , $\{F_N(f_P):N\geq 1\}$ is bounded.

Now the inner product in $H_{N}$ (inherited from H), gives us one norm $\Vert \cdot \Vert _{2}$ on  $H_{N}$ . Using this, there is a natural way of defining metric ultraproducts of the Hilbert spaces $H_N$ . However, we want to consider also other norms in the ultraproduct, so we take as our starting point a classical ultraproduct of the structures $H_N$ and ‘dig out’ various metric ultraproduct spaces from it. We look at the $\lVert {\cdot }\rVert _2$ -norm here, and consider the other norms in Section 5.

Let ${\mathcal {U}}$ be a nonprincipal ultrafilter on ${\omega }$ . Depending on what one wishes to calculate using the finite dimensional approximations, here there is room to adjust the ultrafilter accordingly. For example, in [6] our calculations required that for all $m\in {\omega }-\{ 0\}$ , $\{ N\in {\omega } -\{ 0\}\vert \ \sqrt {N}\in {\omega } ,\ m|\sqrt {N}\}\in {\mathcal {U}}$ , and similar properties can be added according to need.

Let $H^{u}$ be the (classical) ultraproduct $\Pi _{N\in {\omega }}H_{N}/{\mathcal {U}}$ and $\mathbb {C}^{u}$ be the ultrapower $\mathbb {C}^{{\omega }}/{\mathcal {U}}$ of the field of complex numbers $\mathbb {C}$ . Then $H^{u}$ is a vector space over $\mathbb {C}^{u}$ and by identifying elements of $\mathbb {C}$ with their images under the canonical embedding of $\mathbb {C}$ into $\mathbb {C}^{u}$ , also a vector space over $\mathbb {C}$ . There is also a pairing $\langle \cdot |\cdot \rangle ^{u}$ from $H^{u}$ to $\mathbb {C}^{u}$ which is obtained as the ultraproduct of the inner products $\langle \cdot |\cdot \rangle _{N}$ of $H_{N}$ . And similarly we get a unary function $\Vert \cdot \Vert ^{u}_{2}$ . Notice that for all $v=(v_{N})_{N\in {\omega }}/{\mathcal {U}}\in H^{u}$ , $\Vert v\Vert ^{u}_{2}= (\sqrt {\langle v_{N}|v_{N}\rangle _{N}})_{N\in {\omega }}/{\mathcal {U}}$ and that $((\sqrt {\langle v_{N}|v_{N}\rangle _{N}})_{N\in {\omega }}/{\mathcal {U}})^{2}=\langle v\vert v\rangle ^{u}$ . Similarly for all $q=(q_{N})_{N\in {\omega }}/{\mathcal {U}}\in \mathbb {C}^{u}$ , we write $\vert q\vert ^{u}$ for $(\vert q_{N}\vert )_{N\in {\omega }}/{\mathcal {U}}$ . Notice that if we let X be the range of this ‘absolute value’, then $\mathbb {R}^{u}=X\cup \{-r\vert \ r\in X\}$ is a real closed field containing the reals. In particular, it is linearly ordered and thus we can compare, e.g., the ‘norm’ $\Vert v\Vert ^{u}$ of $v\in H^{u}$ and a rational number. Thus for all $u,v\in H^{u}$ , if there is $q\in \mathbb {C}$ such that q is infinitely close to $\langle u|v\rangle ^{u}$ , we write $\langle u\vert v\rangle $ for this q. If there is no such q, we write $\langle u|v\rangle =\infty $ .

Notation 2.2. When we define an element $(v_{N})_{N<{\omega }}/{\mathcal {U}}$ of $H^{u}$ , it is enough to define the vectors $v_{N}$ so that the definition makes sense for all N in some set that belongs to ${\mathcal {U}}$ . This often simplifies notation considerably.

Now $H^{u}$ contains some structures of interest to us. Let us first look at $H^{\infty }$ : On $H^{u}$ we define an equivalence relation $\sim $ so that $u\sim v$ if $\Vert u-v\Vert ^{u}_{2}$ is infinitesimal (i.e., smaller than $1/n$ for all natural numbers n) and let $H^{\infty }=H^{u}/\sim $ . Now addition of elements of $H^{\infty }$ and for all $q\in \mathbb {C}$ , the multiplication by q are well-defined in $H^{\infty }$ and thus $H^{\infty }$ is a vector space over $\mathbb {C}$ . We define a partial pairing $\langle \cdot |\cdot \rangle $ on $H^{\infty }$ as follows: For all $u,v\in H^{\infty }$ , if there is $q\in \mathbb {C}$ such that for all $u'\in u/\sim $ and $v'\in v/\sim $ , $\langle u'|v'\rangle ^{u}=q$ , then we let $\langle u|v\rangle =q$ and otherwise $\langle u|v\rangle $ is $\infty $ .

The second of these structures is the metric ultraproduct $H^{m}$ : We let $H^{m}$ be the set of all $v/\sim \in H^{\infty }$ such that $\Vert v\Vert ^{u}_{2}$ is finite (i.e., smaller than some natural number). Notice that $H^{m}$ is still a vector space over $\mathbb {C}$ and $\langle \cdot |\cdot \rangle $ is total on $H^{m}$ and, in fact, an inner product. This also gives a norm on $H^{m}$ but it is the same as $\Vert \cdot \Vert _{2}$ defined above. Later, when considering spaces arising from other norms, we may write $H^{m}_{2}$ for $H^{m}$ .

Remark 2.3. We could define $\sim $ also on $\mathbb {C}^{u}$ by $q\sim r$ if $\vert q-r\vert ^{u}$ is infinitesimal and let $\mathbb {C}^{\infty }$ be $\mathbb {C}^{u}/\sim $ . Notice that multiplication is not well defined in $\mathbb {C}^{\infty }$ if one of the elements has infinite norm. Then we could let $\mathbb {C}^{m}$ be (the field of) all $q/\sim \in \mathbb {C}^{\infty }$ such that $\vert q\vert ^{u}$ is finite. Notice that $\mathbb {C}^{m}=\{ q/\sim \vert \ q\in \mathbb {C}\}$ and that for all $u,v\in H^{m}$ , if $\langle u|v\rangle =q$ , then $q/\sim =\langle u|v\rangle ^{u}/\sim $ .

Let $A^{u}$ be the ultraproduct of the operators $A_{N}$ . Since the operators $A_{N}$ are uniformly bounded, $A^{u}$ induces a well-defined operator $A^{\infty }$ on $H^{\infty }$ and the restriction $A^{m}$ of $A^{\infty }$ to $H^{m}$ is a well-defined operator on $H^{m}$ . We can do the same for the $A^{*}_{N}$ ’s and get operators $A^{*u}$ , $A^{*\infty }$ and $A^{*m}$ . Notice that $(A^{m})^{*}=A^{*m}$ since being an adjoint is preserved in metric ultraproducts and that $A^{m}$ and $A^{*m}$ commute since $A_{N}$ and $A^{*}_{N}$ commute for all N and thus $A^{m}$ is normal.

Now the homomorphisms $F_N$ (from Definition 2.1) induce a homomorphism from the vector space $D(S)$ into $H^m$ :

Definition 2.4. Let $F^m: D(S)\to H^m$ be given by

$$ \begin{align*}F^m(f_{P})=(F_{N}(f_{P}))_{N<{\omega}}/{\mathcal{U}}/\sim .\end{align*} $$

This is well-defined, as $\{F_N(f_P):N<{\omega }\}$ is bounded (see Definition 2.1). By $F^u$ we will denote the homomorphism from $D(S)$ to $H^u$ :

$$ \begin{align*}F^u(f_{P})=(F_{N}(f_{P}))_{N<{\omega}}/{\mathcal{U}}.\end{align*} $$

Notice that $F^m(A_{D}(f_{P}))=A^{m}(F^m(f_{P}))$ and similarly for $A^{*}_{D}$ and $A^{*m}$ . We can also embed H into $H^m$ :

Definition 2.5. Let $G^m: H\to H^m$ be given by

$$ \begin{align*}G^{m}(P(A,A^{*})(\phi ))=(P(A,A^{*})(\phi ))_{N<{\omega}}/{\mathcal{U}}/\sim ,\end{align*} $$

and denote $H^{Im}=rng(G^m)$ .

Notice that $G^m$ is well-defined, as

$$ \begin{align*}P(A,A^{*})(\phi )\in H_{N}\end{align*} $$

for all N large enough. Notice also that for all $\psi \in H$ , $G^{m}(A(\psi ))=A^{m}(G^{m}(\psi ))$ and the same for $A^{*}$ and $A^{*m}$ . Also $\Vert G^{m}(\psi )\Vert ^{m}_{2}=\Vert \psi \Vert _{2}$ and so $G^{m}$ is an (isometric) embedding of the Hilbert space H into $H^{m}$ and maps A to $A^{m}\restriction H^{Im}$ and $A^{*}$ to $A^{*m}\restriction H^{Im}$ .

So we have seen the following:

Lemma 2.6. $G^{m}$ is an isometric isomorphism from H onto $H^{Im}$ , $G^{m}\circ A=A^{m}\circ G^{m}$ , $G^{m}\circ A^{*}=A^{*m}\circ G^{m}$ , and $A^{*m}$ and $A^{*m}\restriction H^{Im}$ are the adjoints of $A^{m}$ and $A^{m}\restriction H^{Im}$ , respectively.

Corollary 2.7. For all $f\in D(S)$ , $G^{m}(G(f))=F^m(f)$ .

Proof. Now $f=f_{P}$ for some $P\in \mathbb {C} [X,Y]$ . Then

$$ \begin{align*}G^{m}(G(f))=G^{m}(P(A,A^{*})(\phi ))=P(A^{m},A^{*m})(G^{m}(\phi ))=F^m(f),\end{align*} $$

where the last identity follows from (4), (5), and (6) above.

As we are working with several spaces and functions, we have gathered the main ones in Figure 1 to act as a quick reference.

Figure 1 The main spaces and functions.

We now return to the reason for talking about A and $A^*$ instead of A and $A^{-1}$ , namely there are operators that are not obtained just by multiplying a unitary operator by a constant but that still allow for the sort of approximation we developed here.

Example 2.8. Let $A=rU$ be an operator with a cyclic vector u on a Hilbert space $H_1$ and $B=qV$ be an operator with a cyclic vector v on a Hilbert space $H_2$ , where $r,q\in \mathbb {C}$ , $r,q\neq 0$ , $r\neq q$ , and U and V are unitary. Then consider the space $H\subset H_1\oplus H_2$ spanned by the vectors $(A\oplus B)^i(A^*\oplus B^*)^j(u\oplus v)$ , for $i,j<{\omega }$ . This gives a space (H) and an operator $(A\oplus B)$ with a cyclic vector ( $u\oplus v$ ) such that the operator is not a constant times a unitary operator, but one can still build spaces $H_N$ as above (generated by vectors $(A\oplus B)^i(A^*\oplus B^*)^j(u\oplus v)$ with $i,j\leq N$ ).

Open question 2. What exactly is needed of the operator A for this kind of approximation technique to work?

In Section 4 we will use the method from this section applied to unitary operators, and use them to extend our approximating results to bounded self-adjoint operators. We leave it to future work to either find a way to extend the method of this section to all bounded normal operators or modify the construction for bounded self-adjoint operators from Section 4 to access bounded normal operators via a decomposition into self-adjoint operators.

3 Spectral measure

In this section we show how weighted counting measures in the finite dimensional spaces give rise to a measure on subsets of $\mathbb {C}$ . With this measure the vector space homomorphism $F^m$ from the previous section becomes an isometric embedding of $L_2(S,\mu )$ into the metric ultraproduct.

For all $N<{\omega }$ , we define a measure $\mu _{N}$ for subsets X of $\mathbb {C}$ : Recall that $\phi =\sum _{k=0}^{D_{N}-1}\xi _{N}(k)u_{N}(k)$ and each $\xi _{N}(k)$ is a non-negative real. We let $\mu _{N}(X)$ be the sum of all $\xi _{N}(k)^{2}$ such that $k<D_{N}$ and $\lambda _{N}(k)\in X$ . Note that, as $\lVert {\phi }\rVert =1$ , $\mu _N(X)\in [0,1]$ for all $N<{\omega }$ and $X\subset \mathbb {C}$ . Then we define $\mu ^{n}(X)$ to be the ultralimit $\lim _{{\mathcal {U}}}\mu _{N}(X)$ of the measures $\mu _{N}(X)$ , i.e., $\mu ^{n}(X)$ is the unique real r such that for all $\varepsilon>0$ , the set

$$ \begin{align*}\{ N<{\omega}\vert\ \vert \mu_{N}(X)-r\vert <\varepsilon\}\in {\mathcal{U}}.\end{align*} $$

We think of $\mu ^n$ as a sort of naive measure, as it is our main tool towards building a measure, but it is defined on all subsets of $\mathbb {C}$ and we have no reason to believe it actually would be a measure. However, we can use it to build a Borel measure.

Definition 3.1. For all reals $r\in [{-}M,M]$ we define lines $I_{r}=\{\lambda \in S\vert \ Re(\lambda )=r\}$ and $J_{r}=\{\lambda \in S\vert \ Im(\lambda )=r\}$ . For all $\varepsilon>0$ we let $I_{r}^{\varepsilon }=\{\lambda \in S\vert \ \vert Re(\lambda )-r\vert <\varepsilon \}$ and $J_{r}^{\varepsilon }=\{\lambda \in S\vert \ \vert Im(\lambda )-r\vert <\varepsilon \}$ . For a point $\lambda \in S$ and $\varepsilon>0$ , we let $\lambda ^{\varepsilon }=\{ x\in S\vert \ \vert Re(\lambda )-Re(x)\vert ,\vert Im(\lambda )-Im(x)\vert <\varepsilon \}$ . We say that a real $r\in [{-}M,M]$ is nice if for all $\delta>0$ there is $\varepsilon>0$ such that $\mu ^{n}(I^{\varepsilon }_{r}),\mu ^{n}(J^{\varepsilon }_{r})<\delta $ .

Lemma 3.2.

1. (i) $\mu ^{n}$ satisfies all the properties of a measure when restricted to finite collections of sets, e.g., if $X\subseteq Y$ , then $\mu ^{n}(X)\le \mu ^{n}(Y)$ and if $X_{i}$ , $i<m$ , are disjoint, then $\mu ^{n}(\cup _{i<m}X_{i})=\sum _{i<m}\mu ^{n}(X_{i})$ .

2. (ii) The set of $r\in [{-}M,M]$ that are not nice is countable. Thus there is a countable dense subset $NI$ of $[{-}M,M]$ such that every $r\in NI$ is nice and ${-}M,M\in NI$ .

Proof. (i): The claim is clear since each $\mu _{N}$ is a measure and thus has these properties.

(ii): Suppose not. Since $-M$ and M are clearly nice, there must be uncountably many reals $r\in [{-}M,M]$ that are not nice. Let these be $r_{i}$ , $i<{\omega }_{1}$ . By symmetry and the pigeon hole principle we may assume that for all $i<{\omega }_{1}$ , the vertical lines witness this. Then by the pigeon hole principle again, we may assume that there is $\delta>0$ such that for all $i<{\omega }_{1}$ and $\varepsilon>0$ , $\mu ^{n}(I^{\varepsilon }_{r_{i}})>\delta $ . Let $K<{\omega }$ be such that $K\delta>1$ . Now for all $i<K$ choose $\varepsilon _{i}>0$ so that the sets $I^{\varepsilon _{i}}_{r_{i}}$ , $i<K$ , are disjoint. But now we can find $N<{\omega }$ such that for all $i<K$ , $\mu _{N}(I^{\varepsilon _{i}}_{r_{i}})>\delta $ . It follows that $\mu _{N}(\cup _{i<K}I^{\varepsilon _{i}}_{r_{i}})>1$ , a contradiction.

Definition 3.3. Let $Sq^{*}$ be the set of all subsets Y such that there are $r_{i}\in NI$ such that

$$ \begin{align*}Y=\{ \lambda\in S\vert\ r_{0}<Re(\lambda )<r_{1},\ r_{2}<Im(\lambda )<r_{3}\} .\end{align*} $$

Now define $\mu ^{*}(Y)$ for any $Y\subseteq Int(S)$ (interior of S) to be the outer measure based on $\mu ^{n}(X)$ , $X\in Sq^{*}$ , i.e.,

$$ \begin{align*}\mu^{*}(Y)=\inf\{\sum_{i=0}^{\infty}\mu^{n}(X_{i})\vert\ X_{i}\in Sq^{*}, Y\subseteq\cup_{i<{\omega}}X_{i}\}.\end{align*} $$

As usual, we say that $X\subseteq Int(S)$ is measurable if for all $Y\subseteq Int(S)$ , $\mu ^{*}(Y)=\mu ^{*}(Y\cap X)+\mu ^{*}(Y-X)$ . For $X\subseteq S$ (or $X\subseteq \mathbb {C}$ ), we let $\mu ^{*}(X)=\mu ^{*}(X\cap Int(S))$ and X is measurable if $X\cap Int(S)$ is. Since there is $\varepsilon>0$ such that for all $N<{\omega }$ and $k<D_{N}$ , $\vert \lambda _{N}(k)\vert <M-\varepsilon $ , it is enough to look at subsets of $Int(S)$ (everything close to the boundary of S has naive measure zero). We write $\overline X$ for the closure of $X\subseteq \mathbb {C}$ .

Lemma 3.4. Let $Y\in Sq^{*}$ .

1. (i) $\mu ^{*}(Y)=\mu ^{*}(\overline Y)=\mu ^{n}(Y)=\mu ^{n}(\overline Y)$ .

2. (ii) Y is measurable.

Proof. (i): Clearly $\mu ^{*}(Y)\le \mu ^{*}(\overline Y)$ . From the choice of $Sq^{*}$ it follows easily that for all $\varepsilon>0$ , there is $X\in Sq^{*}$ such that $\vert \mu ^{n}(X)-\mu ^{n}(Y)\vert <\varepsilon $ and $\overline Y\subseteq X$ . Thus $\mu ^{*}(\overline Y)\le \mu ^{n}(Y)$ and $\mu ^{n}(\overline Y)=\mu ^{n}(Y)$ . Now for a contradiction, suppose that $\mu ^{*}(Y) +\varepsilon <\mu ^{n}(Y)$ for some $\varepsilon>0$ . Then we can find $Y_{i}\in Sq^*$ , $i<{\omega }$ , such that $Y\subseteq \cup _{i<{\omega }}Y_{i}$ and $\sum _{i<{\omega }}\mu ^{n}(Y_{i}) +\varepsilon <\mu ^{n}(Y)$ . But then we can find $X\in Sq^{*}$ such that $\overline X\subseteq Y$ and $\mu ^{n}(Y-\overline X)<\varepsilon $ . Since $\overline X$ is compact, there is $K<{\omega }$ such that $\overline X\subseteq \cup _{i<K}Y_{i}$ . Now

$$ \begin{align*}\mu^{n}(Y- \overline X)+\sum_{i<K}\mu^{n}(Y_{i})<\mu^{n}(Y),\end{align*} $$

a contradiction by Lemma 3.2.

(ii): By the definition of the outer measure $\mu ^*$ , and by considering coverings, it is enough to show that if $X\in Sq^{*}$ , then $\mu ^{*}(X-Y)+\mu ^{*}(X\cap Y)=\mu ^{*}(X)$ . Clearly $\mu ^{*}(X-Y)+\mu ^{*}(X\cap Y)\ge \mu ^{*}(X)$ . On the other hand there are $k\le 4$ and disjoint $Z_{i}\in Sq^{*}$ , $i<k$ , such that $\cup _{i<k}Z_{i}\subseteq X-Y$ and $X-Y\subseteq \cup _{i<k}\overline Z_{i}$ . Notice that $X\cap Y\in Sq^{*}$ . Now

$$ \begin{gather*}\mu^{*}(X-Y)\le\mu^{*}(\cup_{i<k}\overline Z_{i})\le\sum_{i<k}\mu^{*}(\overline Z_{i})=\\[5pt]=\sum_{i<k}\mu^{*}(Z_{i})=\sum_{i<k}\mu^{n}(Z_{i})=(\sum_{i<k}\mu^{n}(Z_{i}))+\mu^{n}(X\cap Y)-\mu^{n}(X\cap Y)\le\\[5pt]\le\mu^{n}((X\cap Y)\cup\cup_{i<k}Z_{i})-\mu^{n}(X\cap Y)\le\mu^{n}(X)-\mu^{n}(X\cap Y)=\mu^{*}(X)-\mu^{*}(X\cap Y).\end{gather*} $$

Now as usual one can see that the collection of measurable sets is closed under countable unions and complements. In particular every Borel set ( $\subseteq S$ ) is measurable. For measurable X ( $\subseteq S$ ), we write $\mu (X)=\mu ^{*}(X)$ and then $\mu $ is a Borel measure on S. Notice that by Lemma 3.4, $\mu (S)=\mu ^{*}(S)=\mu ^{n}(S)=1$ (recall Equation (7) and that $\phi $ has norm $1$ ).

When working with the measure and later for constructing rigged Hilbert spaces, it will be convenient to have a sequence of refinements in $Sq^*$ .

Definition 3.5. Let, for each $k<\omega $ , $Sq_{k}\subseteq Sq^{*}$ be a finite set so that:

1. (a) the elements of $Sq_{k}$ are disjoint,

2. (b) $\cup _{X\in Sq_{k}}\overline X =S$ ,

3. (c) for all $X\in Sq^{*}$ and $m<{\omega }$ , there are $m<k<{\omega }$ and $Z\subseteq Sq_{k}$ such that $\overline X=\cup _{Y\in Z}\overline Y$ ,

4. (d) if $k<l<{\omega }$ , $X\in Sq_{k}$ , then there is $Z\subseteq Sq_{l}$ such that $\overline X =\cup _{Y\in Z}\overline Y$ , and

5. (e) if $Y=\{ \lambda \in S\vert \ r_{0}<Re(\lambda )<r_{1},\ r_{2}<Im(\lambda )<r_{3}\}\in Sq_{k}$ , then $r_{0}<r_{1}$ , $r_{1}-r_{0}<2M/(k+1)$ , $r_{2}<r_{3}$ and $r_{3}-r_{2}<2M/(k+1)$ .

We let $Sq=\cup _{k<{\omega }}Sq_{k}$ .

Remark 3.6. Now by Lemma 3.4, it is easy to see that for all $X\subseteq S$ ,

$$ \begin{align*}\mu^{*}(X)=\inf\{\sum_{i=0}^{\infty}\mu^{n}(X_{i})\vert\ X_{i}\in Sq, X\subseteq\cup_{i<{\omega}}\overline X_{i}\} .\end{align*} $$

We will use this frequently without mentioning it.

Now $L_{2}(S,\mu )$ is a Hilbert space and we write $\Vert \cdot \Vert _{2}$ also for the norm of this space. Elements of $L_{2}(S,\mu )$ are equivalence classes of the equivalence relation $\Vert f-g\Vert _{2}=0$ and we write $[f]_{2}$ for these equivalence classes. Then as usual we write $C(S)$ also for $\{ [f]_{2}\vert \ f\in C(S)\}$ and similarly for $D(S)$ . For each equivalence class $x\in C(S)$ we fix a continuous $f_{x}:S\rightarrow \mathbb {C}$ so that $x=[f_{x}]_{2}$ . We will see later (in Lemma 3.12) that this determines $f_{x}$ on $\sigma (A)$ and what $f_x$ does outside $\sigma (A)$ doesn’t matter. Now later when a function gives a value in $C(S)$ which is an equivalence class, we can think of it also as a continuous function from S to $\mathbb {C}$ . Thus $L_{2}(S,\mu )$ and $L_{2}(\sigma (A),\mu \restriction \sigma (A))$ are naturally isomorphic since every $f\in C(\sigma (A))$ extends to a (bounded uniformly) continuous function $f'\in C(S)$ .

Our next step is to show that the mappings $F^m:D(S)\to H^m$ and $G:D(S)\to H$ are not only vector space homomorphisms, but also isometries under the $L_2$ norm, which will let us define $F^m([f]_{2})=F^m(f)$ and $G([f]_{2})=G(f)$ to get isometric embeddings of $L_2(S,\mu )$ into $H^m$ and H respectively.

Lemma 3.7. For all $P\in \mathbb {C} [X,Y]$ , $\Vert F^u(f_{P})\Vert _{2}=\Vert f_{P}\Vert _{2}$ .

Proof. This proof is essentially the same as the proof that shows that continuous functions are Riemann integrable. Let $1>\varepsilon >0$ , $m=1+ \sup \{\vert f_{P}(\lambda )\vert \ \vert \ \lambda \in S\}$ and choose $k>0$ so that if $\vert \lambda -\lambda '\vert <4M/k$ (which happens for all $\lambda ,\lambda '\in \overline Y$ , for $Y\in Sq_k$ ), then $\vert f_{P}(\lambda )-f_{P}(\lambda ')\vert <\varepsilon /8m$ . Then we can choose $W\in {\mathcal {U}}$ such that for all $N\in W$ and $Y\in Sq_{k}$ , both $\vert \mu (Y)-\mu _{N}(Y)\vert $ and $\vert \mu (\overline Y)-\mu _{N}(\overline Y)\vert $ are $ {<\varepsilon /(4m^{2}\vert Sq_{k}\vert )}$ . Notice that if we let X be the union of all $\overline Y-Y$ , $Y\in Sq_{k}$ , then $\mu (X)=0$ , and

$$ \begin{align*}\lVert{\sum_{\lambda_{N}(k)\in X}\xi_{N}(k)f_{P}(\lambda_{N}(k))u_{N}(k)}\rVert_2^2\leq\mu_N(X)m^2<\varepsilon/4.\end{align*} $$

Then

$$ \begin{align*} \vert\ (\Vert F_{N}(f_{P})\Vert_{2})^{2}-(\Vert f_{P}\Vert_{2})^{2}\ \vert =\vert\ \sum_{k<D_N}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_S\lvert{f_P(x)}\rvert^2d\mu \ \vert\\ =\vert\ \sum_{\lambda_N(k)\in X}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 +\sum_{Y\in Sq_k}\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2\\ - \sum_{Y\in Sq_k}\int_Y\lvert{f_P(x)}\rvert^2d\mu \ \vert\qquad\ \quad\qquad\\ \leq \varepsilon/4 +\sum_{Y\in Sq_k}\lvert{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_Y\lvert{f_P(x)}\rvert^2d\mu}\rvert, \end{align*} $$

and for each $Y\in Sq_k$

$$ \begin{align*} \lvert{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(\lambda_N(k))}\rvert^2 - \int_Y\lvert{f_P(x)}\rvert^2d\mu}\rvert\qquad\qquad\qquad\\ \leq \int_Y \left(\frac{\sum_{l_N(k)\in Y}\xi_N(k)^2\lvert{\lvert{f_P(\lambda_N(k))}\rvert^2-\lvert{f_P(x)}\rvert^2}\rvert}{\mu(Y)}\right.\\ \left.\quad +\lvert{\frac{\sum_{\lambda_N(k)\in Y}\xi_N(k)^2\lvert{f_P(x)}\rvert^2}{\mu(Y)}-\lvert{f_P(x)}\rvert^2}\rvert\right)d\mu\\ \leq \int_Y \left(\frac{\mu_N(Y)2m\frac{\varepsilon}{8m}}{\mu(Y)}+\lvert{\frac{\mu_N(Y)}{\mu(Y)}-1}\rvert m^2\right)d\mu\\ =\mu_N(Y)\frac{\varepsilon}{4}+\lvert{\mu_N(Y)-\mu(Y)}\rvert m^2\\ < \mu_N(Y)\frac{\varepsilon}{4}+\frac{\varepsilon}{4\lvert{Sq_k}\rvert}. \end{align*} $$

Putting this together (and recalling $\mu _N(S)=1$ ), we get

$$ \begin{align*}\vert\ (\Vert F_{N}(f_{P})\Vert_{2})^{2}-(\Vert f_{P}\Vert_{2})^{2}\ \vert \le\varepsilon/4 +\varepsilon /4 +\varepsilon/4<\varepsilon \end{align*} $$

from which the claim follows.

Corollary 3.8. $F^m([f]_{2})=F^m(f)$ and $G([f]_{2})=G(f)$ are isometric embeddings of $L_2(S,\mu )$ into $H^m$ and H respectively.

Proof. By the lemma above, and noting that $G=(G^{m})^{-1}F^m$ (see Corollary 2.7), we see that $F^m$ and G are well-defined on the $\lVert {\cdot }\rVert _2$ equivalence classes of $D(S)$ . Now we notice that $\mathbb {C} [X,Y]$ is closed under the function $f\mapsto f^{*}$ , where $f^{*}(\lambda )=\overline {f(\lambda )}$ . And thus by Stone–Weierstrass, $D(S)$ is dense in $C(S)$ even in the uniform convergence topology (we will need this later). And since $C(S)$ is dense in $L_{2}(S,\mu )$ , see, e.g., [2, Corollary 4.2.2], $D(S)$ is dense in $L_{2}(S,\mu )$ . Thus we can extend the functions $F^m$ and G to all of $L_{2}(S,\mu )$ by continuity.

Remark 3.9. Recall that on $D(S)$ , we have $A_D(f_P)(\lambda )=\lambda f_P(\lambda )$ and $A^*_D(f_P)(\lambda )=\overline \lambda f_P(\lambda )$ . These can also be defined on the $\lVert {\cdot }\rVert _2$ equivalence classes by $A_{D}([f]_{2})=[A_{D}(f)]_{2}$ (and similarly for $A^{*}_{D}$ ), and then extend it to all of $L_2(S,\mu )$ by continuity.

Corollary 3.10. $F^m$ is an isometric isomorphism from $L_{2}(S,\mu )$ to $H^{Im}$ and ${A^{m}\restriction H^{Im}=F^mA_{D}(F^m)^{-1}}$ . Thus also $G=(G^{m})^{-1}F^m$ is an isometric isomorphism from $L_{2}(S,\mu )$ to H and $A=GA_{D}G^{-1}$ .

We have been looking at $L_2(S,\mu )$ , where S was chosen to be a ‘big enough’ set. However, $\mu $ only puts weight on part of this set, and next we will show that set is exactly the spectrum of A. As pointed out above, there is a rational number ${0<q<M}$ such that for all $N<{\omega }$ , the norm of $A_{N}$ is $<q$ since the norm of $A_{N}$ is at most the norm of A. Thus if we let $S^{-}=\{\lambda \in \mathbb {C}\vert \ -M< Re(\lambda )<M, -M< Im(\lambda )<M\}$ then $\mu (S^{-})=\mu (S)=1$ .

Definition 3.11. Let $\sigma (A)$ be the set of all $\lambda \in \mathbb {C}$ such that $A-\lambda I$ does not have a bounded inverse. Notice that $\lambda \in \sigma (A)$ iff for all $\varepsilon>0$ , there is $\psi \in H$ such that $\Vert \psi \Vert _{2}=1$ and $\Vert A(\psi )-\lambda \psi \Vert _{2}<\varepsilon $ . We let $\tilde {\sigma }(A)$ be the set of all $\lambda \in S^{-}$ such that every open neighborhood of $\lambda $ that is contained in $S^{-}$ has measure $>0$ .

Lemma 3.12. $\sigma (A)=\tilde {\sigma }(A)$ .

Proof. By Corollary 3.10, it is enough to show that $\sigma (A_{D})=\tilde {\sigma }(A)$ , where $\sigma (A_{D})$ is defined as $\sigma (A)$ was. Also if $\lambda \not \in S^{-}$ , $\lambda $ does not belong to either of the sets. So suppose that $\lambda \in S^{-}$ .

We write $B_{r}(\lambda )$ , r a positive real number, for the set of all $\lambda '\in \mathbb {C}$ such that $\vert \lambda -\lambda '\vert <r$ . Now if for some r, $B_{r}(\lambda )\subseteq S^{-}$ and $\mu (B_{r}(\lambda ))=0$ , then it is easy to see that $\Vert A_{D}(f)-\lambda f\Vert _{2}\ge r$ for all f with norm $1$ and thus $\lambda \not \in \sigma (A_{D})$ . On the other hand, if for all positive r such that $B_{r}(\lambda )\subseteq S^{-}$ , $\mu (B_{r}(\lambda ))>0$ , then for all such r, we can find $f\in C(S )$ such that $\Vert f\Vert _{2}=1$ and $f(x)=0$ for all $x\in S-B_{r}(\lambda )$ . Then $\Vert A_{D}(f)-\lambda f\Vert _{2}<r$ . Thus $\lambda \in \sigma (A_{D})$ .

Corollary 3.13. $\mu (\sigma (A))=1$ and $\mu (S-\sigma (A))=0$ .

Proof. $\sigma (A)=\tilde {\sigma }(A)$ is a closed set and thus measurable and thus the claims follow from Lemma 3.12 and $\mu (S)=\mu (S^-)=1$ .

Looking back at the constructions of this and the past section, one notes that the finite dimensional spaces $H_N$ depend on the choice of $\phi $ , and thus it is likely that one gets different $H^u$ and $H^m$ depending on the choice of cyclic vector. We have not looked into this, as the whole of these spaces are too big for our interest. As every $H_N$ has a part, where the operator is replaced by a wraparound-mapping, these erroneous parts will show up in the ultraproduct, and we are really interested only in parts stemming from the original operator. There are subspaces where these errors disappear, and one of them is $H^{Im}$ , which is canonical, as we have showed it to be isometrically isomorphic to H. A natural question arises:

Open question 3. Is there a natural characterization for the subspaces $H^m$ where the errors of the $A_N$ ’s disappear?

As for the canonicity of our measure $\mu $ we have the following:

Corollary 3.14. The measure $\mu $ constructed is independent of the choice of cyclic vector. In particular all measures constructed in the above manner will agree on measure zero sets, and thus agree on which reals are nice.

Proof. This follows from Corollary 3.10 and the uniqueness of the spectral measure (see, e.g., Section VII.2 of [9]).

However, note that in general $\sigma (A)\neq \sigma (A^m)$ , as the latter can be strictly larger. Thus we are not considering elementary embeddings into the (metric) ultraproduct, but only embeddings. This is enough for our purposes, as we only use the construction for calculating equations.

4 Self-adjoint operators

In this section we show that the constructions from Sections 2 and 3 can be generalized to (bounded) self adjoint operators.

We will need the following facts, some of which seem hard to find in the literature (in particular item (iv) of the fact). Our version is not the best possible.

Fact 4.1. Let H be a separable Hilbert space and B a self-adjoint, U a unitary operator on H and I the identity operator.

1. (i) $\max \{\vert \lambda \vert \,\vert \, \lambda \in \sigma (B)\}=\Vert B\Vert $ , $e^{iB}$ is unitary and $\sigma (e^{iB})=\{e^{i\lambda } \vert \lambda \in \sigma (B)\}$ .

2. (ii) Let r and q be reals. $e^{i(B+r I)}=e^{iB}\circ e^{ir}I$ , $e^{iq}\in \sigma (e^{iB})$ iff $e^{i(q +r)}\in \sigma (e^{i(B+r I)})$ and $\lambda \in \sigma (B)$ iff $\lambda +r\in \sigma (B+rI)$ .

3. (iii) Suppose $H_{0}$ is a complete subspace of H, $H_{1}$ its orthogonal complement and $A_{i}$ are bounded operators on $H_{i}$ , $i<2$ . Then there is a unique operator A on H such that $A\restriction H_{i}=A_{i}$ for both $i<2$ and it is bounded and $\sigma (A)=\sigma (A_{0})\cup \sigma (A_{1})$ . If in addition both operators $A_{i}$ are self-adjoint, then also A is self-adjoint and if both are unitary, then also A is unitary.

4. (iv) If $0\le r<\pi /2$ and for all $\lambda \in \sigma (U)$ , $\lambda =e^{iq}$ for some $q\in [{-}r,r]$ , then there is a unique self-adjoint operator A such that $U=e^{i A}$ and $\sigma (A)\subseteq [{-}r,r]$ .

Proof. (i): The first claim is the spectral radius formula (for a proof see, e.g., Chapter VI of [9]) the others are proved via polynomial approximations, see Chapter VII of [9].

(ii): The first claim follows from the fact that B and $r I$ commute. The rest is easy.

(iii): Obviously A must be such that if $v\in H_{0}$ and $u\in H_{1}$ , then $A(v+u)=A_{0}(v)+A_{1}(u)$ and this is a bounded operator. Also clearly $\sigma (A_{0})\cup \sigma (A_{1})\subseteq \sigma (A)$ and since spectra are closed the other direction follows by an easy calculation. If $A_{0}$ and $A_{1}$ are self adjoint, then for all $v_{0},v_{1}\in H_{0}$ and $u_{0},u_{1}\in H_{1}$ ,

$$ \begin{align*}\langle A(v_{0}+v_{1})|u_{0}+u_{1}\rangle=\langle A_{0}(v_{0})|u_{0}\rangle+\langle A_{1}(v_{1})|u_{1}\rangle=\end{align*} $$

$$ \begin{align*}=\langle v_{0}|A_{0}(u_{0})\rangle+\langle v_{1}|A_{1}(u_{1})\rangle=\langle v_{0}+v_{1}|A(u_{0}+u_{1})\rangle,\end{align*} $$

where the first and the third identity follow from the choice of $H_{0}$ and $H_{1}$ . Finally if $A_{0}$ and $A_{1}$ are unitary, easy calculations show that A is norm preserving and onto.

(iv): Let $U'=e^{i\pi }U$ . Then $U'$ is unitary, and if $\lambda \in \sigma (U')$ , then $\lambda =e^{iq}$ for some $q\in [{-}r+\pi ,r+\pi ]$ . Now by [11, Theorem 8.4], there is a unique self-adjoint operator $A'$ such that $U'=e^{i2\pi A'}$ and the spectrum of $A'$ is a subset of $[0,1]$ and 0 is not in the point spectrum of $A'$ . By item (i), the spectrum of $2\pi A'$ is a subset of $[\pi -r,\pi +r]$ . Let $A=2\pi A'-\pi I$ . Then $e^{iA}=U$ , $\sigma (A)\subseteq [{-}r,r]$ and the uniqueness follows from the uniqueness of $A'$ and (ii).

From now on, in this section we assume that $Re(e^{i})\in NI$ . If this is not true, we can replace $1$ by a real q close to $1$ such that $Re(e^{iq})\in NI$ and work with it.

Let B be a bounded self-adjoint operator on a separable Hilbert space H. It will turn out that it does not matter whether we look at B or $rB$ for some positive real r, and thus we may assume that the norm of B is $\leq 1$ . Also we may assume that $B(v)\ne 0$ for all $v\in H-\{ 0\}$ because we can always restrict B to the orthogonal complement of its kernel (which is closed under B since B is self-adjoint). Let $A=e^{iB}$ . Then A is unitary and not the identity by Fact 4.1. Also by the same fact, if $\lambda \in \sigma (A)$ , then $\lambda =e^{iq}$ for some $q\in [-1,1]$ .

In the proof of the following lemma, the assumption that the norm of B is small plays an important role, stemming from Fact 4.1. We will need the uniqueness of the self-adjoint operator in point (iv) of the fact, and for that we need to avoid a ‘wraparound’. Our formulation of the fact allows for B to have norm smaller that $\pi /2$ , and we have chosen 1 as it is convenient in calculations.

Lemma 4.2. If $H_{0}$ is a complete subspace of H and closed under A and $A^{*}$ , then it is closed under B.

Proof. Suppose not. Let $H_{1}$ be the orthogonal complement of $H_{0}$ in H. Then $H_{1}$ is closed under A and $A^{*}$ and there are self-adjoint operators $B_{0}$ in $H_{0}$ and $B_{1}$ in $H_{1}$ such that $e^{i B_{0}}=A\restriction H_{0}$ and $e^{i B_{1}}=A\restriction H_{1}$ . But then by Fact 4.1(iii) there is a self-adjoint operator $B'$ in H such that $e^{i B'}=A$ (because $e^{i B'}\restriction H_{0}=A\restriction H_{0}$ and $e^{i B'}\restriction H_{1}=A\restriction H_{1}$ and A is uniquely determined by $A\restriction H_0$ and $A\restriction H_1$ ) and $B'\ne B$ . This contradicts Fact 4.1(iii).

By Lemma 4.2, if we may assume that H has a cyclic vector with respect to the operator A as in Section 2, we have spaces $H_{N}$ , operators $A_{N}$ , functions G, $G^{m}$ , $F^m$ and $F_{N}$ , a spectral measure $\mu $ etc. as in sections 2 and 3. Notice that each $A_{N}$ is a unitary operator and thus for all $N<{\omega }$ and $n< D_{N}$ , $\lambda _{N}(n)=e^{iq}$ for some $q\in ]-\pi ,\pi ]$ . It follows that $\mu (S-S_{0})=0$ when $S_{0}$ is the set $\{ e^{iq}\vert \ q\in ]-\pi ,\pi ]\}$ .

We define operators $B_{N}$ as follows: $B_{N}(u_{N}(n))=qu_{N}(n)$ if $A_{N}(u_{N}(n))=e^{iq}u_{N}(n)$ and $q\in ]-\pi ,\pi ]$ . We write $B^{m}$ for the metric ultraproduct (with the filter ${\mathcal {U}}$ as in the previous sections) of the operators $B_{N}$ . Then $A_{N}=e^{iB_{N}}$ for all $N<{\omega }$ and since the operators $B_{N}$ are uniformly bounded (by $\pi $ ) it is easy to see that $A^{m}=e^{iB^{m}}$ . Also each $B_{N}$ is self-adjoint and thus also $B^{m}$ is self-adjoint. We want to show the following:

Theorem 4.3. $B^{m}\restriction H^{Im}=G^{m}B(G^{m})^{-1}$ .

This follows immediately from Fact 4.1(iv) if we know that $H^{Im}$ is closed under $B^{m}$ . So what we need to show is the following:

Lemma 4.4. $H^{Im}$ is closed under $B^{m}$ .

Proof. Suppose not. Note that from Corollaries 2.7 and 3.8 it follows that $H^{Im}:=rng(G^m)=rng(F^m)$ . Let $H_{0}$ be the closure of $H^{Im}$ under $B^{m}$ i.e., the complete subspace of $H^{m}$ generated by the set

$$ \begin{align*}\{ (B^{m})^{k}(F^m(f_{P}))\vert\ P\in \mathbb{C}[X,Y],\ k<{\omega}\}\end{align*} $$

(keep in mind that $B^{m}$ is bounded). Then $H^m$ is a complete subspace of $H_0$ , closed under $A^m$ and $A^{m*}$ , so we get a contradiction as in the proof of Lemma 4.2, unless the norm is too large to guarantee uniqueness. But this we can rule out by showing the following:

Claim 4.4.1. The operator norm of $B^{m}\restriction H_{0}$ is $\le 1$ .

Proof. For a contradiction suppose that there is $\varepsilon>0$ , $k<{\omega }$ and $P\in \mathbb {C} [X,Y]$ such that $\Vert B^{m}((B^{m})^{k}(F^m(f_{P})))\Vert>(1+\varepsilon )\Vert (B^{m})^{k}(F^m(f_{P}))\Vert $ . Since A is not the identity, $\mu (\{ 1\} )<1$ . So there are $\delta>0$ and $V\subseteq \sigma (A)$ such that $\mu (V)>\delta $ , for all $\lambda \in V$ , $\vert f_{P}(\lambda )\vert>\delta $ and if $\lambda =e^{iq}\in V$ , then $\vert q\vert>\delta $ .

For all $N<{\omega }$ , let $H^{0}_{N}$ be the subspace of $H_{N}$ generated by those $u_{N}(n)$ for which $\lambda _{N}(n)=e^{iq}$ for some $q\in [-\pi ,\pi ]$ such that $\vert q\vert>1$ and let $H^{1}_{N}$ be the subspace of $H_{N}$ generated by those $u_{N}(n)$ for which $\lambda _{N}(n)=e^{iq}$ for some $q\in [-\pi ,\pi ]$ such that $\vert q\vert \le 1$ . Then $H^{1}_{N}$ is the orthogonal complement of $H^{0}_{N}$ . Further let $H^2_N$ be the subspace of $H_N$ generated by those $u_N(n)$ for which $\lambda _N(n)\in V$ . Let $v_{i}(N)$ be the projection of $F_{N}(f_{P})$ to $H^{i}_{N}$ , $i<3$ . Let $S^{*}$ be the set of all $\lambda \in S$ such that $Re(\lambda )\ge Re(e^{i})$ . Notice that since $Re(e^{i})\in NI$ (see the assumption immediately after the proof of Fact 4.1), $\mu (S^{*})$ and $\mu (S-S^{*})$ are ultralimits of $\mu _{N}(S^{*})$ and $\mu _{N}(S-S^{*})$ . Let s be the supremum of all $\vert f_{P}(\lambda )\vert $ for $\lambda \in S$ .

Now

1. (a)

   $$ \begin{align*}&\lVert {(B_N)^k(F_N(f_P))}\rVert \geq \lVert {(B_N)^k(v_2(N))}\rVert =\\&\quad =\lVert{(B_N)^k\sum_{\lambda_N(n)\in V}\xi_N(n)f_P(\lambda_N(n))u_N(n)}\rVert\geq \delta^{k+3/2}\end{align*} $$
   in a set of N’s that belongs to ${\mathcal {U}}$ ,

2. (b)

   $$ \begin{align*}&\lVert {B_N((B_N)^k(F_N(f_P)))}\rVert =\lVert {(B_N)^{k+1}(v_0(N)+v_1(N))}\rVert \leq\\&\quad\pi^{k+1}\sqrt{\mu_N(S-S^*)}s+\lVert{v_1(N)}\rVert\end{align*} $$
   in a set of N’s that belongs to ${\mathcal {U}}$ ,

3. (c) $\mu _{N}(S-S^{*})\le (\varepsilon \delta ^{k+3/2}/(2\pi ^{k+1}s))^{2}$ in a set of N’s that belong to ${\mathcal {U}}$ (since $\mu (S-S^{*})=0$ by the assumption $\lVert {B}\rVert \leq 1$ and the construction of the measure for A).

By putting these together, we get

$$ \begin{align*}\lVert{B_N((B_N)^k(F_N(f_P)))}\rVert\leq \pi^{k+1}\sqrt{\mu_N(S-S^*)}s+\lVert{v_1(N)}\rVert\leq (\frac{\varepsilon}{2}+1)\lVert{(B_N)^k(F_N(f_P))}\rVert \end{align*} $$

in a set of N’s that belongs to ${\mathcal {U}}$ , which is a contradiction.

Now we can define an operator $B_{D}$ on $L_{2}(S,\mu )$ the natural way: For $f\in C(S)$ , we let $B_{D}(f)(\lambda )=K_B(\lambda )f(\lambda )$ , where $K_B(\lambda )=q$ if $q\in ]-\pi ,\pi ]$ and $\lambda =pe^{iq}$ for some real number p. Now it is easy to see that $e^{iB_{D}}=A_{D}$ and thus by Fact 4.1, $B^{m}\restriction H^{Im}=F^m B_{D}(F^m)^{-1}$ .

If we want for B exactly the same setup as for A we can do the following: Let ${S_{B}=]-\pi ,\pi ]}$ and define a Borel measure $\mu _{B}$ on $S_{B}$ by letting $\mu _{B}(X)=\mu (K_{B}^{-1}(X))$ . Then we can define an operator $B^{\prime }_{D}$ on $L_{2}(S_{B},\mu _{B})$ so that for all $f\in C(S_{B})$ , $B^{\prime }_{D}(f)(q)=qf(q)$ . Finally we notice that if we define a continuous $F_{B}: L_{2}(S,\mu )\rightarrow L_{2}(S_{B},\mu _{B})$ so that for $f\in C(S)$ , $F_{B}(f)(q)=f(e^{iq})$ we get an isometric isomorphism and $B^{\prime }_{D}=F_{B}B_{D}F_{B}^{-1}$ .

5 Rigged Hilbert spaces

Rigged Hilbert spaces are a way of accounting for objects that don’t fit into a Hilbert space, such as Dirac delta functions. A rigged Hilbert space consists of a Hilbert space H and a subspace $\Phi $ (with a finer norm topology than the one given by the norm in H). One then has

$$ \begin{align*}\Phi\subset H\subset \Phi^*, \end{align*} $$

where $\Phi ^*$ is the dual space of $\Phi $ . The elements in $\Phi ^*$ are antilinear functionals, and if $\Phi $ was suitably chosen with respect to a cyclic, essentially self adjoint operator B, then the functionals act as generalized eigenvectors corresponding to values in the spectrum of B (see, e.g., [8]).

In this section we set out to find something similar to $\Phi ^*$ by considering different norms in our ultraproduct space $H^u$ , and finding extensions of $H^{Im}$ . Here, as well as in the next section, it does not matter whether we look at a self-adjoint bounded B or $e^{iB}$ , and thus we return to the assumptions of sections 2 and 3, i.e., that A is bounded, $A\circ A^{*}=A^{*}\circ A=r_{A}I$ and $\phi $ is a cyclic vector. Also we let $H_{N}$ , $A_{N}$ etc. be as in these sections.

We will look at two norms, that end up being essentially an $L_{\infty }$ -norm and an $L_{1}$ -norm. The latter of these will be called $\Vert \cdot \Vert _{0}$ in order to avoid confusion. Strictly speaking both of these may be only seminorms in the finite dimensional spaces $H_{N}$ , but we will call them norms for simplicity. In the ultraproduct we will fraction out all vectors to which the seminorm gives an infinitesimal value, and then the seminorms become norms, and we obtain spaces $H^m_0$ and $H^m_\infty $ somewhat similarly to how we obtained $H^m$ for the $\lVert {\cdot }\rVert _2$ -norm before. Then we will show how generalized distributions embed into $H^m_0$ such that values of the distribution can be calculated via a pairing function resembling an inner product.

Definition 5.1. Consider the following functions from $H_{N}$ to $\mathbb {C}$ : Let $X\subseteq \mathbb {C}$ be a closed set such that $X\subseteq S$ . Then

$$ \begin{align*}\Vert\sum_{n=0}^{D_{N}-1}a_{n}u_N(n)\Vert^{X}_{\infty}=\sup\{\xi_{N}(n)^{-1}\vert a_{n}\vert\ \vert\ \lambda_{N}(n)\in X\} ,\end{align*} $$

where by $0^{-1}$ we mean $0$ , and

$$ \begin{align*}\Vert\sum_{n=0}^{D_{N}-1}a_{n}u_N(n)\Vert_{0}=\sum_{n=0}^{D_{N}-1}\xi_{N}(n)\vert a_{n}\vert .\end{align*} $$

Keep in mind that for all N and n, $\xi _{N}(n)$ is a non-negative real number $\le 1$ .

We define the $\lVert {\cdot }\rVert ^X_\infty $ -norm this way to get something that corresponds to an $L_\infty $ -norm. When the map $F_N$ maps functions over S into vectors in $H_N$ , it carries with it a weight factor that needs to be removed in order to achieve this. And disregarding the values where $\xi _N(n)=0$ corresponds to disregarding values in a set of measure 0.

When constructing $H^m$ from the $\lVert {\cdot }\rVert _2$ -norm we just fractioned out infinitesimals and discarded elements of infinite length. For our other norms we need to be a bit more careful. We start with $\Vert \cdot \Vert _{0}$ . As with the Hilbert space norm, this gives first a function from $H^{u}$ to $\mathbb {C}^{u}$ , denoted by $\Vert \cdot \Vert ^{u}_{0}$ . Note that the function is always defined, with values in a real closed field, but for some vectors the value may be $>n$ for all natural numbers n. Further we get an equivalence relation on $H^u$ by $v\sim _0w$ iff $\lVert {v-w}\rVert ^u_0$ is infinitesimal.

Definition 5.2. Let $n<{\omega }$ , $Y\subseteq Sq_{n}$ , $R^{Y}_{0}=\cup _{R\in Y}R$ , $S^{Y}_{0}=\cup _{R\in Y}\overline R$ , $R^{Y}_{1}=\cup _{R\in Sq_{n}-Y}R$ and $S^{Y}_{1}=\cup _{R\in Sq_{n}-Y}\overline R$ . We say that Y is good if the distance between $\sigma (A)$ and $S^{Y}_{1}$ is $>0$ (then $\sigma (A)\subseteq S^{Y}_{0}$ ). We say that

$$ \begin{align*}(\sum_{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega}}/{\mathcal{U}}\in H^{u}\end{align*} $$

(and $(\sum _{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega }}$ ) is $0$ -good if for all good Y

$$ \begin{align*}(\sum_{\lambda_{N}(k)\in S^{Y}_{1}}\xi_{N}(k)\vert a^{N}_{k}\vert )_{N<{\omega}}/{\mathcal{U}}/\sim =0.\end{align*} $$

Then we let $H^{m0}$ be the set of all $0$ -good $f/{\mathcal {U}}\in H^{u}$ such that $\Vert f/{\mathcal {U}}\Vert ^{u}_{0}<n$ for some natural number n. And we let $H^{m}_{0}=H^{m0}/\sim _{0}$ . Finally, we define the norm $\Vert \cdot \Vert _{0}$ on $H^{m}_{0}$ as before: $\Vert f/{\mathcal {U}}/\sim _{0}\Vert _{0}=q$ if $q\in \mathbb {C}$ is the unique element such that for all $\varepsilon>0$ ,

$$ \begin{align*}\{ N<{\omega}\vert\ \vert\Vert f(N)\Vert_{0}-q\vert <\varepsilon\}\in {\mathcal{U}}.\end{align*} $$

With this norm $H^{m}_{0}$ is a Banach space (addition and scalar multiplication are defined as before). In order to simplify the notation, for all $f\in \Pi _{N\in {\omega }}H_{N}$ , we write $[f]_{0}=f/{\mathcal {U}}/\sim _{0}$ . Notice that if $f,g\in H^{u}$ and $\Vert f-g\Vert ^{u}_{0}$ is infinitesimal and f is $0$ -good, then so is g. We also have the following:

Lemma 5.3. For all $f\in C(S)$ , $F^u(f)\in H^{m0}$ and $\Vert f\Vert _{1}=\Vert [F^u(f)]_{0}\Vert _{0}$ .

Proof. For the first claim, note that $\mu (S)$ is bounded and, for a good Y, $\mu ^n(S^Y_1)=\mu (S^Y_1)=0$ , so as f is bounded, $F^u(f)$ is 0-good and has bounded $\lVert {\cdot }\rVert ^u_0$ -norm.

For the second claim, note that f is uniformly continuous and thus Riemann integrable, so we can for each $l<{\omega }$ and $X\in Sq_l$ pick any element $c_X\in X$ and then

$$ \begin{align*}\lVert{f}\rVert_1=\lim_{l\to\infty}\sum_{X\in Sq_l}\mu(X)\lvert{f(c_X)}\rvert. \end{align*} $$

On the other hand,

$$ \begin{align*}\lVert{F^u(f)}\rVert^u_0=\lim_{N,{\mathcal{U}}}\sum_{k<D_N}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert =\lim_{N,{\mathcal{U}}}\sum_{X\in Sq_l}\sum_{k<D_N,\lambda_N(k)\in X}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert \end{align*} $$

for any l, and if l is large enough so that values of f differ only slightly within each $X\in Sq_l$ , we can replace all the eigenvalues within X with the $c_X$ from above and have

$$ \begin{align*}\sum_{X\in Sq_l}\sum_{k<D_N,\lambda_N(k)\in X}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert\approx \sum_{X\in Sq_l}\mu_N(X)\lvert{f(c_X)}\rvert. \end{align*} $$

For any l, we also have that for $X\in Sq_l$ , $\mu (X)=\mu ^n(X)=\lim _{N,{\mathcal {U}}}\mu _N(X)$ .

So for any $\varepsilon>0$ , we can choose an l large enough to get (for all N).

$$ \begin{align*}\lvert{\sum_{k<D_N}\xi_N(k)^2\lvert{f(\lambda_N(k))}\rvert-\sum_{X\in Sq_l}\mu_N(X)\lvert{f(c_X)}\rvert}\rvert<\varepsilon.\\[-45pt] \end{align*} $$

Let us then look at the norm $\Vert \cdot \Vert _{\infty }$ First we will need a modified version of the $\sup $ -norm on $C(S)$ :

Definition 5.4. We define a seminorm $\Vert f\Vert ^\sigma _{\infty }=\sup \{\vert f(\lambda )\vert \ \vert \ \lambda \in \sigma (A)\}$ on $C(S)$ and write $L_{\infty }(S,\mu )$ for $C(S)/\sim ^\sigma _{\infty }$ , where $f\sim ^\sigma _{\infty }g$ if $\Vert f-g\Vert ^\sigma _{\infty }=0$ .

Then $\Vert \cdot \Vert ^\sigma _{\infty }$ is a norm on $L_{\infty }(S,\mu )$ .

Definition 5.5. For all $\varepsilon>0$ , we let $X_{\varepsilon }$ be the set of all $\lambda \in \mathbb {C}$ whose distance to $\sigma (A)$ is $\le \varepsilon $ and we let $\Vert (v_{N})_{N<{\omega }}/{\mathcal {U}}\Vert ^{\varepsilon }_{\infty }$ be the unique $q\in \mathbb {C}$ such that for all $\delta>0$

$$ \begin{align*}\{ N<{\omega}\vert\ \vert\Vert v_{N}\Vert^{X_{\varepsilon}}_{\infty}-q\vert <\delta\}\in {\mathcal{U}}\end{align*} $$

if there is such a q and otherwise the value is $\infty $ (i.e., we do as before).

Now let $v=(\sum _{k=0}^{D_{N}-1}a^{N}_{k}u_{N}(k))_{N<{\omega }}/{\mathcal {U}}\in H^{u}$ . Then we let $\Vert v\Vert _{\infty }=\lim _{\varepsilon \rightarrow 0}\Vert v\Vert ^{\varepsilon }_{\infty }$ if there are $p<{\omega }$ and $W\in {\mathcal {U}}$ for which $\vert a^{N}_{k}(\xi _{N}(k))^{-1}\vert <p$ for all $N\in W$ and $k<D_{N}$ and otherwise we let $\Vert v\Vert _{\infty }=\infty $ . Notice that thus having bounded $\Vert \cdot \Vert _\infty $ -norm in $H^u$ requires the $\Vert \cdot \Vert ^S_\infty $ -norm to be bounded in a ${\mathcal {U}}$ -large set of $H_N$ s although the value is determined by what happens ‘close to $\sigma (A)$ ’. We then let $H^{m\infty }$ be the set of all $v\in H^{u}$ for which $\Vert v\Vert _{\infty }<\infty $ and $H^{m}_{\infty }=H^{m\infty }/\sim _{\infty }$ , where $\sim _{\infty }$ is the relation $\Vert v-u\Vert _{\infty }=0$ . We write $[f]_{\infty }$ for $f/{\mathcal {U}}/\sim _{\infty }$ .

The definition above may seem cumbersome, as we cannot restrict attention to the spectrum directly. This is because, although our measure will find the right spectrum eventually (cf. Lemma 3.12), our construction does not give any direct control of this convergence. Each $H_N$ has a discrete spectrum, but it is not even guaranteed that the eigenvalues in $H_N$ are in $\sigma (A)$ .

Lemma 5.6.

1. (i) For all $f\in C(S)$ , $F^u(f)\in H^{m\infty }$ and $\Vert f\Vert ^\sigma _{\infty }=\Vert F^u(f)\Vert _{\infty }$ .

2. (ii) Every element of $H^{m\infty }$ has finite $\lVert {\cdot }\rVert _2$ -norm, and for all $v\in H^u$ , $\lVert {v}\rVert ^u_0\leq \lVert {v}\rVert _2$ . For $f\in C(S)$ , $\lVert {F^u(f)}\rVert _0\leq \lVert {F^u(f)}\rVert _2\leq \lVert {F^u(f)}\rVert _\infty $ .

Proof. (i) The first claim is clear since f is bounded. For the second, we notice that f is uniformly continuous and thus the direction $\Vert f\Vert ^\sigma _{\infty }\ge \Vert F^u(f)\Vert _{\infty }$ follows easily. The direction $\Vert f\Vert ^\sigma _{\infty }\le \Vert F^u(f)\Vert _{\infty }$ follows from the equality of $\sigma (A)$ and $\tilde {\sigma }(A)$ (recall Definition 3.11) and the continuity of f.

(ii) The first claim is a straightforward calculation, the second follows from Hölder’s inequality, as $\mu (S)=1$ . The chain of inequalities follows from the classical result.

Let $H^{m}_{*}=\bigcup _{k\in \{ 0,2,\infty \}}H^{m}_{k}$ . We define a pairing $\langle \cdot |\cdot \rangle $ on $H^{m}_{*}$ the same way as before: For $[f]_{k},[g]_{r}\in H^{m}_{*}$ , $\langle [f]_{k}|[g]_{r}\rangle =q$ if $q\in \mathbb {C}$ is such that for all $f'\in [f]_{k}$ and $g'\in [g]_{r}$ , $\langle f'|g'\rangle ^{u}$ is infinitely close to q. If no such q exists we let $\langle [f]_{k}|[g]_{r}\rangle =\infty $ (meaning that $\langle [f]_{k}|[g]_{r}\rangle $ is not well-defined).

Lemma 5.7. If $x\in H^{m}_{\infty }$ and $y\in H^{m}_{0}$ , then $\langle x|y\rangle \ne \infty $ .

Proof. Let $x=[(x_{N})_{N<{\omega }}]_{\infty }$ , where

$$ \begin{align*}x_{N}=\sum_{n=0}^{D_{N}-1}a^{N}_{n}u_{N}(n)\end{align*} $$

and $y=[(y_{N})_{N<{\omega }}]_{0}$ , where

$$ \begin{align*}y_{N}=\sum_{n=0}^{D_{N}-1}b^{N}_{n}u_{N}(n)\end{align*} $$

and let $q>\Vert x\Vert _{\infty }$ and $r>\Vert y\Vert _{0}$ . Let $p<{\omega }$ , be such that for all $N<{\omega }$ and $n<D_{N}$ , $\vert a^{N}_{n}(\xi _{N}(n))^{-1}\vert <p$ . It is enough to show that

$$ \begin{align*}\vert \langle (x_{N})_{N<{\omega}}|(y_{N})_{N<{\omega}}\rangle\vert <qr.\end{align*} $$

Let $\varepsilon>0$ be such that $\Vert x\Vert ^{\varepsilon }_{\infty }<q$ . Then we choose $k<{\omega }$ so that there is a good $Y\subseteq Sq_{k}$ such that if as before we denote $S^{Y}_{0}=\cup _{R\in Y}\overline R$ and $S^{Y}_{1}=\cup _{R\in Sq_{k}-Y}\overline R$ , then $S-X_{\varepsilon }\subseteq S^{Y}_{1}$ . Then

$$ \begin{align*}\vert \langle x_{N}|y_{N}\rangle\vert\le\sum_{n=0}^{D_{N-1}}\vert a_{n}^{N}\vert\ \vert b^{N}_{n}\vert <\end{align*} $$

$$ \begin{align*}< \sum_{\lambda_{N}(n)\in S^{Y}_{0}}\xi_{N}(n)q\vert b^{N}_{n}\vert +\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)p\vert b^{N}_{n}\vert\le\end{align*} $$

$$ \begin{align*}\le q\sum_{\lambda_{N}(n)\in S^{Y}_{0}}\xi_{N}(n)\vert b^{N}_{n}\vert +p\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)\vert b^{N}_{n}\vert <qr +p\sum_{\lambda_{N}(n)\in S^{Y}_{1}}\xi_{N}(n)\vert b^{N}_{n}\vert\end{align*} $$

in a set of $N<{\omega }$ that belongs to ${\mathcal {U}}$ . Now the claim follows from the assumption that $(y_{N})_{N<{\omega }}/{\mathcal {U}}$ is $0$ -good.

Next we set out to find distributions as vectors in our space $H^u$ .

Definition 5.8. We say that an antilinear map $\theta :D(S)\rightarrow \mathbb {C}$ is a generalized distribution if it is bounded in the sense of $\Vert \cdot \Vert ^\sigma _{\infty }$ , i.e., there is $K<{\omega }$ such that $\vert \theta (f)\vert \le K\Vert f\Vert ^\sigma _{\infty }$ . Then $\theta $ extends to $C(S)$ by continuity and thus by generalized distributions we actually mean bounded antilinear maps $\theta :C(S)\rightarrow \mathbb {C}$ .

We now fix a generalized distribution $\theta $ for the remainder of this section.

In general a distribution emerges through its test functions, and we will construct test functions picking out rectangles in the spectrum, similarly to how the measure was built. This will let us ‘copy over’ the values of $\theta $ to our vector. However, we need to be careful to make sure our rectangles are well behaved.

Definition 5.9. We return to the lines $I_{r}$ and $J_{r}$ and to the sets $I_{r}^{\varepsilon }$ and $J_{r}^{\varepsilon }$ from Section 3. For $X\subseteq \mathbb {C}$ , we say that $f\in C(S)$ is an X-function if for all $x\in S$ , $\vert f(x)\vert \le 1$ and for all $x\in S-X$ , $f(x)=0$ . Notice that we do not require that $X\subseteq S$ but still $dom(f)=S$ .

We say that a line $I_{r}$ is good (for $\theta )$ if for all $\delta>0$ there is $\varepsilon>0$ such that for all $I^{\varepsilon }_{r}$ -functions f, $\vert \theta (f)\vert <\delta $ . $J_{r}$ being good is defined similarly.

Lemma 5.10. There are at most countably many $r\in [{-}M,M]$ such that $I_{r}$ is not good, and the same is true for the lines $J_{r}$ .

Proof. Suppose not. Then there are $\delta>0$ and $r_{i}$ , $i<{\omega }_{1}$ , such that for all $\varepsilon>0$ and $i<{\omega }_{1}$ , there is an $I^{\varepsilon }_{r_{i}}$ -function $f^{\varepsilon }_{i}$ such that $\vert \theta (f^{\varepsilon }_{i})\vert>\delta $ . W.l.o.g. we may assume that for all $i<{\omega }$ , $r_{i}<r_{i+1}$ . Then for all $i<{\omega }$ , we choose $\varepsilon _{i}>0$ so that for all $i<{\omega }$ , $r_{i}+\varepsilon _{i}<r_{i+1}-\varepsilon _{i+1}$ . Also w.l.o.g. we may assume that for all $i<{\omega }$ , the direction of $\lambda _{i}=\theta (f^{\varepsilon _{i}}_{i})$ is roughly the same, e.g., $Re(\lambda _{i})\ge Im(\lambda _{i})\ge 0$ . Let $f=\sum _{i<{\omega }}(1/(i+1))f^{\varepsilon _{i}}_{i}$ . Clearly $f\in C(S)$ and $\Vert f\Vert _{\infty }\le 1$ but $\theta (f)=\infty $ , a contradiction.

Definition 5.11. We say that $I_{r}$ is very good (for $\theta )$ if it is good and for all $\delta>0$ , there is $\varepsilon>0$ such that $\mu ^{n}(I^{\varepsilon }_{r})<\delta $ . $J_{r}$ being very good is defined similarly. We say that $\varepsilon>0$ is nice for r if both $r-\varepsilon $ and $r+\varepsilon $ are nice or ${<}{-}\,M$ or $>M$ .

Lemma 5.12.

1. (i) There are at most countably many $r\in [{-}M,M]$ such that $I_{r}$ is not very good and the same is true for lines $J_{r}$ .

2. (ii) For all r there are at most countably many $\varepsilon>0$ that are not nice for r.

3. (iii) If $\varepsilon>0$ is nice for r, then $\mu (I_{r}^{\varepsilon })=\mu ^{n}(I_{r}^{\varepsilon })$ and $\mu (J_{r}^{\varepsilon })=\mu ^{n}(J_{r}^{\varepsilon })$ .

Proof. (ii): This is immediate by Lemma 3.2.

(i): This is immediate by Lemmas 3.2 and 5.10.

(iii): This can be proved as Lemma 3.4(i) was proved.

Definition 5.13. For all $k<{\omega }$ , we choose $r^{k}_{i}\in [{-}M,M]$ , $i<2^{k+2}+1$ , so that:

1. (i) $r^{k}_{i}<r^{k}_{i+1}$ and $r_{i+1}^{k}-r^{k}_{i}<2M/(k+1)$ ,

2. (ii) $I_{r^{k}_{i}}$ and $J_{r^{k}_{i}}$ are very good for $\theta $ ,

3. (iii) $r^{0}_{0}\,{=}\,{-}M$ and $r^{0}_{4}=M$ ,

4. (iv) for all $i<2^{k+2}+1$ there is $j<2^{k+3}+1$ such that $r^{k}_{i}=r^{k+1}_{j}$ .

When we talk about $I^{\varepsilon }_{r^{k}_{i}}$ or $J^{\varepsilon }_{r^{k}_{i}}$ we assume that $\varepsilon $ is small enough so that for all $j<2^{k+2}$ , $r^{k}_{j}+\varepsilon <r^{k}_{j+1}-\varepsilon $ .

For all $k<{\omega }$ , $i,j<2^{k+2}$ and $\varepsilon>0$ , we let $B^{k}_{ij}=\{ \lambda \in S\vert \ r^{k}_{i}<Re(\lambda )<r^{k}_{i+1},\ r^{k}_{j}<Im(\lambda )<r^{k}_{j+1}\}$ and $R^{k}_{\varepsilon }=\cup _{i<2^{k+2}+1}(I^{\varepsilon }_{r^k_{i}}\cup J^{\varepsilon }_{r^k_{i}})$ . We say that $\varepsilon>0$ is very nice for $k<{\omega }$ , if it is nice for every $r^k_{i}$ , $i<2^{k+2}$ . As in Lemma 5.12, we can see that $\mu (B^{k}_{ij})=\mu ^{n}(B^{k}_{ij})$ , that if $\varepsilon $ is very nice for k, then $\mu (R^{k}_{\varepsilon })=\mu ^{n}(R^{k}_{\varepsilon })$ , and that excluding countably many $\varepsilon $ , every $\varepsilon $ is very nice for k.

Lemma 5.14. For all $k<{\omega }$ and $\delta>0$ , there is $\varepsilon>0$ such that $\mu (R^{k}_{\varepsilon })<\delta $ and for all $R^{k}_{\varepsilon }$ -functions f, $\vert \theta (f)\vert <\delta $ .

Proof. For all $R^{k}_{\varepsilon }$ -functions f there are $I^{\varepsilon }_{r^{k}_{i}}$ - and $J^{\varepsilon }_{r^{k}_{i}}$ -functions $f_{i}$ and $g_{i}$ , $i<2^{k+2}$ , such that $f=\sum _{i<2^{k+2}}(f_{i}+g_{i})$ . The only nontrivial part here are the ‘crossings’ between I and J lines, and there one can define $f_i$ to be any continuous continuation from the values it has on the upper and lower edge of the crossing and 0 on the left and right edge, and define g from the differences $f-f_i$ . Then the claim follows easily.

Definition 5.15. For all $\lambda \in \mathbb {C}$ , $k<{\omega }$ , $i,j<2^{k+2}$ and $\varepsilon>0$ , we choose a $B^{k}_{i,j}$ -function $f^{k\varepsilon \lambda }_{ij}$ so that for all $x\in \mathbb {C}$ , if $r^{k}_{i}+\varepsilon <Re(x)<r^{k}_{i+1}-\varepsilon $ and $r^{k}_{j}+\varepsilon <Im(x)<r^{k}_{j+1}-\varepsilon $ , then $f^{k\varepsilon \lambda }_{ij}(x)=\lambda $ . We then define $\theta (B^{k}_{ij},\lambda )$ to be $\lim _{\varepsilon \rightarrow 0}\theta (f^{k\varepsilon \lambda }_{ij})$ . Notice that this does not depend on the choice of functions $f^{k\varepsilon \lambda }_{ij}$ . Notice also that $\theta (B^{k}_{ij},\lambda )=\overline \lambda \theta (B^{k}_{i,j},1)$ .

Definition 5.16. Suppose $n:{\omega }\rightarrow {\omega }$ and $\varepsilon :{\omega }\rightarrow \mathbb {R}_{+}$ . We say that the pair $(n,\varepsilon )$ is $\theta $ -good if the following holds:

1. (i) For all $0<m<{\omega }$ , $\{ N<{\omega }\vert \ n(N)>m,\ \varepsilon (N)<1/m\}\in {\mathcal {U}}$ .

2. (ii) There is a $W=W(\theta ,n,\varepsilon )\in {\mathcal {U}}$ such that for all $N\in W$ if $n=n(N)>0$ , then the following holds: Let $\varepsilon =\varepsilon (N)>0$ , $\delta '=\delta '(N)=\min \{ \mu _{N}(B^{n}_{ij})\vert \ i,j<2^{n+2},\ \mu (B^{n}_{ij})>0\}$ where $\mu _{N}(B^{n}_{ij})=\sum _{\lambda _{N}(k)\in B^{n}_{ij}}\xi _{N}(k)^{2}$ , and let $\delta =\delta (N)=\delta '/(2^{3(n+2)})$ . Then:

   1. (a) for all $R^{n}_{\varepsilon }$ -functions f, $\vert \theta (f)\vert <\delta $ ,

   2. (b) $\sum _{\lambda _{N}(i)\in R^{n}_{\varepsilon }}\xi _{N}(i)^{2}<\delta $ ,

   3. (c) for all $i,j <2^{n+2}$ , $\vert \mu _{N}(B^{n}_{ij})-\mu (B^{n}_{ij})\vert <\delta $ .

3. (iii) $\varepsilon (N)$ is very nice for $n(N)$ .

Notice that if $(n,\varepsilon )$ is $\theta $ -good and for all $N<{\omega }$ , $0<\varepsilon ' (N)<\varepsilon (N)$ , and $\varepsilon '$ is very nice for $n(N)$ , then $(n,\varepsilon ')$ is $\theta $ -good. So keeping in mind that the set of $\varepsilon $ very nice for n is dense, we can always assume, e.g., that $\varepsilon (N)$ is such that for all $i<2^{n(N)+2}$ , $\varepsilon (N)<(r^{n(N)}_{i+1}-r^{n(N)}_{i})/3$ .

Lemma 5.17. There is a $\theta $ -good pair $(n,\varepsilon )$ for which we can choose $W(\theta ,n,\varepsilon )={\omega }$ .

Proof. Simply let $n(N)$ be the largest natural number $0<n\le N$ for which there is $\varepsilon =\varepsilon (N)$ for which Definition 5.16(ii) and (iii) hold, if such n and $\varepsilon $ exist and otherwise we let $n(N)=0$ and $\varepsilon =1$ . Since for all $\delta>0$ , $n<{\omega }$ and $i,j<2^{n+2}$ , the set

$$ \begin{align*}\{ N<{\omega}\vert\ \vert\mu_{N}(B^{n}_{ij})-\mu (B^{n}_{ij}\vert <\delta\}\end{align*} $$

belongs to ${\mathcal {U}}$ , it is easy to see that now also (i) holds.

Remark 5.18. The reader may wonder what the purpose of the sets $W(\theta ,n,\varepsilon )$ is. In the context when we have infinitely many generalized distributions $\theta $ to handle, we need to diagonalize and then these sets become handy, see Remarks 5.22 and 6.5.

Now we fix a $\theta $ -good pair $(n,\varepsilon )$ and in order to simplify the notations, we assume that $W(\theta ,n,\varepsilon )={\omega }$ .

We are finally ready to define the vector in $H^u$ that will correspond to the distribution $\theta $ :

Definition 5.19. We define $u(\theta )=(u_{N}(\theta ))_{N<{\omega }}/{\mathcal {U}}\in H^{u}$ by letting $n=n(N)$ and defining

$$ \begin{align*}u_{N}(\theta )=\sum_{\mu (B^{n}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n}_{ij}}(\xi_{N}(k)\theta (B^{n}_{ij},1)/\mu_{N}(B^{n}_{ij}))u_{N}(k).\end{align*} $$

Recall that we may assume the relevant $\mu _N(B^n_{ij})\neq 0$ , as this will happen for all N in some $W\in {\mathcal {U}}$ . Also notice that $u(\theta )$ is $0$ -good (immediate by the definition) and that for all $f\in C(S)$ , one can define a generalized distribution $\theta _{f}$ by $\theta _{f}(g)=\langle g|f\rangle $ and then (if $\theta =\theta _{f}$ ) $[F^u(f)]_{0}=[u(\theta _{f})]_{0}$ (easy calculation).

Lemma 5.20. $\Vert u(\theta )\Vert _{0}<\infty $ .

Proof. Let K be such that for all $f\in C(S)$ , $\vert \theta (f)\vert <K\Vert f\Vert ^\sigma _{\infty }$ . It is enough to show that for all $N<{\omega }$ ,

$$ \begin{align*}\sum_{\mu (B^{n}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n}_{ij}}\vert\xi_{N}(k)^{2}\theta (B^{n}_{ij},1)/\mu_{N}(B^{n}_{ij})\vert =\end{align*} $$

$$ \begin{align*}\sum_{\mu (B^{n}_{ij})\ne 0}\vert\theta (B^{n}_{ij},1)\vert\le 16K,\end{align*} $$

where $n=n(N)$ . Suppose not. Then one can find $X\subseteq \{ B^{n}_{ij}\vert \ i,j<2^{n+2},\ \mu (B^{n}_{ij})>0\}$ such that

$$ \begin{align*}\sum_{B\in X}\vert\theta (B,1)\vert>2K\end{align*} $$

and for all $B\in X$ , $\theta (B,1)$ point roughly to the same direction, e.g., $Re(\theta (B,1))\ge Im(\theta (B,1))\ge 0$ , see the proof of Lemma 5.10. But now for all $B\in X$ , choose a B-function $f_{B}$ so that $\theta (B,1)$ is very close to $\theta (f_{B})$ . Let $f=\sum _{B\in X}f_{B}\in C(S)$ . Then $\Vert f\Vert _{\infty }=1$ but $\vert \theta (f)\vert>K$ , a contradiction.

Theorem 5.21. For all $f\in C(S)$ , $\theta (f)=\langle [F^u(f)]_{\infty }|[u(\theta )]_{0}\rangle $ .

Proof. Let $f\in C(S)$ . W.l.o.g. we may assume that $\vert f(x)\vert \le 1$ for all $x\in S$ , in particular, $\Vert f\Vert ^\sigma _{\infty }\le 1$ . For all $0<n<{\omega }$ , there is $\varepsilon _{1}(n)$ such that if $x,y\in S$ are such that $\vert x-y\vert <4M/(n(N)+1)$ , then $\vert f(x)-f(y)\vert <\varepsilon _{1}(n(N))$ and $\varepsilon _{1}(n)$ goes to $0$ when n goes to infinity. Then for all $N<{\omega }$ such that $n(N)>0$ , we can find $f_{N}\in C(S)$ such that $\Vert f-f_{N}\Vert _{\infty }<\varepsilon _{1}(n(N))$ , $\vert f_{N}(x)\vert \le 1$ for all $x\in S$ and $f_{N}\restriction (B^{n(N)}_{ij}-R^{n(N)}_{\varepsilon (N)})$ is constant for all $i,j<2^{n+2}$ (here $\varepsilon (N)$ is the one from Definition 5.16, not $\varepsilon _{1}(n(N))$ ). Let $c^{N}_{ij}$ be the constant value. Now we notice that $\theta (f_{N})$ goes to $\theta (f)$ when $n(N)$ goes to infinity and also $\langle [F^u(f_{N})]_{\infty }|[u(\theta )]_{0}\rangle $ goes to $\langle [F^u(f)]_{\infty }|[u(\theta )]_{0}\rangle $ when $n(N)$ goes to infinity by the proof of Lemma 5.7 (and Lemma 5.20). Thus it is enough to show the following: Let $\varepsilon ^{*}>0$ and $N<{\omega }$ be such that $n(N)>0$ , and $K/n(N)<\varepsilon ^{*}$ where $K>0$ is a natural number such that $\vert \theta (f)\vert \le K\Vert f\Vert ^\sigma _{\infty }$ . Then

$$ \begin{align*}\vert \theta (f_{N})-\langle F_{N}(f_{N})|u_{N}(\theta)\rangle\vert \le 5\varepsilon^{*}.\end{align*} $$

We write $n=n(N)$ , $\varepsilon =\varepsilon (N)$ , $\delta =\delta (N)$ etc.

Now for all $i,j<2^{n+2}$ , there is a $B^{n}_{ij}$ -function $f_{ij}$ such that for all $x\in B^{n}_{i,j}-R^{n}_{\varepsilon }$ , $f_{ij}(x)=f_{N}(x)=c^{N}_{ij}$ . Let $f_{2}=\sum _{i,j<2^{n+2}}f_{ij}$ . Then (as $\delta <\varepsilon ^*$ ) it is enough to show that

$$ \begin{align*}\vert \theta (f_{2})-\langle F_{N}(f_{N})|u_{N}(\theta)\rangle\vert \le 4\varepsilon^{*} .\end{align*} $$

For this it is enough to show that for all $i,j <2^{n+2}$ ,

$$ \begin{align*}\vert \theta (f_{ij})-\langle F_{N}(f_{N}\restriction B^{n}_{i,j})|u_{N}(\theta)\rangle\vert \le 3K/(2^{3(n+2)}) ,\end{align*} $$

where by $F_{N}(f_{N}\restriction B^{n}_{i,j})$ we mean $\sum _{\lambda _{N}(k)\in B^{n}_{ij}}\xi _{N}(k)f_{N}(\lambda _{N}(k))u_{N}(k)$ .

Now if $\mu (B^{n}_{ij})=0$ , then $B^{n}_{ij}\cap \sigma (A)=\emptyset $ by the definition of $\tilde {\sigma }(A)$ and Lemma 3.12 and thus $\theta (f_{ij})=0$ since $f_{ij}$ is $\sim _{\infty }$ -equivalent with the constant zero function. Clearly then also $\langle F_{N}(f_{N}\restriction B^{n}_{i,j})|u_{N}(\theta )\rangle =0$ . Thus from now on we may assume that $\mu (B^{n}_{ij})>0$ .

But then it is enough to show that

$$ \begin{align*}\vert \theta (f_{ij})-\langle F_{N}(f_{ij})|u_{N}(\theta)\rangle\vert \le 2K/(2^{3(n+2)}),\end{align*} $$

since

1. (*) if $\mu (B^{n}_{ij})>0$ , then

   $$ \begin{align*}(\sum_{\lambda_{N}(k)\in B^{n}_{ij}\cap R^{n}_{\varepsilon}}\vert\xi_{N}(k)\vert^{2})/\mu_{N}(B^{n}_{ij})\le\delta/\delta'\le 1/(2^{3(n+2)}).\end{align*} $$

But then it is enough to show that

$$ \begin{align*}\vert \theta (B^{n}_{ij},c^{N}_{ij})-\langle F_{N}(f_{ij})|u_{N}(\theta)\rangle\vert \le K/(2^{3(n+2)}) .\end{align*} $$

Since $\theta (B^{n}_{ij}, c^{N}_{ij})=\overline {c^{N}_{ij}}\theta (B^{n}_{ij},1)=\overline {f_{ij}(x)}\theta (B^{n}_{ij},1)$ for any $x\in B^{n}_{ij}-R^{n}_{\varepsilon }$ , using $(*)$ above, this is easy.

Remark 5.22. The set of all generalized distributions form a vector space, we call it GDIS, under $(\theta +\theta ')(x)=\theta (x)+\theta '(x)$ and $q\theta (x)=\theta (\overline q x)$ . Let V be a subspace of this vector space of countable dimension and let $\theta _{i}$ , $i<{\omega }$ , be a basis of this subspace. Then one can do the construction for all these generalized distributions simultaneously: One can choose the reals $r^{n}_{j}$ so that the lines $I_{r^{n}_{j}}$ and $J_{r^{n}_{j}}$ are very good for every $\theta _{i}$ and then one can find a pair $(n,\varepsilon )$ so that it is $\theta _{i}$ -good for every $\theta _{i}$ and in fact a bit more: Although we don’t get one W set for all the $\theta _i$ , we can handle finitely many at a time. In Definition 5.16(ii)(a), one can require that for all $R^{n}_{\varepsilon }$ -functions f and $i<n$ , $\vert \theta _{i}(f)\vert <\delta /n^{2}$ (see the remark immediately after the definition). Then for all $\theta \in V$ , one defines $W(\theta ,n,\varepsilon )$ to be the set of all $N<{\omega }$ such that $n(N)>0$ and there are $a_{i}\in \mathbb {C}$ , $i<n(N)$ , such that $\vert a_{i}\vert \le n(N)$ and $\theta =\sum _{i<n(N)}a_{i}\theta _{i}$ . It is easy to see that by using these n and $\varepsilon $ , $\theta \mapsto u(\theta )$ is an embedding of V to $H^{m}_{0}$ so that Theorem 5.21 holds.

We can now compare our construction to a rigged Hilbert space. We have defined our distributions using $C(S)$ as test functions. However, our construction disregards what happens outside $\sigma (A)$ , and in practice we are looking at $C(\sigma (A))$ , which embeds into $H^m_\infty $ . The distributions then embed into $H^m_0$ , so we can dig out the rigged Hilbert space in our ultraproduct. However, the construction embedding distributions into $H^m_0$ can only handle countably many distributions at a time (the way we approximate the test functions over rectangles varies with the distributions), asking for a question to be posed:

Open question 4. Can one find an embedding of all of GDIS into $H^{m}_{0}$ so that Theorem 5.21 and everything in Section 5 hold for it?

Another natural question that arises is how canonical the norms $\lVert {\cdot }\rVert _\infty $ and $\lVert {\cdot }\rVert _0$ are, as they were constructed from the chosen cyclic vector $\phi $ . However, there is no reason to believe that different cyclic vectors would generate the same ultraproduct $H^u$ , so different norms act on different spaces. The crucial thing is that we have shown that the vectors corresponding to distributions behave in the desired way (as distributions). Thus, e.g., computing kernels (the way we consider in the next section) in spaces arising from different cyclic vectors will give the same result.

6 Dirac delta functions and the Feynman propagator

We now turn to the study of the Feynman propagator. In [6] we studied the kernel vs. Feynman propagator for two simple quantum mechanical systems. To explain the terminology, let us consider a particle in (one-dimensional) space. Its state can be described by a wave function $\varphi $ in position space, where the amplitude $\varphi (x)$ determines the particle’s probability of being in position x. The evolution over a given time interval is described by the propagator $K(x,y)$ which expresses the probability amplitude of the particle traveling form point x to point y in the given time. (Usually the time is given as a third parameter, but with a time independent evolution operator, the question of calculating the kernel can be studied over a fixed time interval.) If the system has eigenvectors $\lvert {x}\rangle $ , $\lvert {y}\rangle $ , corresponding to the positions, one can calculate the propagator as an inner product

$$ \begin{align*}K(x,y)=\langle{y}\rvert K^{\Delta t}\lvert{x}\rangle, \end{align*} $$

where $K^{\Delta t}$ is the time evolution operator for the given time interval. In a system without eigenvectors, the propagator is defined as the kernel of the integral representation of the time evolution operator

$$ \begin{align*}K^{\Delta t}(\varphi)(y)=\int_{\mathbb{R}} K(x,y)\varphi(x)dx. \end{align*} $$

In [6] we built eigenvectors for the position and momentum operator in an ultraproduct model, by taking ultraproducts of eigenvectors in finite dimensional models. We tried to use them to calculate the propagator $\langle {y}\rvert K\lvert {x}\rangle $ in two cases, that of the free particle and that of the harmonic oscillator. However, it turned out that if one calculates the propagators in the finite dimensional models, one encounters divisibility issues, and the answer one gets is either 0 or the correct value scaled by a constant, where the constant depends on the physical system being modeled, and the answer on whether the constant divides the scaled distance of x and y, $\sqrt {N}(x-y)$ , where N is the dimension of the space. One might at first argue that this divisibility problem should disappear with large enough N (the method is only used for rational x and y, and our filter picks out highly divisible Ns), but the situation is not that straightforward. The way the eigenvectors are built in the ultraproduct, we get for each position x continuum many eigenvectors orthogonal to each other, as one can choose different sequences of eigenvectors, whose eigenvalues converge to x. And in such a sequence one cannot guarantee divisibility along the way. Thus, instead of using the propagators in the finite dimensional structures directly, we ended up using them to calculate the kernel instead: we computed averages of propagator values over small areas, and only in the ultraproduct looked at the limit as these areas approached zero.

In this section we present a way of defining Dirac deltas so that one can calculate the kernel as a propagator. Being able to find Dirac deltas is one of the main motivations for working in our general ultraproduct and looking at different norms instead of just working with $H^m_2$ . However, the way we define the Dirac deltas from distributions, has built into it the same averaging idea from [6] (Sections 3.2 and 3.3) that we described above. An easier way of calculating the kernel is a kind of midway between the approaches: We can find approximations of the Dirac deltas already in $H^m_2$ , and if the kernel exists and is continuous, it can be calculated as a limit of inner products taken in the finite dimensional models. We start by presenting this method.

So suppose B is an operator in H. Let $G^{-r}:H\rightarrow L_{2}(\sigma (A),\mu \restriction \sigma (A))$ be the isometric isomorphism determined by the following: for all $f\in C(S)$ , $G^{-r}(G(f))=f\restriction \sigma (A)$ . Let $G^{r}$ be the inverse of $G^{-r}$ and $B_{D}=G^{-r}BG^{r}$ . We suppose that B is such that there is a continuous function $K(x,y):\sigma (A)^{2}\rightarrow \mathbb {C}$ such that for all polynomials $P\in \mathbb {C} [X,Y]$ , there is a continuous $g\in B_{D}(f_{P})$ such that for all ${y\in \sigma (A)}$ , $g(y)=\int _{\sigma (A)}K(x,y)(f_{P}\restriction \sigma (A))(x))dx$ . We will write $B_{D}(f_{P})$ also for this continuous g. Notice that from these assumptions it follows, e.g., that B is bounded and that for all $f\in D(S)$ , $B_{D}(f)\in C(S)$ .

As justification for our assumptions, note that if we are going to calculate the kernel of B in the ‘spectral basis of A’, it makes sense to assume that B has one. As for continuity, the motivation of these questions comes from physics where most phenomena are modeled by continuous functions, especially when approximating methods are concerned. For example, the propagator of the free particle and the harmonic oscillator are continuous for nontrivial cases (meaning the time difference and angular frequency are nonzero). In the trivial case, the time evolution operator is just the identical operator, which does not have a continuous kernel. Here, if one would try to calculate with our Dirac deltas, one would get a function $K(x,y)$ that is 0 when $x\neq y$ and not defined (infinite) for $x=y$ . As our method only produces functions $\sigma (A)^2\to \mathbb {C}$ as kernels, this is the closest we can get to the solution one sees in physics text books, but it is not a proper kernel representation, and we have not pursued this direction. Thus we are assuming that K is not only measurable but even continuous.

However, we want to work in $L_{2}(S,\mu )$ in place of $L_{2}(\sigma (A),\mu \restriction \sigma (A))$ . For this we choose a continuation of K to $S^{2}$ and we call this continuation also K and we call $G^{-1}BG$ also $B_{D}$ and we notice that for all polynomials $P\in \mathbb {C} [X,Y]$ , $g(y)=\int _{S}K(x,y)f_{P}(x)dx$ belongs to $B_{D}(f_{P})$ , since

$$ \begin{align*}\int_{\sigma (A)}K(x,y)(f_{P}(x)\restriction\sigma (A))dx=(\int_{S}K(x,y)f_{P}(x)dx)\restriction\sigma (A)\end{align*} $$

as one can easily see and again call also this function $B_{D}(f_{P})$ . If we want to do the calculations in the finite dimensional spaces $H_{N}$ we need to find suitable operators $B_{N}$ on these spaces.

Although we later will end up working with generalized distributions $\theta $ (and then need to look in $H^u$ with various norms), the approximating kernel method we are adopting from [6, Section 3] works also inside $H^{m}$ (in fact in $H^{Im}$ as we will see) which appears a more natural place to work, and so we start by looking at the $L_{2}$ -norm. When we move to Dirac deltas we will need stronger assumptions. Our first assumption on the operators $B_{N}$ is the following:

1. (C1) There is a natural number $K_{D}$ such that for all $N<{\omega }$ and $v\in H_{N}$ ,

   $$ \begin{align*}\Vert B_{N}(v)\Vert <K_{D}\Vert v\Vert .\end{align*} $$

Notice that from this (C1) it follows that the ultraproduct $B^{u}$ of the operators $B_{N}$ gives a well-defined bounded operator on all of $H^{m}$ . We call this operator $B^{m}$ .

The second assumption is the obvious requirement that if we write $B^{Im}$ for the restriction of $B^{m}$ to $H^{Im}$ , then

1. (C2) $B^{Im}=G^{m}B(G^{m})^{-1}$ (= $F^mB_{D}(F^m)^{-1}$ ).

So how can one find the operators $B_{N}$ ? First of all, in fact, they need not be linear functions as long as the ultraproduct of them is nice enough. However in practice one probably wants them to be operators. Examples of finding these can be found in [6], although the situation there is not exactly the same as here. In the case of the free particle [6, Section 3.1], B had a definition in terms of an operator C for which we already had operators $C_{N}$ and we used this definition in the spaces $H_{N}$ to get operators $B_{N}$ . In the case of the harmonic oscillator we could have done essentially the same. However it turned out that with this definition $K(x,y)$ was very difficult to calculate. Thus we used another method that gave completely different operators $B_{N}$ but whose ultraproduct was the same (upto $\sim _{2}$ ) in the places that mattered (see [6, Section 3.3]).

In the next lemma we show that the operators $B_{N}$ always exist. The proof is existential, i.e., the method used there cannot be used to find the operators in practice, unless one already knows the value of the kernel. Also, as pointed out above, the best way of choosing the operators may be such that it gives operators that are very different from those chosen in the proof of the lemma. In [6, Section 3.3] there is an example of using operators, that are wrong in almost all the finite dimensional models, and whose ultraproduct thus is wrong also in the full metric ultraproduct, but for which the restriction to the image of the original model (corresponding to $H^{Im}$ here) is correct.

The operators defined in the proof will be useful later, as it will turn out they are even better behaved than required here.

Lemma 6.1. There are operators $B_{N}$ in the spaces $H_{N}$ such that they satisfy $($ C1 $)$ and $($ C2 $)$ above.

Proof. We define $B_{N}$ as follows. Let $v=\sum _{n=0}^{D_{N}-1}a_{n}u_{N}(n)\in H_{N}$ . Then we let

$$ \begin{align*}B_{N}(v)=\sum_{n=0}^{D_{N}-1}\sum_{k=0}^{D_{N}-1}\xi_{N}(k)\xi_{N}(n)a_{k}K(\lambda_{N}(k),\lambda_{N}(n))u_{N}(n).\end{align*} $$

Clearly $B_{N}$ is a linear function.

Let $K_{D}$ be a natural number greater than any of the absolute values of the values of the function K. Then

$$ \begin{align*}\Vert B_{N}(v)\Vert^2_{2}\le\sum_{n=0}^{D_{N}-1}\sum_{k=0}^{D_{N}-1}\xi_{N}(k)^{2}\xi_{N}(n)^{2}\vert a_{k}K(\lambda_{N}(k),\lambda_{N}(n))\vert^{2}\le\end{align*} $$

$$ \begin{align*}\le K_{D}^{2}\Vert v\Vert^2_{2}\sum_{n=0}^{D_{N}-1}\xi_{N}(n)^{2}=K_{D}^{2}\Vert v\Vert^2_{2}.\end{align*} $$

So (C1) holds.

From the definition of the functions $B_{N}$ and the uniform continuity of the functions K and $f_{P}$ , it is easy to see that for all $P\in \mathbb {C} [X,Y]$ , $[(B_{N}(F_{N}(f_{P})))_{N<{\omega }}]_{2}=[(F_{N}(B_{D}(f_{P})))_{N<{\omega }}]_{2}$ . But then (C2) follows (since the vectors $[(F_{N}(f_{P}))_{N<{\omega }}]_{2}$ , $P\in \mathbb {C} [X,Y]$ , are dense in $H^{Im}$ ).

From now on we will write $\tilde {B}_{N}$ for the operators $B_{N}$ from the proof of Lemma 6.1 $\tilde {B}^{u}$ for their ultraproduct and $\tilde {B}^{m}$ for their metric ultraproduct.

Now we want to calculate $K({\alpha } ,{\beta } )$ for ${\alpha } ,{\beta }\in \sigma (A)$ from operators $B_{N}$ , $N<{\omega }$ , that satisfy (C1) and (C2). We start by looking at the method used in [6], namely computing the kernel as a limit of approximate kernels (or propagators, as computed in the finite dimensional spaces). The Dirac delta method will be developed as a consequence. Now we choose numbers $r^{n}_{i}$ for $n<{\omega }$ and $i<2^{n+2}+1$ (and lines $I_{r^{n}_{i}}$ and $J_{r^{n}_{i}}$ ) as in Section 5 so that Definition 5.13 holds when (ii) is replaced by

(ii)’ for all $m<{\omega }$ , neither ${\alpha }$ nor ${\beta }$ is in any line $I_{r^{m}_{i}}$ or $J_{r^{m}_{i}}$ , $i<2^{m+2}+1$ , and for all $\delta>0$ there is $\varepsilon>0$ such that $\mu ^{n}(R^{m}_{\varepsilon })<\delta $ , where $R^{m}_{\varepsilon }$ is as in Section 5.

For all $p<{\omega }$ , we let $B^p_{\alpha }$ be the $B^p_{ij}$ containing ${\alpha }$ , and let $u^{p}_{{\alpha }}=(u^{p}_{{\alpha }}(N))_{N<{\omega }}/{\mathcal {U}}$ , where

$$ \begin{align*}u^{p}_{{\alpha}}(N)=\sum_{\lambda_{N}(k)\in B^{p}_{{\alpha}}}(\xi_{N}(k)/\mu_{N}(B^{p}_{{\alpha}}))u_{N}(k)\end{align*} $$

and similarly for ${\beta }$ in place of ${\alpha }$ . Notice that $\Vert u^{p}_{{\alpha }}\Vert ^2_{2}=1/\mu (B^{p}_{{\alpha }})$ and thus $[u^{p}_{{\alpha }}]_{2}\in H^{m}_{2}$ whenever ${\alpha }\in \sigma (A)$ .

Theorem 6.2. When ${\alpha },{\beta }\in \sigma (A)$ , $K({\alpha } ,{\beta } )=\lim _{p\rightarrow \infty }\langle [u^{p}_{{\beta }}]_{2}\vert B^{m}([u^{p}_{{\alpha }}]_{2})\rangle $ .

Proof. We write $\chi _{B^{n}_{ij}}$ for the characteristic function of $B^{n}_{ij}$ and $\chi ^{\prime }_{B^{n}_{ij}}$ for the function $\chi ^{\prime }_{B^{n}_{ij}}(x)=\chi _{B^{n}_{ij}}(x)/\mu (B^{n}_{ij})$ . Since we can approximate $\chi ^{\prime }_{B^{p}_{{\alpha }}}$ by polynomials in the $L_{2}$ -norm, it is easy to see that

$$ \begin{align*}[F^u(\chi^{\prime}_{B^{p}_{{\alpha}}})]_{2}=[u^{p}_{{\alpha}}]_{2}.\end{align*} $$

Notice that from this it follows that $[u^{p}_{{\alpha }}]_{2}\in H^{Im}$ . Now using this, the approximations again, (C1), (C2) and the proof of Lemma 6.1,

$$ \begin{align*}B^{m}([u^{p}_{{\alpha}}]_{2})=\tilde{B}^{m}([u^{p}_{{\alpha}}]_{2})=[\tilde{B}^{u}(u^{p}_{{\alpha}})]_{2}.\end{align*} $$

We are left with an easy calculation:

$$ \begin{align*} \langle u^{p}_{{\beta}}(N)\vert &\tilde{B}_{N}(u^{p}_{{\alpha}}(N))\rangle=\\ =\langle \sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}(\xi_{N}(k)/\mu_{N}(B^{p}_{{\beta}}))u_{N}(k)\vert& \\ \sum_{n=0}^{D_{N}-1}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}} K(\lambda_{N}(l),\lambda_{N}(n))& \xi_{N}(l)^{2}\xi_{N}(n)\mu_{N}(B^{p}_{{\alpha}})^{-1}u_{N}(n)\rangle =\\ =\sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}} K(\lambda_{N}(l),\lambda_{N}(k))&\xi_{N}(l)^{2}\xi_{N}(k)^{2}(\mu_{N}(B^{p}_{{\alpha}})\mu_{N}(B^{p}_{{\beta}}))^{-1}. \end{align*} $$

Now keeping in mind that K is a continuous function, when p is large enough, this is roughly

$$ \begin{align*}\sum_{\lambda_{N}(k)\in B^{p}_{{\beta}}}\sum_{\lambda_{N}(l)\in B^{p}_{{\alpha}}}K({\alpha},{\beta})\xi_{N}(l)^{2}\xi_{N}(k)^{2}(\mu_{N}(B^{p}_{{\alpha}})\mu_{N}(B^{p}_{{\beta}}))^{-1}=K({\alpha} ,{\beta}),\end{align*} $$

since the absolute value of the error is at most the maximum of

$$ \begin{align*}\vert K({\alpha} ,{\beta} )-K(\lambda_{N}(l),\lambda_{N}(k))\vert ,\end{align*} $$

for $\lambda _{N}(k)\in B^{p}_{{\beta }}$ and $\lambda _{N}(l)\in B^{p}_{{\alpha }}$ as a straightforward calculation shows.

Now we can turn to Dirac deltas. We let $\theta _{{\alpha }}$ be the generalized distribution such that $\theta _{{\alpha }}(f)=f({\alpha } )$ for all $f\in C(S)$ and $\theta _{{\beta }}$ is defined similarly. Now it is easy to see that for all $n<{\omega }$ and $i<2^{n+2}+1$ , the $I_{r^{n}_{i}}$ and $J_{r^{n}_{i}}$ chosen above for Theorem 6.2 are very good for both $\theta _{{\alpha }}$ and $\theta _{{\beta }}$ , i.e., all the requirements of Definition 5.13 are satisfied. It follows that we can find a pair $(n,\varepsilon )$ so that it is $\theta _{{\alpha }}$ -good and $\theta _{{\beta }}$ -good (see the end of Section 5). We will need one more requirement for the pair $(n,\varepsilon )$ . We will return to this once we have looked at the requirements for the operators $B_{N}$ , $N<{\omega }$ .

Again, recall that the pair $(n,\varepsilon )$ determines the function u (see Definition 5.19) and (independent of the last requirement) notice that $\Vert u(\theta _{{\alpha }})\Vert ^{u}_{0}=1$ and thus $[u(\theta _{{\alpha }})]_{0}\in H^{m}_{0}$ (and similarly for ${\beta }$ ). However $\Vert u(\theta _{{\alpha }})\Vert _{\infty }$ is infinite (unless $\alpha $ is an actual eigenvalue), as we can see below:

$$ \begin{align*} u_{N}(\theta_{\alpha} )&=\sum_{\mu (B^{n(N)}_{ij})\ne 0}\sum_{\lambda_{N}(k)\in B^{n(N)}_{ij}}(\xi_{N}(k)\theta_{\alpha} (B^{n(N)}_{ij},1)/\mu_{N}(B^{n(N)}_{ij}))u_{N}(k)\\ &=\left\{\begin{array}{ll} \sum_{\lambda_{N}(k)\in B^{n(N)}_{{\alpha}}}(\xi_{N}(k)/\mu_{N}(B^{n(N)}_{{\alpha}}))u_{N}(k), &\text{if }\mu(B^{n(N)}_{\alpha})\ne 0,\\ 0,&\text{otherwise.}\end{array}\right. \end{align*} $$

Now (assuming $\mu (B^{n(N)}_{\alpha })\ne 0$ , which by Lemma 3.12 happens in an ${\mathcal {U}}$ -large set as long as ${\alpha }\in \sigma (A)$ , which is the case relevant for Dirac deltas),

$$ \begin{align*}\Vert u_{N}(\theta_{\alpha} ) \Vert^{X_\varepsilon}_\infty=\sup\{1/\mu_{N}(B^{n(N)}_{{\alpha}}) \mid \lambda_{N}(k)\in B^{n(N)}_{{\alpha}}\cap X_\varepsilon\}. \end{align*} $$

But, unless ${\alpha }$ is an eigenvalue, $\mu _N(B^{n(N)}_{\alpha })$ will become arbitrary small, making $\Vert u(\theta _{{\alpha }})\Vert ^\varepsilon _{\infty }$ infinite (see Definition 5.5), and this causes problems, as the inner product in the Feynman propagator may not be well-defined. So we need to modify the assumptions (C1) and (C2).

We let $H^{\infty }_{\infty }$ be $H^{u}/\sim _{\infty }$ . This is a natural space to consider Dirac deltas, as it is large enough to allow for ‘infinite’ objects, and on the other hand has a very delicate equivalence class structure, avoiding the risk of putting into the same equivalence class objects that behave differently in our calculations. Now our first assumption requires that the ultraproduct of the operators $B_{N}$ gives a well-defined operator on $H^{\infty }_{\infty }$ . We will call the operator $B^{\infty }$ :

1. (C1)’ There is a natural number $K_{D}$ such that for all $N<{\omega }$ and $v\in H_{N}$ ,

   $$ \begin{align*}\Vert B_{N}(v)\Vert^{S}_{\infty} <K_{D}\Vert v\Vert^{S}_{\infty}.\end{align*} $$

Our second assumption ties the values of $B_{N}$ to values of $B_{D}$ in the sense of $\Vert \cdot \Vert _{\infty }$ . Here we use basically the simple functions since our definition of the function u is based on them. However, notice that instead of simple functions we could use polynomials here as well as in Section 5, but this would make the definition of u much more complicated.

We write $F^u(\chi ^{\prime }_{B^{n}_{ij}})$ for $(F_{N}(\chi ^{\prime }_{B^{n}_{ij}}))_{N<{\omega }}/{\mathcal {U}}$ where

$$ \begin{align*}F_{N}(\chi^{\prime}_{B^{n}_{ij}})=\sum_{n=0}^{D_{N}-1}\xi_{N}(n)\chi^{\prime}_{B^{n}_{ij}}(\lambda_{N}(n))u_N(n).\end{align*} $$

We also write $B_{D}(\chi ^{\prime }_{B^{n}_{ij}})$ for the function $g(y)=\int _{S}K(x,y)\chi ^{\prime }_{B^{n}_{ij}}(x)dx$ . Then (C2) implies

$$ \begin{align*}B^{m}([F^u(\chi_{B^{n}_{ij}})]_{2})=[F^u(B_{D}(\chi_{B^{n}_{ij}})]_{2}.\end{align*} $$

And now following this we assume:

1. (C2)’ For all $B^{n}_{ij}$ ,

   $$ \begin{align*}B^{\infty}([F^u(\chi^{\prime}_{B^{n}_{ij}})]_{\infty})=[F^u(B_{D}(\chi^{\prime}_{B^{n}_{ij}}))]_{\infty}.\end{align*} $$

We recall that if $\Vert (v_{N})_{N<{\omega }}/{\mathcal {U}}\Vert _{\infty }<\infty $ and for all $N<{\omega }$ , $v_{N}=\sum _{n=0}^{D_{N}-1}a^{N}_{n}u_{N}(n)$ , then there are $W\in {\mathcal {U}}$ and a natural number p such that for all $N\in W$ and $n<D_{N}$ , $\vert \xi _{N}(n)^{-1}a^{N}_{n}\vert <p$ . However, $B^{\infty }$ images of Dirac’s deltas don’t necessarily have this property. The values may not have a uniform bound for all N. For suitably chosen $H^m_0$ -vectors one could still get finite values from the pairing function, but this would be kind of accidental, like getting arbitrary values for a product like $0\cdot \infty $ . We suspect one could build a situation where (C1)’, (C2)’, and (*) below holds, and $u(\theta _{{\alpha }})$ and $u(\theta _{{\beta }})$ give Feynman’s propagator the value $K({\alpha } ,{\beta } )$ , but for this kind of wrong reason. So we introduce one more requirement for the operators $B_{N}$ (it is a bit unnecessarily strong, but we are just making a point).

1. (C3)’ There is a natural number p such that for all $n<{\omega }$ , $i,j<2^{n+2}+1$ and $N<{\omega }$ , $\Vert B_{N}(u^{n}_{ij}(N))\Vert ^{S}_{\infty }<p$ , where

   $$ \begin{align*}u^{n}_{ij}(N)=\sum_{\lambda_{N}(k)\in B^{n}_{ij}}(\xi_{N}(k)/\mu_{N}(B^{n}_{ij}))u_{N}(k),\end{align*} $$
   when $\mu _N(B^n_{ij})\neq 0$ , and 0 otherwise.

Lemma 6.3. The operators $\tilde {B}_{N}$ , $N<{\omega }$ , satisfy $($ C1 $)$ ’, $($ C2 $)$ ’, and $($ C3 $)$ ’.

Proof. (C1)’ and (C2)’ can be proved essentially as in the proof of Lemma 6.1 and (C3)’ is a straightforward calculation.

Let us return to the choice of the pair $(n,\varepsilon )$ and thus to the choice of u. We choose it so that in addition to what we have already said, the following holds: There are $W(\theta _{{\alpha }},n,\varepsilon )$ and $W(\theta _{{\beta }},n,\varepsilon )$ that witness that $(n,\varepsilon )$ is both $\theta _{{\alpha }}$ -good and $\theta _{{\beta }}$ -good and

1. (*) if $N\in W(\theta _{{\alpha }},n,\varepsilon )\cap W(\theta _{{\beta }},n,\varepsilon )$ and $p=n(N)>0$ , then

   $$ \begin{align*}\vert \langle u^{p}_{{\beta}}(N)\vert B_{N}(u^{p}_{{\alpha}}(N))\rangle-\langle u^{p}_{{\beta}}\vert B^{u}(u^{p}_{{\alpha}})\rangle\vert <p^{-1}.\end{align*} $$

It is easy to see that this is possible.

Proposition 6.4. Suppose $($ C1 $)$ ’, $($ C2 $)$ ’ and $($ C3 $)$ ’ hold, and ${\alpha },{\beta }\in \sigma (A)$ . Then

$$ \begin{align*}K({\alpha} ,{\beta} )=\langle [u(\theta_{{\beta}})]_{0}| B^{\infty}([u(\theta_{{\alpha}})]_{\infty})\rangle.\end{align*} $$

Proof. Notice that if $p=n(N)>0$ , then $F_N(\chi _{B^p_{\alpha }}\mu _N(B^p_{\alpha })^{-1})=u^{p}_{{\alpha }}(N)=u_{N}(\theta _{{\alpha }})$ and $(F_N(\chi _{B^p_{\alpha }}\mu _N(B^p_{\alpha })^{-1}))_{N<{\omega }}/{\mathcal {U}}\in [F^u(\chi ^{\prime }_{B^p_{\alpha }})]_\infty $ . and so from (C3)’ it follows that $B^{\infty }[u(\theta _{{\alpha }})]_{\infty }\in H^{m}_{\infty }$ and thus by Lemma 5.7,

$$ \begin{align*}\langle [u(\theta_{{\beta}})]_{0}| B^{\infty}([u(\theta_{{\alpha}})]_{\infty})\rangle=\overline{\langle B^{\infty}([u(\theta_{{\alpha}})]_{\infty})|[u(\theta_{{\beta}})]_{0}\rangle}<\infty ,\end{align*} $$

i.e., it is well-defined. By (C2)’ and Lemma 6.3, $B^{\infty }([u^{n}_{{\alpha }}]_{\infty })=[\tilde {B}^{u}(u^{n}_{{\alpha }})]_{\infty }$ , for all $n<{\omega }$ . But then the claim follows from (the proof of) Theorem 6.2 and (*) above.

Remark 6.5. Let Z be the set of all r for which there is $\delta>0$ such that either for all $\varepsilon>0$ $\mu ^{n}(I_{r}^{\varepsilon })\ge \delta $ or for all $\varepsilon>0$ , $\mu ^{n}(J^{\varepsilon }_{r})\ge \delta $ . In Section 3 we saw that Z is countable. Let $Y=\cup _{r\in Z}(I_{r}\cup J_{r})$ . Then as in the end of Section 5, we can see that for any countable $X\subseteq \sigma (A)-Y$ , we can choose a pair $(n,\varepsilon )$ so that it is $\theta _{{\alpha }}$ -good for all ${\alpha }\in X$ , i.e., Theorem 5.21 holds, (*) above holds for every pair $({\alpha },{\beta } )\in X^{2}$ and in addition u gives an embedding of the vector space generated by the Dirac deltas $\theta _{{\alpha }}$ , ${\alpha }\in X$ , into $H^{m}_{0}$ . So we can make everything in Sections 4 and 5 work for all $\theta _{{\alpha }}$ , ${\alpha }\in X$ , simultaneously. If X is dense in $\sigma (A)$ , one expects that this is enough for most arguments in the contexts where the essential phenomena are modeled by continuous functions.

7 The non-cyclic case

We finally look at the case where the operator doesn’t have a cyclic vector. Then H can be decomposed into a countable direct sum $\bigoplus _{i<\omega } H_i$ of subspaces $H_i$ , invariant under A and with a cyclic vector $v_i$ . By the construction for the cyclic case, each $H_i$ is isomorphic to a space $L_2(S,\mu _i)$ , where every $\mu _i$ is a Borel measure with $\mu _i(S)=1$ .

Now, to combine these, let

$$ \begin{align*}\mu=\sum_{i=0}^{\infty} 2^{-i-1}\mu_i. \end{align*} $$

Then $\mu $ is a finite Borel measure, and every $\mu _i$ is absolutely continuous with respect to $\mu $ . Thus by the Radon–Nikodym theorem there are Borel functions $f_i$ such that for all Borel sets $A\subseteq S$

$$ \begin{align*}\mu_i(A)=\int_Af_id\mu. \end{align*} $$

This means that each $L_2(S,\mu _i)$ can be isometrically embedded into $L_2(S,\mu )$ by the mapping generated by

$$ \begin{align*}g(x)\mapsto \sqrt{f_i(x)}g(x). \end{align*} $$

Now if we wish to combine the direct sum of these into an $L_2$ space over a finite measure space, we can turn to the Bochner spaces, which are function spaces of vector valued functions (see, e.g., [7]). We can recognize the space $\oplus _{i<\omega }L_2(S,\mu )$ as a Bochner- $\ell _2$ -space with values in the space $L_2(S,\mu ;\mathbb {C})$ , i.e., $\ell _2(L_2(S,\mu ;\mathbb {C}))$ . By [7, Corollary 1.2.23] $\ell _2(L_2(S,\mu ;\mathbb {C}))\cong L_2(S,\mu ;\ell _2(\mathbb {C}))$ , where the latter is the vector valued $L_2$ -space over S with values in $\ell _2(\mathbb {C})$ . Our sum space $\oplus _iH_i$ can now be isometrically embedded into this space by combining the isometric isomorphisms $H_i\cong L_2(S,\mu _i)$ obtained from our previous theory, the embeddings $L_2(S,\mu _i)\hookrightarrow L_2(S,\mu )$ , and finally the isomorphism $\ell _2(L_2(S,\mu ;\mathbb {C}))\cong L_2(S,\mu ;\ell _2(\mathbb {C}))$ .

If we denote the image under this embedding by $H'$ , we can as before find a copy of $H'$ within a suitable ultraproduct of finite-dimensional spaces: If we denote by $H^i_N$ the finite dimensional subspaces of $H_i$ constructed as before, we can construct spaces

$$ \begin{align*}H^N=\oplus_{i\leq N}H^i_N, \end{align*} $$

and build the ultraproduct model from these. A canonical modification of the embedding $G^m$ gives an embedding of $\oplus _{i<\omega }H_i$ (and thus of $H'$ ) into the metric ultraproduct and allows us to use finite dimensional approximations. It is worth noting that this does not give an embedding of all of $L_2(S,\mu ;\ell _2(\mathbb {C}))$ into the metric ultraproduct.

Now, although we can find a spectral decomposition of our space in an ultraproduct of finite-dimensional spaces, we don’t see that this would give a general approach to kernels. If the operator B behaves differently in the different spaces $H_i$ , one doesn’t get a common complex-valued kernel that could be used for the vectors of the Bochner space. And if the $H_i$ aren’t invariant under B, one cannot treat these spaces separately, either.