THE ONTO MAPPING OF SIERPINSKI AND NONMEAGER SETS

Abstract

The principle (*) of Sierpinski is the assertion that there is a family of functions 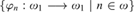$\left\{ {{\varphi _n}:{\omega _1} \to {\omega _1}|n \in \omega } \right\}$ such that for every 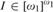$I \in {[{\omega _1}]^{{\omega _1}}}$ there is n ε ω such that 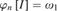${\varphi _n}[I] = {\omega _1}$. We prove that this principle holds if there is a nonmeager set of size ω₁ answering question of Arnold W. Miller. Combining our result with a theorem of Miller it then follows that (*) is equivalent to 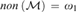$non\left( {\cal M} \right) = {\omega _1}$. Miller also proved that the principle of Sierpinki is equivalent to the existence of a weak version of a Luzin set, we will construct a model where all of these sets are meager yet 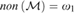$non\left( {\cal M} \right) = {\omega _1}$.