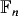Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ioana, Adrian
Peterson, Jesse
and
Popa, Sorin
2008.
Amalgamated free products of weakly rigid factors and calculation of their symmetry groups.
Acta Mathematica,
Vol. 200,
Issue. 1,
p.
85.
Sasyk, Roman
and
Törnquist, Asger
2009.
The classification problem for von Neumann factors.
Journal of Functional Analysis,
Vol. 256,
Issue. 8,
p.
2710.
Sasyk, Román
and
Törnquist, Asger
2009.
Borel Reductibility and Classification of von Neumann Algebras.
The Bulletin of Symbolic Logic,
Vol. 15,
Issue. 2,
p.
169.
KITTRELL, JOHN
and
TSANKOV, TODOR
2010.
Topological properties of full groups.
Ergodic Theory and Dynamical Systems,
Vol. 30,
Issue. 2,
p.
525.
Chifan, Ionut
and
Houdayer, Cyril
2010.
Bass-Serre rigidity results in von Neumann algebras.
Duke Mathematical Journal,
Vol. 153,
Issue. 1,
Gaboriau, Damien
2011.
Free product actions with relative property (T) and trivial outer automorphism groups.
Journal of Functional Analysis,
Vol. 260,
Issue. 2,
p.
414.
Ioana, Adrian
2011.
Orbit inequivalent actions for groups containing a copy of $\mathbb{F}_{2}$.
Inventiones mathematicae,
Vol. 185,
Issue. 1,
p.
55.
Törnquist, Asger
2011.
Localized cohomology and some applications of Popa’s cocycle superrigidity theorem.
Israel Journal of Mathematics,
Vol. 181,
Issue. 1,
p.
327.
Conley, Clinton
and
Miller, Benjamin
2014.
An antibasis result for graphs of infinite Borel chromatic number.
Proceedings of the American Mathematical Society,
Vol. 142,
Issue. 6,
p.
2123.
Carderi, Alessandro
and
Le Maître, François
2016.
More Polish full groups.
Topology and its Applications,
Vol. 202,
Issue. ,
p.
80.
CONLEY, CLINTON T.
and
MILLER, BENJAMIN D.
2017.
Incomparable actions of free groups.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 7,
p.
2084.
Moroz, Inessa
and
Törnquist, Asger
2021.
The Borel complexity of von Neumann equivalence.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 5,
p.
102913.