Article contents
Ordinal definability in Jensen's model
Published online by Cambridge University Press: 12 March 2014
Extract
In [J] R. Jensen proved that any model of ZFC can be generically extended to a model of ZFC + (∃a ⊆ ω)(V = L[a]). This extension was made via a class P of forcing conditions. One can ask what can be said about the class HOD in such extensions. In particular one can ask whether V = HOD holds in Jensen's model. A full answer to this question is given by the following assertion:
Theorem. Let N = L[a] be given by forcing with Jensen's conditions (the classP).
Then:
1. N ⊨ V ≠ HOD,
2. N ⊨ (∀n < ω)(HODn + 1 ⊈ HODω).
3. N ⊨ (∀α ≥ ω)(HODα = HODω), or equivalently HODω + 1 = HODω.
The result is established by investigating homogeneity properties of certain complete Boolean algebras that are associated with the partial orderings of forcing conditions for coding using almost disjoint sets.
We explain shortly the first of our two technical results: It is rather well known that if we have a subset 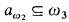 then by performing threefold almost disjoint coding we come to a set a0 ⊆ ω such that
then by performing threefold almost disjoint coding we come to a set a0 ⊆ ω such that 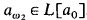 ; cf. [JS]. This is achieved by iterating over
; cf. [JS]. This is achieved by iterating over 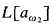 almost disjoint forcing
almost disjoint forcing 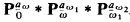 . That means we first code
. That means we first code 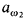 by a subset
by a subset 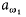 , of [ω1ω2) using the almost disjoint forcing conditions
, of [ω1ω2) using the almost disjoint forcing conditions 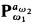 . Then we code
. Then we code 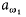 by aω, contained in [ω, ω1), using forcing with
by aω, contained in [ω, ω1), using forcing with 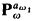 over
over 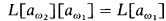 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 1
- Cited by

