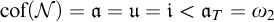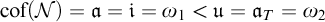1 Introduction
One of the oldest questions regarding the theory of cardinal invariants of the continuum is the following question of Vaughan [Reference Vaughan50]: Is the inequality
![]() $\mathfrak {i}<\mathfrak {a}$
consistent?Footnote
1
The problem involves two fundamental objects in infinite combinatorics (maximal independent families and MAD families) and moreover, a positive answer will most likely require the development of new ideas and forcing techniques.Footnote
2
In order to gain more insight into the above question, we compare
$\mathfrak {i}<\mathfrak {a}$
consistent?Footnote
1
The problem involves two fundamental objects in infinite combinatorics (maximal independent families and MAD families) and moreover, a positive answer will most likely require the development of new ideas and forcing techniques.Footnote
2
In order to gain more insight into the above question, we compare
![]() $\mathfrak {i}$
with the following cardinal invariant introduced by Miller in [Reference Miller, Barwise, Keisler and Kunen40].
$\mathfrak {i}$
with the following cardinal invariant introduced by Miller in [Reference Miller, Barwise, Keisler and Kunen40].
Definition. Define
![]() $\mathfrak {a}_{T}$
as the smallest size of a partition of
$\mathfrak {a}_{T}$
as the smallest size of a partition of
![]() $\omega ^{\omega }$
into compact sets.
$\omega ^{\omega }$
into compact sets.
It is well-known that the Baire space
![]() $\omega ^{\omega }$
is not
$\omega ^{\omega }$
is not
![]() $\sigma $
-compact (see [Reference Kechris32]), which implies that
$\sigma $
-compact (see [Reference Kechris32]), which implies that
![]() $\mathfrak {a}_{T}$
is uncountable. Furthermore,
$\mathfrak {a}_{T}$
is uncountable. Furthermore,
![]() $\mathfrak {d}$
is the least size of a family of compact sets covering
$\mathfrak {d}$
is the least size of a family of compact sets covering
![]() $\omega ^{\omega }$
(see [Reference Bartoszyński and Judah3]), so it follows that
$\omega ^{\omega }$
(see [Reference Bartoszyński and Judah3]), so it follows that
![]() $\mathfrak {d\leq a}_{T}.$
It is known that the compact subspaces of the Baire space are in correspondence with the finitely branching subtrees of
$\mathfrak {d\leq a}_{T}.$
It is known that the compact subspaces of the Baire space are in correspondence with the finitely branching subtrees of
![]() $\omega ^{<\omega }.$
Using this correspondence and König’s lemma, it is easy to prove that
$\omega ^{<\omega }.$
Using this correspondence and König’s lemma, it is easy to prove that
![]() $\mathfrak {a}_{T}$
is equal to the least size of a maximal AD family of finitely branching subtrees of
$\mathfrak {a}_{T}$
is equal to the least size of a maximal AD family of finitely branching subtrees of
![]() $\omega ^{<\omega }.$
Džamonja, Hrušák, and Moore proved that
$\omega ^{<\omega }.$
Džamonja, Hrušák, and Moore proved that
![]() $\Diamond _{\mathfrak {d}}$
implies that
$\Diamond _{\mathfrak {d}}$
implies that
![]() $\mathfrak {a}_{T}=\omega _{1}$
(see Theorem 7.6 of [Reference Moore, Hrušák and Džamonja43]). Thus, since
$\mathfrak {a}_{T}=\omega _{1}$
(see Theorem 7.6 of [Reference Moore, Hrušák and Džamonja43]). Thus, since
![]() $\Diamond _{\mathfrak {d}}$
holds in most of the natural models of
$\Diamond _{\mathfrak {d}}$
holds in most of the natural models of
![]() $\mathfrak {d}=\omega _{1}$
(see [Reference Hrušák28, Reference Moore, Hrušák and Džamonja43] for a precise formulation of this statement),
$\mathfrak {d}=\omega _{1}$
(see [Reference Hrušák28, Reference Moore, Hrušák and Džamonja43] for a precise formulation of this statement),
![]() $\mathfrak {a}_{T}=\omega _{1}$
also holds in these models.
$\mathfrak {a}_{T}=\omega _{1}$
also holds in these models.
On the other hand, given a partition
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\omega ^{\omega }$
into compact sets, Miller introduced a proper forcing notion
$\omega ^{\omega }$
into compact sets, Miller introduced a proper forcing notion
![]() $\mathbb {Q}(\mathcal {C})$
which has the Laver property and destroys
$\mathbb {Q}(\mathcal {C})$
which has the Laver property and destroys
![]() $\mathcal {C}$
, that is,
$\mathcal {C}$
, that is,
![]() $\mathcal {C}$
no longer covers
$\mathcal {C}$
no longer covers
![]() $\omega ^{\omega }$
after forcing with
$\omega ^{\omega }$
after forcing with
![]() $\mathbb {Q}(\mathcal {C})$
. The forcing notion is known as Miller partition forcing and plays an important role in the current article (see Definition 2.1). Spinas showed that
$\mathbb {Q}(\mathcal {C})$
. The forcing notion is known as Miller partition forcing and plays an important role in the current article (see Definition 2.1). Spinas showed that
![]() $\mathbb {Q}(\mathcal {C})$
is
$\mathbb {Q}(\mathcal {C})$
is
![]() ${{}^{\omega }\omega }$
-bounding, which together with Miller’s result establishes the Sacks property of
${{}^{\omega }\omega }$
-bounding, which together with Miller’s result establishes the Sacks property of
![]() $\mathbb {Q}(\mathcal {C})$
(see [Reference Spinas49]). Thus, every partition of
$\mathbb {Q}(\mathcal {C})$
(see [Reference Spinas49]). Thus, every partition of
![]() $\omega ^{\omega }$
into compact sets can be destroyed with a proper forcing that has the Sacks property, which implies the consistency of
$\omega ^{\omega }$
into compact sets can be destroyed with a proper forcing that has the Sacks property, which implies the consistency of
![]() $cof\left ( \mathcal {N}\right ) <\mathfrak {a}_{T}$
and in particular the consistency of
$cof\left ( \mathcal {N}\right ) <\mathfrak {a}_{T}$
and in particular the consistency of
![]() $\mathfrak {d<a}_{T}$
. In [Reference Zapletal52, Proposition 4.1.31], Zapletal proved that
$\mathfrak {d<a}_{T}$
. In [Reference Zapletal52, Proposition 4.1.31], Zapletal proved that
![]() $\mathbb {Q(\mathcal {C})}$
is forcing equivalent to the quotient of the Borel sets of
$\mathbb {Q(\mathcal {C})}$
is forcing equivalent to the quotient of the Borel sets of
![]() $\omega ^{\omega }$
modulo a
$\omega ^{\omega }$
modulo a
![]() $\sigma $
-ideal generated by closed sets. In this way, the forcing
$\sigma $
-ideal generated by closed sets. In this way, the forcing
![]() $\mathbb {Q(\mathcal {C})}$
falls into the scope of the theory developed in [Reference Zapletal51, Reference Zapletal52].
$\mathbb {Q(\mathcal {C})}$
falls into the scope of the theory developed in [Reference Zapletal51, Reference Zapletal52].
In this article, we study the effect of Miller partition forcing on the independence number
![]() $\mathfrak {i}$
and obtain the consistency of
$\mathfrak {i}$
and obtain the consistency of
![]() $\mathfrak {i}<\mathfrak {a}_T$
. The key argument is the fact that Miller partition forcing preserves selective independent families, a fact for which we provide two proofs: one building on the notion of fusion with witnesses (see Definition 2.5) and one building on Laflamme’s filter games (see [Reference Laflamme34]). Both, the fusion with witnesses and the use of Laflamme’s filter game in the context of Miller’s partition forcing, are highly innovative and do not occur in earlier work on
$\mathfrak {i}<\mathfrak {a}_T$
. The key argument is the fact that Miller partition forcing preserves selective independent families, a fact for which we provide two proofs: one building on the notion of fusion with witnesses (see Definition 2.5) and one building on Laflamme’s filter games (see [Reference Laflamme34]). Both, the fusion with witnesses and the use of Laflamme’s filter game in the context of Miller’s partition forcing, are highly innovative and do not occur in earlier work on
![]() $\mathbb {Q}(\mathcal {C})$
.
$\mathbb {Q}(\mathcal {C})$
.
The notion of selective independent family was introduced by Shelah in his work on the consistency of
![]() $\mathfrak {i<u}$
(see [Reference Shelah46]). Selective independent families are families with very strong combinatorial properties, which resemble the combinatorial features of Ramsey ultrafilters. Studying the similarities and differences between selective independent families and Ramsey ultrafilters remains a very interesting line of research. For more recent work on maximal independent families see [Reference Brendle, Fischer and Khomskii13, Reference Chodounský, Fischer and Grebík14, Reference Fischer and Montoya17, Reference Fischer and Shelah18, Reference Perron45].
$\mathfrak {i<u}$
(see [Reference Shelah46]). Selective independent families are families with very strong combinatorial properties, which resemble the combinatorial features of Ramsey ultrafilters. Studying the similarities and differences between selective independent families and Ramsey ultrafilters remains a very interesting line of research. For more recent work on maximal independent families see [Reference Brendle, Fischer and Khomskii13, Reference Chodounský, Fischer and Grebík14, Reference Fischer and Montoya17, Reference Fischer and Shelah18, Reference Perron45].
Employing our notion of fusion with witnesses, we show also that
![]() $\mathbb {Q}(\mathcal {C})$
preserves P-points. Together with the fact that Miller partition forcing and its iterations preserve tight mad families (see [Reference Guzmán, Hrušák and Téllez25]), we obtain the consistency of the following constellation:
$\mathbb {Q}(\mathcal {C})$
preserves P-points. Together with the fact that Miller partition forcing and its iterations preserve tight mad families (see [Reference Guzmán, Hrušák and Téllez25]), we obtain the consistency of the following constellation:
Theorem. It is relatively consistent that
![]() $\mathfrak {i}=\mathfrak {a}=\mathfrak {u}=\omega _1<\mathfrak {a}_T$
.
$\mathfrak {i}=\mathfrak {a}=\mathfrak {u}=\omega _1<\mathfrak {a}_T$
.
The question if one can increase simultaneously
![]() $\mathfrak {u}$
and
$\mathfrak {u}$
and
![]() $\mathfrak {a}_T$
, while preserving small witnesses to
$\mathfrak {a}_T$
, while preserving small witnesses to
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {i}$
becomes of interest. Further, we show that Shelah’s poset
$\mathfrak {i}$
becomes of interest. Further, we show that Shelah’s poset
![]() $\mathbb {Q}_{\mathcal {I}}$
for destroying the maximality of a given maximal ideal from [Reference Shelah46] strongly preserves tight MAD families. The following result appears as Corollary 5.14 in the current article:
$\mathbb {Q}_{\mathcal {I}}$
for destroying the maximality of a given maximal ideal from [Reference Shelah46] strongly preserves tight MAD families. The following result appears as Corollary 5.14 in the current article:
Theorem. It is relatively consistent that
![]() $\mathfrak {i}=\mathfrak {a}=\omega _1<\mathfrak {u}$
.
$\mathfrak {i}=\mathfrak {a}=\omega _1<\mathfrak {u}$
.
Finally, combining Miller partition forcing, Shelah’s
![]() $\mathbb {Q}_{\mathcal {I}}$
, our preservation results, as well as the preservation results of [Reference Guzmán, Hrušák and Téllez25, Reference Shelah46], in Corollary 5.15 we obtain:
$\mathbb {Q}_{\mathcal {I}}$
, our preservation results, as well as the preservation results of [Reference Guzmán, Hrušák and Téllez25, Reference Shelah46], in Corollary 5.15 we obtain:
Theorem. It is relatively consistent that
![]() $\mathfrak {i}=\mathfrak {a}=\omega _1<\mathfrak {u}=\mathfrak {a}_T=\omega _2$
.
$\mathfrak {i}=\mathfrak {a}=\omega _1<\mathfrak {u}=\mathfrak {a}_T=\omega _2$
.
2 Miller partition forcing
2.1 Fusion with witnesses
Recall that Sacks forcing
![]() $\mathbb {S}$
consists of all perfect trees in
$\mathbb {S}$
consists of all perfect trees in
![]() $2^{<\omega }$
ordered by inclusion. That is,
$2^{<\omega }$
ordered by inclusion. That is,
![]() $p\in \mathbb {S}$
if and only if:
$p\in \mathbb {S}$
if and only if:
-
(1)
 $p\subseteq 2^{<\omega }$
,
$p\subseteq 2^{<\omega }$
, -
(2)
 $\forall \sigma \in p\; \forall \tau \in 2^{<\omega }\big (\tau \subseteq \sigma \rightarrow \tau \in p\big ),$
$\forall \sigma \in p\; \forall \tau \in 2^{<\omega }\big (\tau \subseteq \sigma \rightarrow \tau \in p\big ),$
-
(3)
 $\forall \sigma \in p\; \exists \tau , \tau '\in p\big ( \sigma \subseteq \tau \wedge \sigma \subseteq \tau ' \wedge \tau \not \subseteq \tau '\wedge \tau '\not \subseteq \tau \big )$
.
$\forall \sigma \in p\; \exists \tau , \tau '\in p\big ( \sigma \subseteq \tau \wedge \sigma \subseteq \tau ' \wedge \tau \not \subseteq \tau '\wedge \tau '\not \subseteq \tau \big )$
.
We will use standard notation: If
![]() $p\in \mathbb {S}$
and
$p\in \mathbb {S}$
and
![]() $\sigma \in p$
we let
$\sigma \in p$
we let
![]() $p(\sigma )=\{\tau \in p\;|\; \tau \subseteq \sigma \text { or } \sigma \subseteq \tau \}$
and call
$p(\sigma )=\{\tau \in p\;|\; \tau \subseteq \sigma \text { or } \sigma \subseteq \tau \}$
and call
![]() $\sigma $
a splitting node if
$\sigma $
a splitting node if
![]() $\sigma ^{\smallfrown } i\in p $
for each
$\sigma ^{\smallfrown } i\in p $
for each
![]() $i\in 2$
. Let
$i\in 2$
. Let
![]() $split(p)=\{\sigma \in p\;|\; \sigma \text { is a splitting node }\}$
. For each
$split(p)=\{\sigma \in p\;|\; \sigma \text { is a splitting node }\}$
. For each
![]() $n\in \omega $
let
$n\in \omega $
let
![]() $split_n(p)=\{\sigma \in split(p)\;|\; |\{\tau \in split(p) \;| \; \tau \subsetneq \sigma \}|=n\}$
and
$split_n(p)=\{\sigma \in split(p)\;|\; |\{\tau \in split(p) \;| \; \tau \subsetneq \sigma \}|=n\}$
and
![]() $stem(p)$
the unique element in
$stem(p)$
the unique element in
![]() $split_0(p)$
. Finally, for
$split_0(p)$
. Finally, for
![]() $p\in \mathbb {S}$
let
$p\in \mathbb {S}$
let
![]() $[p]=\{f\in 2^{\omega } \;|\; \forall n\in \omega (\;f|_n\in p \;)\}.$
More about Sacks forcing can be found in [Reference Baumgartner4, Reference Baumgartner and Laver5, Reference Fernández-Bretón and Hrušák15, Reference Geschke and Quickert23, Reference Hrušák29, Reference Miller42, Reference Zheng53].
$[p]=\{f\in 2^{\omega } \;|\; \forall n\in \omega (\;f|_n\in p \;)\}.$
More about Sacks forcing can be found in [Reference Baumgartner4, Reference Baumgartner and Laver5, Reference Fernández-Bretón and Hrušák15, Reference Geschke and Quickert23, Reference Hrušák29, Reference Miller42, Reference Zheng53].
Definition 2.1 (Miller partition forcing).
Let
![]() $\mathcal {C}\subseteq \mathcal {P}(2^{\omega })$
be an uncountable partition of
$\mathcal {C}\subseteq \mathcal {P}(2^{\omega })$
be an uncountable partition of
![]() $2^{\omega }$
into closed sets and let
$2^{\omega }$
into closed sets and let
ordered by reversed inclusion.
This forcing destroys the partition
![]() $\mathcal {C}$
in the following way. If G is a
$\mathcal {C}$
in the following way. If G is a
![]() $\mathbb {Q}(\mathcal {C})$
-generic filter, then
$\mathbb {Q}(\mathcal {C})$
-generic filter, then
is an element of
![]() $2^{\omega }$
which does not belong to the interpretation in
$2^{\omega }$
which does not belong to the interpretation in
![]() $V[G]$
of any element of
$V[G]$
of any element of
![]() $\mathcal {C}$
. So in
$\mathcal {C}$
. So in
![]() $V[G]$
,
$V[G]$
,
![]() $\mathcal {C}$
is no longer a partition of
$\mathcal {C}$
is no longer a partition of
![]() $2^{\omega }$
. Thus, if we start with a model of CH and define
$2^{\omega }$
. Thus, if we start with a model of CH and define
![]() $\mathbb {PM}$
as the resulting model after forcing with a countable support iteration of length
$\mathbb {PM}$
as the resulting model after forcing with a countable support iteration of length
![]() $\omega _2$
of all forcing notions of the form
$\omega _2$
of all forcing notions of the form
![]() $\mathbb {Q}(\mathcal {C})$
with
$\mathbb {Q}(\mathcal {C})$
with
![]() $\mathcal {C}$
ranging over all uncountable partitions in closed sets of
$\mathcal {C}$
ranging over all uncountable partitions in closed sets of
![]() $2^{\omega }$
in all intermediate models, then
$2^{\omega }$
in all intermediate models, then
![]() $\mathbb {PM}$
will not have any uncountable partition in closed sets of
$\mathbb {PM}$
will not have any uncountable partition in closed sets of
![]() $2^{\omega }$
of size less than
$2^{\omega }$
of size less than
![]() $\omega _2$
. Note that, Miller defined and used
$\omega _2$
. Note that, Miller defined and used
![]() $\mathbb {PM}$
in [Reference Miller, Barwise, Keisler and Kunen40] to show that
$\mathbb {PM}$
in [Reference Miller, Barwise, Keisler and Kunen40] to show that
![]() $cov(\mathcal {M})=\omega _1$
does not imply that
$cov(\mathcal {M})=\omega _1$
does not imply that
![]() $\mathfrak {a}_T=\omega _1$
.
$\mathfrak {a}_T=\omega _1$
.
Notice that if
![]() $\mathcal {C}$
is the partition of
$\mathcal {C}$
is the partition of
![]() $2^{\omega }$
into singletons, then
$2^{\omega }$
into singletons, then
![]() $\mathbb {Q}(\mathcal {C})=\mathbb {S}$
. Actually, it can be seen that if
$\mathbb {Q}(\mathcal {C})=\mathbb {S}$
. Actually, it can be seen that if
![]() $\mathcal {C}$
is an analytic subset of
$\mathcal {C}$
is an analytic subset of
![]() $K(2^{\omega })$
, where
$K(2^{\omega })$
, where
![]() $K(2^{\omega })$
is the space of non-empty closed subsets of
$K(2^{\omega })$
is the space of non-empty closed subsets of
![]() $2^{\omega }$
equipped with the Vietoris topology, then
$2^{\omega }$
equipped with the Vietoris topology, then
![]() $\mathbb {Q}(\mathcal {C})$
is forcing equivalent to Sacks forcing
$\mathbb {Q}(\mathcal {C})$
is forcing equivalent to Sacks forcing
![]() $\mathbb {S}$
.
$\mathbb {S}$
.
Theorem 2.2. Let
![]() $\mathcal {C}\subseteq K(2^{\omega }) $
be an uncountable analytic partition of
$\mathcal {C}\subseteq K(2^{\omega }) $
be an uncountable analytic partition of
![]() $2^{\omega }$
. Then
$2^{\omega }$
. Then
![]() $\mathbb {Q}(\mathcal {C})$
is forcing equivalent to Sacks forcing
$\mathbb {Q}(\mathcal {C})$
is forcing equivalent to Sacks forcing
![]() $\mathbb {S}$
.
$\mathbb {S}$
.
Proof Let
![]() $p\in \mathbb {Q}(\mathcal {C})$
. It is enough to find
$p\in \mathbb {Q}(\mathcal {C})$
. It is enough to find
![]() $q\in \mathbb {Q}(\mathcal {C})$
such that
$q\in \mathbb {Q}(\mathcal {C})$
such that
![]() $q\leq p$
and
$q\leq p$
and
![]() $\{r\in \mathbb {Q}(\mathcal {C})\;|\; r\leq q\}=\{r\in \mathbb {S}\;|\;r\subseteq q\}.$
To do this consider continuous
$\{r\in \mathbb {Q}(\mathcal {C})\;|\; r\leq q\}=\{r\in \mathbb {S}\;|\;r\subseteq q\}.$
To do this consider continuous
![]() $f:K(2^{\omega })\longrightarrow 2^{\omega }$
given by
$f:K(2^{\omega })\longrightarrow 2^{\omega }$
given by
![]() $f(A)=min A$
and let
$f(A)=min A$
and let
![]() $X=\{ K\cap [p]\;| \; K\in \mathcal {C}\}\backslash \{\emptyset \}$
. Notice that X is an uncountable analytic subset of
$X=\{ K\cap [p]\;| \; K\in \mathcal {C}\}\backslash \{\emptyset \}$
. Notice that X is an uncountable analytic subset of
![]() $K(2^{\omega })$
,
$K(2^{\omega })$
,
![]() $f|_X$
is injective, and
$f|_X$
is injective, and
![]() $im(f|_X)\subseteq [p]$
. This implies that there is
$im(f|_X)\subseteq [p]$
. This implies that there is
![]() $q\in \mathbb {S}$
such that
$q\in \mathbb {S}$
such that
![]() $[q]\subseteq im(f|_X)$
. It is easy to see that
$[q]\subseteq im(f|_X)$
. It is easy to see that
![]() $q\subseteq p$
and
$q\subseteq p$
and
![]() $|[q]\cap K|\leq 1$
for every
$|[q]\cap K|\leq 1$
for every
![]() $K\in \mathcal {C}$
. Checking that q is as desired is straightforward.
$K\in \mathcal {C}$
. Checking that q is as desired is straightforward.
A main difficulty in adapting Sacks fusion sequences to
![]() $\mathbb {Q}(\mathcal {C})$
is guaranteeing that the fusion is indeed an element of
$\mathbb {Q}(\mathcal {C})$
is guaranteeing that the fusion is indeed an element of
![]() $\mathbb {Q}(\mathcal {C})$
. To have a better control over fusion sequences in
$\mathbb {Q}(\mathcal {C})$
. To have a better control over fusion sequences in
![]() $\mathbb {Q}(\mathcal {C})$
we introduce the notion of a fusion with witnesses (see Definition 2.5). We begin with some auxiliary notions.
$\mathbb {Q}(\mathcal {C})$
we introduce the notion of a fusion with witnesses (see Definition 2.5). We begin with some auxiliary notions.
Definition 2.3. Let
![]() $\mathcal {C}=\{C_{\alpha }\}_{\alpha \in \omega _1}$
be an uncountable partition of
$\mathcal {C}=\{C_{\alpha }\}_{\alpha \in \omega _1}$
be an uncountable partition of
![]() $2^{\omega }$
into closed sets.
$2^{\omega }$
into closed sets.
-
(1) We say that
 $x,y\in {}^{\omega }2$
are
$x,y\in {}^{\omega }2$
are
 $\mathcal {C}$
-different if
$\mathcal {C}$
-different if
 $x,y$
belong to different elements of
$x,y$
belong to different elements of
 $\mathcal {C}$
.
$\mathcal {C}$
. -
(2) A tree
 $p\subseteq 2^{<\omega }$
is said to be
$p\subseteq 2^{<\omega }$
is said to be
 $\mathcal {C}$
-branching if for any
$\mathcal {C}$
-branching if for any
 $s\in p$
there are
$s\in p$
there are
 $\mathcal {C}$
-different branches in
$\mathcal {C}$
-different branches in
 $[p]$
extending s.
$[p]$
extending s.
Note that, a
![]() $\mathcal {C}$
-branching tree is perfect. We will use the following notation: whenever
$\mathcal {C}$
-branching tree is perfect. We will use the following notation: whenever
![]() $\mathcal {C}$
as above is given, for each
$\mathcal {C}$
as above is given, for each
![]() $x\in 2^{\omega }$
we denote by
$x\in 2^{\omega }$
we denote by
![]() $\alpha _x$
the unique ordinal such that
$\alpha _x$
the unique ordinal such that
![]() $x\in C_{\alpha _x}$
.
$x\in C_{\alpha _x}$
.
The equivalence of
![]() $(a)$
and
$(a)$
and
![]() $(c)$
in the lemma below can be found in [Reference Guzmán, Hrušák and Téllez25].
$(c)$
in the lemma below can be found in [Reference Guzmán, Hrušák and Téllez25].
Lemma 2.4. Let
![]() $p\subseteq 2^{<\omega }$
be a tree. The following are equivalent:
$p\subseteq 2^{<\omega }$
be a tree. The following are equivalent:
-
(a)
 $p\in \mathbb {Q}(\mathcal {C})$
.
$p\in \mathbb {Q}(\mathcal {C})$
. -
(b) p is
 $\mathcal {C}$
-branching.
$\mathcal {C}$
-branching. -
(c) p is perfect and
 $[p]$
contains a countable dense subset with
$[p]$
contains a countable dense subset with
 $\mathcal {C}$
-different branches.
$\mathcal {C}$
-different branches.
Proof
![]() $(\mathrm {(a)}\Rightarrow \mathrm {(c)})$
Let
$(\mathrm {(a)}\Rightarrow \mathrm {(c)})$
Let
![]() $p\in \mathbb {Q}(\mathcal {C})$
. p is a perfect tree by the definition. Thus arrange
$p\in \mathbb {Q}(\mathcal {C})$
. p is a perfect tree by the definition. Thus arrange
![]() $\operatorname {\mathrm {split}}(p)$
and assign by induction to each splitting node s a real x from
$\operatorname {\mathrm {split}}(p)$
and assign by induction to each splitting node s a real x from
![]() $[p]$
extending s which was either already considered or belongs to a different set from
$[p]$
extending s which was either already considered or belongs to a different set from
![]() $\mathcal {C}$
than all previously selected reals. This is possible since any
$\mathcal {C}$
than all previously selected reals. This is possible since any
![]() $s\in \operatorname {\mathrm {split}}(p)$
may be extended to
$s\in \operatorname {\mathrm {split}}(p)$
may be extended to
![]() $t\in \operatorname {\mathrm {split}}(p)$
with
$t\in \operatorname {\mathrm {split}}(p)$
with
![]() $[p(t)]$
being disjoint with finitely many sets from
$[p(t)]$
being disjoint with finitely many sets from
![]() $\mathcal {C}$
containing all previously selected reals. The set of all assigned branches is the required dense set.
$\mathcal {C}$
containing all previously selected reals. The set of all assigned branches is the required dense set.
![]() $(\mathrm {(c)}\Rightarrow \mathrm {(b)})$
Trivial.
$(\mathrm {(c)}\Rightarrow \mathrm {(b)})$
Trivial.
![]() $(\mathrm {(b)}\Rightarrow \mathrm {(a)})$
Let
$(\mathrm {(b)}\Rightarrow \mathrm {(a)})$
Let
![]() $\beta <\omega _1$
and
$\beta <\omega _1$
and
![]() $s\in p$
. There are
$s\in p$
. There are
![]() $x,y\in [p]$
such that
$x,y\in [p]$
such that
![]() $s\subseteq x,y$
and
$s\subseteq x,y$
and
![]() $\alpha _x\neq \alpha _y$
. We take
$\alpha _x\neq \alpha _y$
. We take
![]() $z\in \{x,y\}$
such that
$z\in \{x,y\}$
such that
![]() $\alpha _z\neq \beta $
. Since
$\alpha _z\neq \beta $
. Since
![]() $z\in [p]\setminus C_{\beta }$
and
$z\in [p]\setminus C_{\beta }$
and
![]() $C_{\beta }$
is closed, there is
$C_{\beta }$
is closed, there is
![]() $s\subseteq t\subseteq z$
such that
$s\subseteq t\subseteq z$
such that
![]() $[p(t)]\cap C_{\beta }=\emptyset $
.
$[p(t)]\cap C_{\beta }=\emptyset $
.
The particular enumeration constructed in Lemma 2.4 will be applied several times. Therefore we state explicitly that we may assume the dense set in Lemma 2.4 is enumerated as
![]() $\{x_t\colon t\in p\}$
such that
$\{x_t\colon t\in p\}$
such that
![]() $s\subseteq x_s$
, and if
$s\subseteq x_s$
, and if
![]() $s\subseteq t\subseteq x_s$
then
$s\subseteq t\subseteq x_s$
then
![]() $x_t=x_s$
.
$x_t=x_s$
.
Definition 2.5 (Fusion sequence with witnesses).
-
(1) Let p be a condition in
 $\mathbb {Q}(\mathcal {C})$
. We say that a set
$\mathbb {Q}(\mathcal {C})$
. We say that a set
 $X\subseteq {}^{\omega }2$
is a p-witness for the n-th level if
$X\subseteq {}^{\omega }2$
is a p-witness for the n-th level if
 $X\subseteq [p]$
, for each
$X\subseteq [p]$
, for each
 $s\in \operatorname {\mathrm {split}}_n(p)$
there is
$s\in \operatorname {\mathrm {split}}_n(p)$
there is
 $x\in X$
extending s, and X has
$x\in X$
extending s, and X has
 $\mathcal {C}$
-different elements. Note that if X is a p-witness for the
$\mathcal {C}$
-different elements. Note that if X is a p-witness for the
 $(n+1)$
-st level then each node from the n-th splitting level of p is contained in
$(n+1)$
-st level then each node from the n-th splitting level of p is contained in
 $\mathcal {C}$
-different branches in X.
$\mathcal {C}$
-different branches in X. -
(2) Let
 $(p,X),(q,Y)$
be pairs with
$(p,X),(q,Y)$
be pairs with
 $p,q$
conditions in
$p,q$
conditions in
 $\mathbb {Q}(\mathcal {C})$
. Let X be a p-witness for the
$\mathbb {Q}(\mathcal {C})$
. Let X be a p-witness for the
 $(n+1)$
-st level and let Y be a q-witness for the n-th level. Then Note that if
$(n+1)$
-st level and let Y be a q-witness for the n-th level. Then Note that if $$ \begin{align*} (p,X)\leq^n(q,Y) \ \mathrm{if \ and \ only \ if} \ p\leq q \ \mathrm{and} \ X\supseteq Y. \end{align*} $$
$$ \begin{align*} (p,X)\leq^n(q,Y) \ \mathrm{if \ and \ only \ if} \ p\leq q \ \mathrm{and} \ X\supseteq Y. \end{align*} $$
 $(p,X)\leq ^n(q,Y)$
then
$(p,X)\leq ^n(q,Y)$
then
 $\operatorname {\mathrm {split}}_{<n}(p)=\operatorname {\mathrm {split}}_{<n}(q)$
.
$\operatorname {\mathrm {split}}_{<n}(p)=\operatorname {\mathrm {split}}_{<n}(q)$
.
-
(3) A sequence
 $\{(p_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses if
$\{(p_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses if
 $(p_{n+1},X_{n+1})\leq ^n(p_n,X_n)$
for each n.
$(p_{n+1},X_{n+1})\leq ^n(p_n,X_n)$
for each n.
Lemma 2.6. If a sequence
![]() $\{(p_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses then the fusion
$\{(p_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses then the fusion
![]() $\bigcap \{p_n: n\in \omega \}$
is a condition in
$\bigcap \{p_n: n\in \omega \}$
is a condition in
![]() $\mathbb {Q}(\mathcal {C})$
.
$\mathbb {Q}(\mathcal {C})$
.
Proof We denote
![]() $p=\bigcap \{p_n\colon n\in \omega \}$
,
$p=\bigcap \{p_n\colon n\in \omega \}$
,
![]() $X=\bigcup \{X_n: n\in \omega \}$
, and we assume that we have
$X=\bigcup \{X_n: n\in \omega \}$
, and we assume that we have
![]() $s\in p$
. We take
$s\in p$
. We take
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $t\in \operatorname {\mathrm {split}}_n(p)$
such that t extends s. Since
$t\in \operatorname {\mathrm {split}}_n(p)$
such that t extends s. Since
![]() $\operatorname {\mathrm {split}}_n(p)=\operatorname {\mathrm {split}}_n(p_{n+1})$
, the set
$\operatorname {\mathrm {split}}_n(p)=\operatorname {\mathrm {split}}_n(p_{n+1})$
, the set
![]() $X_{n+1}$
contains
$X_{n+1}$
contains
![]() $\mathcal {C}$
-different branches extending t. Hence, X is dense in
$\mathcal {C}$
-different branches extending t. Hence, X is dense in
![]() $[p]$
. One can easily see that X is contained in
$[p]$
. One can easily see that X is contained in
![]() $[p]$
. Finally, by Lemma 2.4 we conclude that
$[p]$
. Finally, by Lemma 2.4 we conclude that
![]() $p\in \mathbb {Q}(\mathcal {C})$
.
$p\in \mathbb {Q}(\mathcal {C})$
.
Miller [Reference Miller, Barwise, Keisler and Kunen40] and Spinas [Reference Spinas49] applied separate fusion arguments in their proofs, while Miller [Reference Miller, Barwise, Keisler and Kunen40] introduced the notion of a fusion even formally. The partial order
![]() $\mathbb {Q}(\mathcal {C})$
was recently used in [Reference Guzmán, Hrušák and Téllez25], where the notion of a nice sequence was isolated from Spinas’s fusion arguments. Our definition of fusion sequence covers both approaches. The sequence
$\mathbb {Q}(\mathcal {C})$
was recently used in [Reference Guzmán, Hrušák and Téllez25], where the notion of a nice sequence was isolated from Spinas’s fusion arguments. Our definition of fusion sequence covers both approaches. The sequence
![]() $\{X_n\}_{n\in \omega }$
in our definition may be obtained as sets of leftmost branches in Miller’s fusion argument, and as certain terms of nice sequence in Spinas’s approach.
$\{X_n\}_{n\in \omega }$
in our definition may be obtained as sets of leftmost branches in Miller’s fusion argument, and as certain terms of nice sequence in Spinas’s approach.
In addition to fusion sequences, we shall use two basic schemas to amalgamate conditions. Let us have a condition
![]() $p\in \mathbb {Q}(\mathcal {C})$
, and for each
$p\in \mathbb {Q}(\mathcal {C})$
, and for each
![]() $s\in \operatorname {\mathrm {split}}_n(p)$
,
$s\in \operatorname {\mathrm {split}}_n(p)$
,
![]() $i\in \{0,1\}$
, a condition
$i\in \{0,1\}$
, a condition
![]() $q(s,i)$
extending
$q(s,i)$
extending
![]() $p(s^{\smallfrown } i)$
. Using Lemma 2.4, one can easily see that the tree
$p(s^{\smallfrown } i)$
. Using Lemma 2.4, one can easily see that the tree
is a condition in
![]() $\mathbb {Q}(\mathcal {C})$
as well. In the second amalgamation technique, we are given a decreasing sequence
$\mathbb {Q}(\mathcal {C})$
as well. In the second amalgamation technique, we are given a decreasing sequence
![]() $\{q_i\}_{i\in \omega }$
of extensions of p with strictly increasing stems
$\{q_i\}_{i\in \omega }$
of extensions of p with strictly increasing stems
![]() $s_n=\operatorname {\mathrm {stem}} q_n$
. We set
$s_n=\operatorname {\mathrm {stem}} q_n$
. We set
![]() $x=\bigcup _{i\in \omega }s_i$
and take
$x=\bigcup _{i\in \omega }s_i$
and take
![]() $q=\bigcup _{i\in \omega }q_i(s_i^{\smallfrown } \langle 1-x(|s_i|)\rangle )$
. Again, using Lemma 2.4, one can easily see that q is a condition in
$q=\bigcup _{i\in \omega }q_i(s_i^{\smallfrown } \langle 1-x(|s_i|)\rangle )$
. Again, using Lemma 2.4, one can easily see that q is a condition in
![]() $\mathbb {Q}(\mathcal {C})$
.
$\mathbb {Q}(\mathcal {C})$
.
The proof of the fact that
![]() $\mathbb {Q}(\mathcal {C})$
is
$\mathbb {Q}(\mathcal {C})$
is
![]() $^{\omega }\omega $
-bounding is underlying many fusion arguments associated with
$^{\omega }\omega $
-bounding is underlying many fusion arguments associated with
![]() $\mathbb {Q}(\mathcal {C})$
. For convenience of the reader, we repeat it here. We will make use of the following two lemmas.
$\mathbb {Q}(\mathcal {C})$
. For convenience of the reader, we repeat it here. We will make use of the following two lemmas.
Lemma 2.7. Let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbb {Q}(\mathcal {C})$
-name for a function in
$\mathbb {Q}(\mathcal {C})$
-name for a function in
![]() $^{\omega }\omega $
and let h be a function in
$^{\omega }\omega $
and let h be a function in
![]() ${}^{\omega }\omega \cap V$
. The set of all conditions q satisfying the following property is dense in
${}^{\omega }\omega \cap V$
. The set of all conditions q satisfying the following property is dense in
![]() $\mathbb {Q}(\mathcal {C})$
: There is a real
$\mathbb {Q}(\mathcal {C})$
: There is a real
![]() $x\in [q]$
and a sequence
$x\in [q]$
and a sequence
![]() $\{f_s\}_{s\in x\restriction \operatorname {\mathrm {split}}(q)}$
of functions in
$\{f_s\}_{s\in x\restriction \operatorname {\mathrm {split}}(q)}$
of functions in
![]() ${}^{<\omega }\omega $
such that for any
${}^{<\omega }\omega $
such that for any
![]() $s=x\restriction \operatorname {\mathrm {split}}_n(q)$
we have
$s=x\restriction \operatorname {\mathrm {split}}_n(q)$
we have
![]() $q(s)\Vdash \dot {f}\upharpoonright h(n)=f_s$
.
$q(s)\Vdash \dot {f}\upharpoonright h(n)=f_s$
.
Proof Let
![]() $p\in \mathbb {Q}(\mathcal {C})$
. One can construct a decreasing sequence
$p\in \mathbb {Q}(\mathcal {C})$
. One can construct a decreasing sequence
![]() $\{q_i\}_{i\in \omega }$
of extensions of p with strictly increasing stems such that
$\{q_i\}_{i\in \omega }$
of extensions of p with strictly increasing stems such that
![]() $q_n\Vdash \dot {f}\upharpoonright h(n)=f_n$
for some
$q_n\Vdash \dot {f}\upharpoonright h(n)=f_n$
for some
![]() $f_n\in {}^{h(n)}\omega $
. We denote
$f_n\in {}^{h(n)}\omega $
. We denote
![]() $s_n=\operatorname {\mathrm {stem}}(q_n)$
and we set
$s_n=\operatorname {\mathrm {stem}}(q_n)$
and we set
![]() $x=\bigcup _{i\in \omega }s_i$
. Finally, we take the amalgamation
$x=\bigcup _{i\in \omega }s_i$
. Finally, we take the amalgamation
![]() $q=\bigcup _{i\in \omega }q_i(s_i^{\smallfrown } \langle 1-x(|s_i|)\rangle )$
.
$q=\bigcup _{i\in \omega }q_i(s_i^{\smallfrown } \langle 1-x(|s_i|)\rangle )$
.
Lemma 2.8. Let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbb {Q}(\mathcal {C})$
-name for a function in
$\mathbb {Q}(\mathcal {C})$
-name for a function in
![]() $^{\omega }\omega $
. The set of all conditions q satisfying the following property is dense in
$^{\omega }\omega $
. The set of all conditions q satisfying the following property is dense in
![]() $\mathbb {Q}(\mathcal {C})$
: For all
$\mathbb {Q}(\mathcal {C})$
: For all
![]() $m\in \omega $
, for all
$m\in \omega $
, for all
![]() $t\in \mbox {split}_m(q)$
there is
$t\in \mbox {split}_m(q)$
there is
![]() $f_t\in {^{m+1}\omega }$
such that
$f_t\in {^{m+1}\omega }$
such that
Proof Let
![]() $p\in \mathbb {Q}(\mathcal {C})$
. We build a fusion sequence
$p\in \mathbb {Q}(\mathcal {C})$
. We build a fusion sequence
![]() $\{(q_n,X_n)\}_{n\in \omega }$
with
$\{(q_n,X_n)\}_{n\in \omega }$
with
![]() $q_0\leq p$
such that its fusion q has the required property. Let the condition
$q_0\leq p$
such that its fusion q has the required property. Let the condition
![]() $q_0$
, branch x, and sequence
$q_0$
, branch x, and sequence
![]() $\{f_s\}_{s\in x\restriction \operatorname {\mathrm {split}}(q_0)}$
be obtained from Lemma 2.7 for p and
$\{f_s\}_{s\in x\restriction \operatorname {\mathrm {split}}(q_0)}$
be obtained from Lemma 2.7 for p and
![]() $h(n)=n+1$
. We set
$h(n)=n+1$
. We set
![]() $X_0=\{x\}$
.
$X_0=\{x\}$
.
Let
![]() $0\leq n<\omega $
. Suppose we have defined
$0\leq n<\omega $
. Suppose we have defined
![]() $q_n\in \mathbb {Q}(\mathcal {C})$
and finite
$q_n\in \mathbb {Q}(\mathcal {C})$
and finite
![]() $X_n\subseteq [q_n]$
. Let
$X_n\subseteq [q_n]$
. Let
![]() $s\in \operatorname {\mathrm {split}}_n(q_n)$
. Take the unique branch
$s\in \operatorname {\mathrm {split}}_n(q_n)$
. Take the unique branch
![]() $x\in X_n$
extending s, node
$x\in X_n$
extending s, node
![]() $r=x\restriction \operatorname {\mathrm {split}}_{n+1}(q_n)$
, and number
$r=x\restriction \operatorname {\mathrm {split}}_{n+1}(q_n)$
, and number
![]() $i=x(|s|)$
in
$i=x(|s|)$
in
![]() $\{0,1\}$
. We set
$\{0,1\}$
. We set
![]() $q(s,i)=q_n(r)$
. Let
$q(s,i)=q_n(r)$
. Let
![]() $t\supseteq s^{\smallfrown } \langle 1-i\rangle $
be such that
$t\supseteq s^{\smallfrown } \langle 1-i\rangle $
be such that
![]() $[q_n(t)]\cap C_{\alpha _x}=\emptyset $
for all already considered branches x (i.e., all branches in
$[q_n(t)]\cap C_{\alpha _x}=\emptyset $
for all already considered branches x (i.e., all branches in
![]() $X_n$
and those assigned to previous nodes in some order of
$X_n$
and those assigned to previous nodes in some order of
![]() $\operatorname {\mathrm {split}}_n(q_n)$
). Use Lemma 2.7 for
$\operatorname {\mathrm {split}}_n(q_n)$
). Use Lemma 2.7 for
![]() $q_n(t)$
and
$q_n(t)$
and
![]() $h(j)=n+j+2$
to obtain
$h(j)=n+j+2$
to obtain
![]() $q(s,1-i)\leq q_n(t)$
, branch x, and sequence
$q(s,1-i)\leq q_n(t)$
, branch x, and sequence
![]() $\{f_s\}_{s\in x\restriction \operatorname {\mathrm {split}}(q_n)}$
.
$\{f_s\}_{s\in x\restriction \operatorname {\mathrm {split}}(q_n)}$
.
Finally, let
![]() $X_{n+1}$
be the set of all considered branches in this step, and
$X_{n+1}$
be the set of all considered branches in this step, and
One can verify that the sequence
![]() $\{(q_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses.
$\{(q_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses.
As an application, we obtain a straightforward proof of the fact that
![]() $\mathbb {Q}(\mathcal {C})$
is
$\mathbb {Q}(\mathcal {C})$
is
![]() $^{\omega }\omega $
-bounding. Since the poset has the Laver property (see [Reference Miller, Barwise, Keisler and Kunen40]), this also gives the Sacks property of
$^{\omega }\omega $
-bounding. Since the poset has the Laver property (see [Reference Miller, Barwise, Keisler and Kunen40]), this also gives the Sacks property of
![]() $\mathbb {Q}(\mathcal {C})$
.
$\mathbb {Q}(\mathcal {C})$
.
Lemma 2.9 (Spinas [Reference Spinas49]).
The poset
![]() $\mathbb {Q}(\mathcal {C})$
has the Sacks property.
$\mathbb {Q}(\mathcal {C})$
has the Sacks property.
Proof As explained above, by Miller’s result it is sufficient to show that
![]() $\mathbb {Q}(\mathcal {C})$
is
$\mathbb {Q}(\mathcal {C})$
is
![]() $^{\omega }\omega $
-bounding. Let
$^{\omega }\omega $
-bounding. Let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbb {Q}(\mathcal {C})$
-name for a function in
$\mathbb {Q}(\mathcal {C})$
-name for a function in
![]() $^{\omega }\omega $
and let
$^{\omega }\omega $
and let
![]() $p\in \mathbb {Q}(\mathcal {C})$
. We will show that there is
$p\in \mathbb {Q}(\mathcal {C})$
. We will show that there is
![]() $q\leq p$
and
$q\leq p$
and
![]() $g\in V\cap {{}^{\omega }\omega }$
such that
$g\in V\cap {{}^{\omega }\omega }$
such that
![]() $q\Vdash \dot {f}\leq ^* \check {g}$
.
$q\Vdash \dot {f}\leq ^* \check {g}$
.
By Lemma 2.8 we can assume that there is
![]() $q\leq p$
such that for all
$q\leq p$
such that for all
![]() $m\in \omega $
, for all
$m\in \omega $
, for all
![]() $t\in \operatorname {\mathrm {split}}_m(q)$
there is
$t\in \operatorname {\mathrm {split}}_m(q)$
there is
![]() $f_t\in {^{m+1}\omega }$
such that
$f_t\in {^{m+1}\omega }$
such that
![]() $q(t)\Vdash \dot {f}\upharpoonright (m+1)=\check {f}_t$
. Define
$q(t)\Vdash \dot {f}\upharpoonright (m+1)=\check {f}_t$
. Define
![]() $g\in {{}^{\omega }\omega }$
as follows:
$g\in {{}^{\omega }\omega }$
as follows:
Then
![]() $q\Vdash \forall n (\dot {f}(n)<g(n))$
.
$q\Vdash \forall n (\dot {f}(n)<g(n))$
.
2.2 Preservation of P-points
Next, we show that Miller partition forcing preserves P-points. We will make use of the following notation: Given
![]() $\mathcal {G}\subseteq \mathcal {P}(\omega )$
, let
$\mathcal {G}\subseteq \mathcal {P}(\omega )$
, let
![]() $\langle \mathcal {G}\rangle _{{\mathrm{up}}}=\{X\in \mathcal {P}(\omega )\colon \exists G\in \mathcal {G}(G\subseteq X)\}$
and
$\langle \mathcal {G}\rangle _{{\mathrm{up}}}=\{X\in \mathcal {P}(\omega )\colon \exists G\in \mathcal {G}(G\subseteq X)\}$
and
![]() $\langle \mathcal {G}\rangle _{{\mathrm{dn}}}=\{X\in \mathcal {P}(\omega )\colon \exists G\in \mathcal {G}(X\subseteq G)\}$
.
$\langle \mathcal {G}\rangle _{{\mathrm{dn}}}=\{X\in \mathcal {P}(\omega )\colon \exists G\in \mathcal {G}(X\subseteq G)\}$
.
Theorem 2.10. The forcing notion
![]() $\mathbb {Q}(\mathcal {C})$
preserves P-points and Ramsey ultrafilters.
$\mathbb {Q}(\mathcal {C})$
preserves P-points and Ramsey ultrafilters.
Proof We prove just the first part. The second claim follows from the first one and the fact that the forcing notion
![]() $\mathbb {Q}(\mathcal {C})$
is
$\mathbb {Q}(\mathcal {C})$
is
![]() ${}^{\omega }\omega $
-bounding (see [Reference Halbeisen26, Lemma 21.12]). Note that a filter base
${}^{\omega }\omega $
-bounding (see [Reference Halbeisen26, Lemma 21.12]). Note that a filter base
![]() $\mathcal {G}$
generates an ultrafilter on
$\mathcal {G}$
generates an ultrafilter on
![]() $\omega $
if and only if
$\omega $
if and only if
![]() $\mathcal {P}(\omega )=\langle \mathcal {G}\rangle _{{\mathrm{up}}}\cup \langle \mathcal {G}^{\ast }\rangle _{{\mathrm{dn}}}$
.
$\mathcal {P}(\omega )=\langle \mathcal {G}\rangle _{{\mathrm{up}}}\cup \langle \mathcal {G}^{\ast }\rangle _{{\mathrm{dn}}}$
.
Let
![]() $\mathcal {U}$
be a P-point in V. We shall prove that the family
$\mathcal {U}$
be a P-point in V. We shall prove that the family
![]() $\mathcal {U}$
generates an ultrafilter in
$\mathcal {U}$
generates an ultrafilter in
![]() $V^{\mathbb {Q}(\mathcal {C})}$
, i.e.,
$V^{\mathbb {Q}(\mathcal {C})}$
, i.e.,
![]() $V^{\mathbb {Q}(\mathcal {C})}\vDash \mathcal {P}(\omega )=\langle \mathcal {U}\rangle _{{\mathrm{up}}}\cup \langle \mathcal {U}^{\ast }\rangle _{{\mathrm{dn}}}$
. Fix
$V^{\mathbb {Q}(\mathcal {C})}\vDash \mathcal {P}(\omega )=\langle \mathcal {U}\rangle _{{\mathrm{up}}}\cup \langle \mathcal {U}^{\ast }\rangle _{{\mathrm{dn}}}$
. Fix
![]() $p\in \mathbb {Q}(\mathcal {C})$
and a
$p\in \mathbb {Q}(\mathcal {C})$
and a
![]() $\mathbb {Q}(\mathcal {C})$
-name
$\mathbb {Q}(\mathcal {C})$
-name
![]() $\dot {Y}$
such that
$\dot {Y}$
such that
![]() $p\Vdash \dot {Y}\subseteq \omega $
. By Lemma 2.8 we can assume that for all
$p\Vdash \dot {Y}\subseteq \omega $
. By Lemma 2.8 we can assume that for all
![]() $m\in \omega $
, for all
$m\in \omega $
, for all
![]() $t\in \mbox {split}_m(p)$
there is
$t\in \mbox {split}_m(p)$
there is
![]() $u_t\in {^{m+1}2}$
such that
$u_t\in {^{m+1}2}$
such that
Note that the latter property remains true for any stronger condition q, since t in the m-th level of q is an extension of some s in the m-th level of p. Let
![]() $\{x_t\colon t\in p\}\subseteq [p]$
be a dense set in
$\{x_t\colon t\in p\}\subseteq [p]$
be a dense set in
![]() $[p]$
containing
$[p]$
containing
![]() $\mathcal {C}$
-different elements (enumerated such that
$\mathcal {C}$
-different elements (enumerated such that
![]() $s\subseteq x_s$
, and if
$s\subseteq x_s$
, and if
![]() $s\subseteq t\subseteq x_s$
then
$s\subseteq t\subseteq x_s$
then
![]() $x_t=x_s$
). Let
$x_t=x_s$
). Let
![]() $Y_t=\bigcup \{u_s\colon s\subseteq x_t\}$
.
$Y_t=\bigcup \{u_s\colon s\subseteq x_t\}$
.
Claim. We can assume that
![]() $\mathcal {Y}_0\kern1.2pt{=}\kern1.2pt\{Y_s\colon s\kern1.2pt{\in}\kern1.2pt p\}\kern1.5pt{\subseteq}\kern1.5pt \mathcal {U}$
or
$\mathcal {Y}_0\kern1.2pt{=}\kern1.2pt\{Y_s\colon s\kern1.2pt{\in}\kern1.2pt p\}\kern1.5pt{\subseteq}\kern1.5pt \mathcal {U}$
or
![]() $\mathcal {Y}_1=\{\omega \setminus Y_s\colon s\kern1.2pt{\in}\kern1.2pt p\}\subseteq \mathcal {U}$
.
$\mathcal {Y}_1=\{\omega \setminus Y_s\colon s\kern1.2pt{\in}\kern1.2pt p\}\subseteq \mathcal {U}$
.
Proof We set
![]() $U_0=\{s\in p\colon Y_s\in \mathcal {U}\}$
and
$U_0=\{s\in p\colon Y_s\in \mathcal {U}\}$
and
![]() $U_1=\{s\in p\colon (\omega \setminus Y_s)\in \mathcal {U}\}$
. The sets
$U_1=\{s\in p\colon (\omega \setminus Y_s)\in \mathcal {U}\}$
. The sets
![]() $U_0, U_1$
are disjoint and their union is p. We may distinguish two cases:
$U_0, U_1$
are disjoint and their union is p. We may distinguish two cases:
-
(i) There is
 $s\in p$
such that
$s\in p$
such that
 $p(s)\subseteq U_0$
. In this case, just take
$p(s)\subseteq U_0$
. In this case, just take
 $p(s)$
.
$p(s)$
. -
(ii) For each
 $s\in p$
there is
$s\in p$
there is
 $t\in p(s)$
such that
$t\in p(s)$
such that
 $t\in U_1$
. We build a fusion sequence
$t\in U_1$
. We build a fusion sequence
 $\{(p_n,X_n)\}_{n\in \omega }$
such that the fusion has the required properties. Taking
$\{(p_n,X_n)\}_{n\in \omega }$
such that the fusion has the required properties. Taking
 $s\in \operatorname {\mathrm {split}}_0(p)$
there is
$s\in \operatorname {\mathrm {split}}_0(p)$
there is
 $t\in p(s)$
such that
$t\in p(s)$
such that
 $t\in U_1$
. We set
$t\in U_1$
. We set
 $p_0=p(t)$
and
$p_0=p(t)$
and
 $X_0=\{x_t\}$
.
$X_0=\{x_t\}$
.Let
 $0\leq n<\omega $
. Suppose we have defined
$0\leq n<\omega $
. Suppose we have defined
 $p_n\in \mathbb {Q}(\mathcal {C})$
and finite
$p_n\in \mathbb {Q}(\mathcal {C})$
and finite
 $X_n\subseteq [p_n]$
. Let
$X_n\subseteq [p_n]$
. Let
 $s\in \operatorname {\mathrm {split}}_n(p_n)$
. Take node
$s\in \operatorname {\mathrm {split}}_n(p_n)$
. Take node
 $r=x_s\restriction \operatorname {\mathrm {split}}_{n+1}(p_n)$
, and number
$r=x_s\restriction \operatorname {\mathrm {split}}_{n+1}(p_n)$
, and number
 $i=x_s(|s|)$
in
$i=x_s(|s|)$
in
 $\{0,1\}$
. We set
$\{0,1\}$
. We set
 $p(s,i)=p_n(r)$
. Let
$p(s,i)=p_n(r)$
. Let
 $t\supseteq s^{\smallfrown } \langle 1-i\rangle $
be splitting such that
$t\supseteq s^{\smallfrown } \langle 1-i\rangle $
be splitting such that
 $t\in U_1$
. We set
$t\in U_1$
. We set
 $p(s,1-i)=p(t)$
.
$p(s,1-i)=p(t)$
.Finally, let
and let $$\begin{align*}p_{n+1}=\bigcup\{p(s,i)\colon s\in\operatorname{\mathrm{split}}_n(p_n), i\in\{0,1\}\}. \end{align*}$$
$$\begin{align*}p_{n+1}=\bigcup\{p(s,i)\colon s\in\operatorname{\mathrm{split}}_n(p_n), i\in\{0,1\}\}. \end{align*}$$
 $X_{n+1}$
be the set of all
$X_{n+1}$
be the set of all
 $x_t$
’s for
$x_t$
’s for
 $t\in \operatorname {\mathrm {split}}_{n+1}(p_{n+1})$
. One can verify that the sequence
$t\in \operatorname {\mathrm {split}}_{n+1}(p_{n+1})$
. One can verify that the sequence
 $\{(p_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses. Moreover the fusion q of this sequence satisfies that
$\{(p_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses. Moreover the fusion q of this sequence satisfies that
 $(\omega \backslash Y_s)\in \mathcal {U}$
for all
$(\omega \backslash Y_s)\in \mathcal {U}$
for all
 $s\in q$
.
$s\in q$
.
We assume that
![]() $\mathcal {Y}_0\subseteq \mathcal {U}$
, the other case may be handled analogously. We take a pseudointersection Z of
$\mathcal {Y}_0\subseteq \mathcal {U}$
, the other case may be handled analogously. We take a pseudointersection Z of
![]() $\mathcal {Y}_0$
in
$\mathcal {Y}_0$
in
![]() $\mathcal {U}$
, with
$\mathcal {U}$
, with
![]() $Z\subseteq Y_{\emptyset }$
. We shall simultaneously build two fusion sequences with witnesses, namely
$Z\subseteq Y_{\emptyset }$
. We shall simultaneously build two fusion sequences with witnesses, namely
![]() $\{(p^0_n,X^0_n)\}_{n\in \omega }$
,
$\{(p^0_n,X^0_n)\}_{n\in \omega }$
,
![]() $\{(p^1_n,X^1_n)\}_{n\in \omega }$
, and a partition of Z into two sets
$\{(p^1_n,X^1_n)\}_{n\in \omega }$
, and a partition of Z into two sets
![]() $Z_0$
,
$Z_0$
,
![]() $Z_1$
such that for their respective fusions
$Z_1$
such that for their respective fusions
![]() $q_0,q_1\leq p$
we obtain
$q_0,q_1\leq p$
we obtain
![]() $q_0\Vdash \check {Z}_0\subseteq \dot {Y}$
and
$q_0\Vdash \check {Z}_0\subseteq \dot {Y}$
and
![]() $q_1\Vdash \check {Z}_1\subseteq \dot {Y}$
.
$q_1\Vdash \check {Z}_1\subseteq \dot {Y}$
.
Let
![]() $p^0_0=p^1_0=p$
,
$p^0_0=p^1_0=p$
,
![]() $X^0_0=X^1_0=\{Y_{\emptyset }\}$
, and
$X^0_0=X^1_0=\{Y_{\emptyset }\}$
, and
![]() $k_0=0$
,
$k_0=0$
,
![]() $k_1=2$
. We assume that
$k_1=2$
. We assume that
![]() $p^0_n$
,
$p^0_n$
,
![]() $p^1_n$
,
$p^1_n$
,
![]() $k_{2n}$
, and
$k_{2n}$
, and
![]() $k_{2n+1}$
are constructed. Let
$k_{2n+1}$
are constructed. Let
![]() $t\in \operatorname {\mathrm {split}}_{k_{2n}}(p)\cap \operatorname {\mathrm {split}}(p^0_n)$
, and set
$t\in \operatorname {\mathrm {split}}_{k_{2n}}(p)\cap \operatorname {\mathrm {split}}(p^0_n)$
, and set
![]() $w^{\ast }(t)=x_t\restriction \operatorname {\mathrm {split}}_{k_{2n+1}}(p)$
. For each
$w^{\ast }(t)=x_t\restriction \operatorname {\mathrm {split}}_{k_{2n+1}}(p)$
. For each
![]() $i\in \{0,1\}$
, we take
$i\in \{0,1\}$
, we take
![]() $w^{\ast }(t,i)\in \operatorname {\mathrm {split}}_{k_{2n+1}+1}(p)$
extending
$w^{\ast }(t,i)\in \operatorname {\mathrm {split}}_{k_{2n+1}+1}(p)$
extending
![]() $w^{\ast }(t)^{\smallfrown } i$
. There is
$w^{\ast }(t)^{\smallfrown } i$
. There is
![]() $k_{2n+2}>k_{2n+1}+1$
such that
$k_{2n+2}>k_{2n+1}+1$
such that
We set
![]() $w(t,i)=x_{w^{\ast }(t,i)}\restriction \operatorname {\mathrm {split}}_{k_{2n+2}}(p)$
. Take
$w(t,i)=x_{w^{\ast }(t,i)}\restriction \operatorname {\mathrm {split}}_{k_{2n+2}}(p)$
. Take
![]() $p_{n+1}^0=\bigcup \{p(w(t,i))\colon t\in \operatorname {\mathrm {split}}_{k_{2n}}(p)\cap \operatorname {\mathrm {split}}(p^0_n), i\in \{0,1\}\}$
and
$p_{n+1}^0=\bigcup \{p(w(t,i))\colon t\in \operatorname {\mathrm {split}}_{k_{2n}}(p)\cap \operatorname {\mathrm {split}}(p^0_n), i\in \{0,1\}\}$
and
![]() $X_{n+1}^0=\{x_{w(t,i)}\colon t\in \operatorname {\mathrm {split}}_{k_{2n}}(p)\cap \operatorname {\mathrm {split}}(p^0_n), i\in \{0,1\}\}$
. One can see that
$X_{n+1}^0=\{x_{w(t,i)}\colon t\in \operatorname {\mathrm {split}}_{k_{2n}}(p)\cap \operatorname {\mathrm {split}}(p^0_n), i\in \{0,1\}\}$
. One can see that
![]() $p^0_n\Vdash \check {Z}\cap [k_{2n},k_{2n+1})\subseteq \dot {Y}$
. The construction of condition
$p^0_n\Vdash \check {Z}\cap [k_{2n},k_{2n+1})\subseteq \dot {Y}$
. The construction of condition
![]() $p^1_n$
and the choice of number
$p^1_n$
and the choice of number
![]() $k_{2n+3}$
are done similarly, and leads to
$k_{2n+3}$
are done similarly, and leads to
![]() $p^1_n\Vdash \check {Z}\cap [k_{2n+1},k_{2n+2})\subseteq \dot {Y}$
. Finally, we define
$p^1_n\Vdash \check {Z}\cap [k_{2n+1},k_{2n+2})\subseteq \dot {Y}$
. Finally, we define
Since
![]() $Z\in \mathcal {U}$
,
$Z\in \mathcal {U}$
,
![]() $Z_0$
or
$Z_0$
or
![]() $Z_1$
is in
$Z_1$
is in
![]() $\mathcal {U}$
, and so
$\mathcal {U}$
, and so
![]() $q_0\Vdash \dot {Y}\in \langle \mathcal {U}\rangle _{{\mathrm{up}}}$
or
$q_0\Vdash \dot {Y}\in \langle \mathcal {U}\rangle _{{\mathrm{up}}}$
or
![]() $q_1\Vdash \dot {Y}\in \langle \mathcal {U}\rangle _{{\mathrm{up}}}$
.
$q_1\Vdash \dot {Y}\in \langle \mathcal {U}\rangle _{{\mathrm{up}}}$
.
3 Selective independence
3.1 Dense maximality
Recall the definition:
Definition 3.1. A family
![]() $\mathcal {A}\subseteq \mathcal {P}(\omega )$
is an independent family if for every distinct
$\mathcal {A}\subseteq \mathcal {P}(\omega )$
is an independent family if for every distinct
![]() $A_0,\dots ,A_n\in \mathcal {A}$
and
$A_0,\dots ,A_n\in \mathcal {A}$
and
![]() $h:\{A_0,\dots ,A_n\}\longrightarrow 2$
, the set
$h:\{A_0,\dots ,A_n\}\longrightarrow 2$
, the set
![]() $\bigcap \limits _{i\leq n}A_i^{h(A_i)}$
is infinite where
$\bigcap \limits _{i\leq n}A_i^{h(A_i)}$
is infinite where
![]() $A_i^0=\omega \backslash A_i$
and
$A_i^0=\omega \backslash A_i$
and
![]() $A_i^1=A_i$
. It is maximal independent, if it is independent and maximal under inclusion.
$A_i^1=A_i$
. It is maximal independent, if it is independent and maximal under inclusion.
We will be exclusively interested in infinite independent families. For an independent family
![]() $\mathcal {A}$
let
$\mathcal {A}$
let
![]() $\operatorname {\mathrm {FF}}(\mathcal {A})$
be the set of all finite partial functions from
$\operatorname {\mathrm {FF}}(\mathcal {A})$
be the set of all finite partial functions from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $2$
and order it by inclusion. For
$2$
and order it by inclusion. For
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
, we let
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
, we let
![]() $\mathcal {A}^h=\bigcap \{A^{h(A)}\;|\; A\in dom(h)\}$
where
$\mathcal {A}^h=\bigcap \{A^{h(A)}\;|\; A\in dom(h)\}$
where
![]() $A^0=\omega \backslash A$
and
$A^0=\omega \backslash A$
and
![]() $A^1=A$
for
$A^1=A$
for
![]() $A\subseteq \omega $
. The density ideal of
$A\subseteq \omega $
. The density ideal of
![]() $\mathcal {A}$
, denoted
$\mathcal {A}$
, denoted
![]() ${\mathrm {id}}(\mathcal {A})$
is the set of all
${\mathrm {id}}(\mathcal {A})$
is the set of all
![]() $X\subseteq \omega $
such that for all
$X\subseteq \omega $
such that for all
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
there is
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
there is
![]() $h'\supseteq h$
in
$h'\supseteq h$
in
![]() $\operatorname {\mathrm {FF}}(\mathcal {A})$
such that
$\operatorname {\mathrm {FF}}(\mathcal {A})$
such that
![]() $\mathcal {A}^{h'}\cap X$
is finite (or equivalently empty). Dual to the density ideal of
$\mathcal {A}^{h'}\cap X$
is finite (or equivalently empty). Dual to the density ideal of
![]() $\mathcal {A}$
is the density filter of
$\mathcal {A}$
is the density filter of
![]() $\mathcal {A}$
denoted
$\mathcal {A}$
denoted
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})$
and consisting of all
$\operatorname {\mathrm {fil}}(\mathcal {A})$
and consisting of all
![]() $X\subseteq \omega $
such that for all
$X\subseteq \omega $
such that for all
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
there is
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
there is
![]() $h'\supseteq h$
in
$h'\supseteq h$
in
![]() $\operatorname {\mathrm {FF}}(\mathcal {A})$
such that
$\operatorname {\mathrm {FF}}(\mathcal {A})$
such that
![]() $\mathcal {A}^{h'}\backslash X$
is finite (or equivalently empty).Footnote
3
$\mathcal {A}^{h'}\backslash X$
is finite (or equivalently empty).Footnote
3
Lemma 3.2. Let
![]() $\mathcal {A}$
be an infinite independent family. The following are equivalent:
$\mathcal {A}$
be an infinite independent family. The following are equivalent:
-
(1) For all
 $X\in \mathcal {P}(\omega )$
and all
$X\in \mathcal {P}(\omega )$
and all
 $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
there is
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
there is
 $h'\supseteq h$
such that
$h'\supseteq h$
such that
 $\mathcal {A}^{h'}\cap X$
or
$\mathcal {A}^{h'}\cap X$
or
 $\mathcal {A}^{h'}\backslash X$
is finite.
$\mathcal {A}^{h'}\backslash X$
is finite. -
(2) For all
 $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
and all
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
and all
 $X\subseteq \mathcal {A}^h$
either
$X\subseteq \mathcal {A}^h$
either
 $\mathcal {A}^h\backslash X\in {\mathrm {id}}(\mathcal {A})$
or there is
$\mathcal {A}^h\backslash X\in {\mathrm {id}}(\mathcal {A})$
or there is
 $h'\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that
$h'\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that
 $h'\supseteq h$
and
$h'\supseteq h$
and
 $\mathcal {A}^{h'}\subseteq \mathcal {A}^h\backslash X$
.
$\mathcal {A}^{h'}\subseteq \mathcal {A}^h\backslash X$
. -
(3) For each
 $X\in \mathcal {P}(\omega )\backslash \operatorname {\mathrm {fil}}(\mathcal {A})$
there is
$X\in \mathcal {P}(\omega )\backslash \operatorname {\mathrm {fil}}(\mathcal {A})$
there is
 $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that
 $X\subseteq \omega \backslash \mathcal {A}^h$
.
$X\subseteq \omega \backslash \mathcal {A}^h$
.
Proof First we show that
![]() $(1)$
implies
$(1)$
implies
![]() $(2)$
. Let
$(2)$
. Let
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
, let
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
, let
![]() $X\subseteq \mathcal {A}^h$
, and suppose
$X\subseteq \mathcal {A}^h$
, and suppose
![]() $\mathcal {A}^h\backslash X\notin {\mathrm {id}}(\mathcal {A})$
. Thus, there is
$\mathcal {A}^h\backslash X\notin {\mathrm {id}}(\mathcal {A})$
. Thus, there is
![]() $h'\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that for all
$h'\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that for all
![]() $h"\supseteq h'$
the set
$h"\supseteq h'$
the set
![]() $\mathcal {A}^{h\prime \prime }\cap (\mathcal {A}^h\backslash X)$
is non-empty. Note that if h and
$\mathcal {A}^{h\prime \prime }\cap (\mathcal {A}^h\backslash X)$
is non-empty. Note that if h and
![]() $h'$
are incompatible, then
$h'$
are incompatible, then
![]() $\mathcal {A}^{h'}\cap (\mathcal {A}^h\backslash X)=\emptyset $
, which is a contradiction. Therefore h and
$\mathcal {A}^{h'}\cap (\mathcal {A}^h\backslash X)=\emptyset $
, which is a contradiction. Therefore h and
![]() $h'$
are compatible and without loss of generality, we can assume that
$h'$
are compatible and without loss of generality, we can assume that
![]() $h'\supseteq h$
. Thus, we have that for all
$h'\supseteq h$
. Thus, we have that for all
![]() $h"\supseteq h'$
, the set
$h"\supseteq h'$
, the set
![]() $\mathcal {A}^{h\prime \prime }\backslash X\neq \emptyset $
. Now, since
$\mathcal {A}^{h\prime \prime }\backslash X\neq \emptyset $
. Now, since
![]() $(1)$
holds, there is
$(1)$
holds, there is
![]() $h"\supseteq h'$
such that
$h"\supseteq h'$
such that
![]() $\mathcal {A}^{h\prime \prime }\cap X=\emptyset $
. That is,
$\mathcal {A}^{h\prime \prime }\cap X=\emptyset $
. That is,
![]() $\mathcal {A}^{h\prime \prime }\subseteq \mathcal {A}^{h}\backslash X$
.
$\mathcal {A}^{h\prime \prime }\subseteq \mathcal {A}^{h}\backslash X$
.
Next, we show that
![]() $(2)$
implies
$(2)$
implies
![]() $(3)$
. Thus, consider any
$(3)$
. Thus, consider any
![]() $X\in \mathcal {P}(\omega )\backslash \operatorname {\mathrm {fil}}(\mathcal {A})$
. Then, in particular
$X\in \mathcal {P}(\omega )\backslash \operatorname {\mathrm {fil}}(\mathcal {A})$
. Then, in particular
![]() $\omega \backslash X\notin {\mathrm {id}}(\mathcal {A})$
and so there is
$\omega \backslash X\notin {\mathrm {id}}(\mathcal {A})$
and so there is
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that for all
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that for all
![]() $h'\supseteq h$
,
$h'\supseteq h$
,
![]() $|\mathcal {A}^{h'}\cap (\omega \backslash X)|=|\mathcal {A}^{h'}\backslash X|=\omega $
. Let
$|\mathcal {A}^{h'}\cap (\omega \backslash X)|=|\mathcal {A}^{h'}\backslash X|=\omega $
. Let
![]() $Y=\mathcal {A}^h\backslash X$
. Thus,
$Y=\mathcal {A}^h\backslash X$
. Thus,
![]() $Y\subseteq \mathcal {A}^h$
. By part
$Y\subseteq \mathcal {A}^h$
. By part
![]() $(2)$
either
$(2)$
either
![]() $\mathcal {A}^h\backslash Y\in {\mathrm {id}}(\mathcal {A})$
or there is
$\mathcal {A}^h\backslash Y\in {\mathrm {id}}(\mathcal {A})$
or there is
![]() $h'\supseteq h$
such that
$h'\supseteq h$
such that
![]() $\mathcal {A}^{h'}\subseteq \mathcal {A}^h\backslash Y$
. Suppose
$\mathcal {A}^{h'}\subseteq \mathcal {A}^h\backslash Y$
. Suppose
![]() $\mathcal {A}^h\backslash Y\in {\mathrm {id}}(\mathcal {A})$
. Then, there is
$\mathcal {A}^h\backslash Y\in {\mathrm {id}}(\mathcal {A})$
. Then, there is
![]() $h'\supseteq h$
such that
$h'\supseteq h$
such that
![]() $\mathcal {A}^{h'}\cap (\mathcal {A}^h\backslash Y)=\mathcal {A}^{h'}\backslash Y=\emptyset $
. However
$\mathcal {A}^{h'}\cap (\mathcal {A}^h\backslash Y)=\mathcal {A}^{h'}\backslash Y=\emptyset $
. However
![]() $\mathcal {A}^{h'}\backslash Y=\mathcal {A}^{h'}\cap X=\emptyset $
and so
$\mathcal {A}^{h'}\backslash Y=\mathcal {A}^{h'}\cap X=\emptyset $
and so
![]() $X\subseteq \omega \backslash \mathcal {A}^{h'}$
and we are done. If there is
$X\subseteq \omega \backslash \mathcal {A}^{h'}$
and we are done. If there is
![]() $h'\supseteq h$
such that
$h'\supseteq h$
such that
![]() $\mathcal {A}^{h'}\subseteq \mathcal {A}^h\backslash Y=\mathcal {A}^h\cap X$
, then
$\mathcal {A}^{h'}\subseteq \mathcal {A}^h\backslash Y=\mathcal {A}^h\cap X$
, then
![]() $\mathcal {A}^{h'}\cap (\omega \backslash X)=\mathcal {A}^{h'}\backslash X=\emptyset $
, contradicting the choice of h.
$\mathcal {A}^{h'}\cap (\omega \backslash X)=\mathcal {A}^{h'}\backslash X=\emptyset $
, contradicting the choice of h.
To see that
![]() $(3)$
implies
$(3)$
implies
![]() $(2)$
, consider any
$(2)$
, consider any
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
and
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
and
![]() $X\subseteq \mathcal {A}^h$
. Let
$X\subseteq \mathcal {A}^h$
. Let
![]() $Y=\mathcal {A}^h\backslash X$
. If
$Y=\mathcal {A}^h\backslash X$
. If
![]() $\omega \backslash Y\in \operatorname {\mathrm {fil}}(\mathcal {A})$
, then
$\omega \backslash Y\in \operatorname {\mathrm {fil}}(\mathcal {A})$
, then
![]() $Y=\mathcal {A}^h\backslash X\in {\mathrm {id}}(\mathcal {A})$
. Otherwise, there is
$Y=\mathcal {A}^h\backslash X\in {\mathrm {id}}(\mathcal {A})$
. Otherwise, there is
![]() $h^*$
such that
$h^*$
such that
![]() $\omega \backslash Y\subseteq \omega \backslash \mathcal {A}^{h^*}$
, which implies that
$\omega \backslash Y\subseteq \omega \backslash \mathcal {A}^{h^*}$
, which implies that
![]() $\mathcal {A}^{h^*}\subseteq Y=\mathcal {A}^h\backslash X$
and so
$\mathcal {A}^{h^*}\subseteq Y=\mathcal {A}^h\backslash X$
and so
![]() $\mathcal {A}^{h^*\cup h}\subseteq \mathcal {A}^{h^*}\subseteq \mathcal {A}^h\backslash X$
.
$\mathcal {A}^{h^*\cup h}\subseteq \mathcal {A}^{h^*}\subseteq \mathcal {A}^h\backslash X$
.
To see that
![]() $(2)$
implies
$(2)$
implies
![]() $(1)$
consider any
$(1)$
consider any
![]() $X\in [\omega ]^{\omega }$
and let
$X\in [\omega ]^{\omega }$
and let
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
. We want to show that there is
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
. We want to show that there is
![]() $h'\supseteq h$
such that either
$h'\supseteq h$
such that either
![]() $\mathcal {A}^{h'}\cap X=\emptyset $
, or
$\mathcal {A}^{h'}\cap X=\emptyset $
, or
![]() $\mathcal {A}^{h'}\backslash X=\emptyset $
. Let
$\mathcal {A}^{h'}\backslash X=\emptyset $
. Let
![]() $Y=X\cap \mathcal {A}^h$
. Thus,
$Y=X\cap \mathcal {A}^h$
. Thus,
![]() $Y\subseteq \mathcal {A}^h$
. If
$Y\subseteq \mathcal {A}^h$
. If
![]() $\mathcal {A}^h\backslash Y\in {\mathrm {id}}(\mathcal {A})$
, then
$\mathcal {A}^h\backslash Y\in {\mathrm {id}}(\mathcal {A})$
, then
![]() $\mathcal {A}^h\backslash X\in {\mathrm {id}}(\mathcal {A})$
and so there is
$\mathcal {A}^h\backslash X\in {\mathrm {id}}(\mathcal {A})$
and so there is
![]() $h'\supseteq h$
such that
$h'\supseteq h$
such that
![]() $\mathcal {A}^{h'}\cap (\mathcal {A}^h\backslash X)=\mathcal {A}^{h'}\backslash X=\emptyset $
. Otherwise, there is
$\mathcal {A}^{h'}\cap (\mathcal {A}^h\backslash X)=\mathcal {A}^{h'}\backslash X=\emptyset $
. Otherwise, there is
![]() $h'\supseteq h$
such that
$h'\supseteq h$
such that
![]() $\mathcal {A}^{h'}\subseteq \mathcal {A}^h\backslash Y$
and so
$\mathcal {A}^{h'}\subseteq \mathcal {A}^h\backslash Y$
and so
![]() $\mathcal {A}^{h'}\cap Y=\emptyset $
. However,
$\mathcal {A}^{h'}\cap Y=\emptyset $
. However,
![]() $\mathcal {A}^{h'}\cap Y=\mathcal {A}^{h'}\cap (X\cap \mathcal {A}^h)=\mathcal {A}^{h'}\cap X=\emptyset $
.
$\mathcal {A}^{h'}\cap Y=\mathcal {A}^{h'}\cap (X\cap \mathcal {A}^h)=\mathcal {A}^{h'}\cap X=\emptyset $
.
An independent family
![]() $\mathcal {A}$
is said to be densely maximal if any one of the above three properties holds. Note that if an independent family is densely maximal, then it is also maximal. The notion of dense maximality of independent families appears (to the best knowledge of the authors) for the first time in [Reference Goldstern and Shelah24]. In particular, we obtain:
$\mathcal {A}$
is said to be densely maximal if any one of the above three properties holds. Note that if an independent family is densely maximal, then it is also maximal. The notion of dense maximality of independent families appears (to the best knowledge of the authors) for the first time in [Reference Goldstern and Shelah24]. In particular, we obtain:
Corollary 3.3. Let
![]() $\mathcal {A}$
be an infinite independent family. Then,
$\mathcal {A}$
be an infinite independent family. Then,
![]() $\mathcal {A}$
is densely maximal iff
$\mathcal {A}$
is densely maximal iff
The fact that partial orders has the Sacks property implies in particular:
Lemma 3.4 [Reference Chodounský, Fischer and Grebík14].
Let W be a
![]() $\mathbb {P}$
-generic extension of V, where
$\mathbb {P}$
-generic extension of V, where
![]() $\mathbb {P}$
has the Sacks property. If
$\mathbb {P}$
has the Sacks property. If
![]() $\mathcal {A}\in V$
is an independent family, then in W,
$\mathcal {A}\in V$
is an independent family, then in W,
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})$
is generated by
$\operatorname {\mathrm {fil}}(\mathcal {A})$
is generated by
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})^V$
.
$\operatorname {\mathrm {fil}}(\mathcal {A})^V$
.
3.2 Selectivity
Recall the following definitions. Let
![]() $\mathcal {F}\subseteq \mathcal {P}(\omega )$
. Then
$\mathcal {F}\subseteq \mathcal {P}(\omega )$
. Then
![]() $\mathcal {F}$
is centered if for every finite subfamily
$\mathcal {F}$
is centered if for every finite subfamily
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
![]() $\bigcap \mathcal {H}\in \mathcal {F}$
;
$\bigcap \mathcal {H}\in \mathcal {F}$
;
![]() $\mathcal {F}$
is a P-set, if every countable subfamily has a pseudo-intersection in
$\mathcal {F}$
is a P-set, if every countable subfamily has a pseudo-intersection in
![]() $\mathcal {F}$
;
$\mathcal {F}$
;
![]() $\mathcal {F}$
is a Q-set, if for every partition
$\mathcal {F}$
is a Q-set, if for every partition
![]() $\mathcal {E}$
of
$\mathcal {E}$
of
![]() $\omega $
into finite sets, there is an
$\omega $
into finite sets, there is an
![]() $X\in \mathcal {F}$
meeting each element of the partition in at most one point, i.e.,
$X\in \mathcal {F}$
meeting each element of the partition in at most one point, i.e.,
![]() $|X\cap E|\leq 1$
for each
$|X\cap E|\leq 1$
for each
![]() $E\in \mathcal {E}$
.
$E\in \mathcal {E}$
.
Definition 3.5. Let
![]() $\mathcal {F}$
be a filter over
$\mathcal {F}$
be a filter over
![]() $\omega $
containing the Fréchet filter. We say that
$\omega $
containing the Fréchet filter. We say that
![]() $\mathcal {F}$
is a selective filter if and only if for every partition
$\mathcal {F}$
is a selective filter if and only if for every partition
![]() $\{X_i\}_{i\in \omega }$
of
$\{X_i\}_{i\in \omega }$
of
![]() $\omega $
into elements of
$\omega $
into elements of
![]() $\mathcal {F}^*$
, where
$\mathcal {F}^*$
, where
![]() $\mathcal {F}^*$
is the dual ideal of
$\mathcal {F}^*$
is the dual ideal of
![]() $\mathcal {F}$
, there exists
$\mathcal {F}$
, there exists
![]() $Y\in \mathcal {F}$
such that
$Y\in \mathcal {F}$
such that
![]() $|Y\cap X_i|\leq 1$
for each
$|Y\cap X_i|\leq 1$
for each
![]() $i\in \omega $
.
$i\in \omega $
.
Note that a filter
![]() $\mathcal {F}\subseteq \mathcal {P}(\omega )$
is selective (also called Ramsey) if and only if
$\mathcal {F}\subseteq \mathcal {P}(\omega )$
is selective (also called Ramsey) if and only if
![]() $\mathcal {F}$
extends the Fréchet filter and is both a P-set and a Q-set.
$\mathcal {F}$
extends the Fréchet filter and is both a P-set and a Q-set.
Definition 3.6. An independent family is said to be selective if it is densely maximal and
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})$
is a selective filter.
$\operatorname {\mathrm {fil}}(\mathcal {A})$
is a selective filter.
Selective independent families exist under
![]() $\textsf {CH}$
, a result which is due to Shelah (see [Reference Shelah46]). Further studies of selective independent families can be found in [Reference Chodounský, Fischer and Grebík14, Reference Fischer and Montoya17].
$\textsf {CH}$
, a result which is due to Shelah (see [Reference Shelah46]). Further studies of selective independent families can be found in [Reference Chodounský, Fischer and Grebík14, Reference Fischer and Montoya17].
Of particular interest for us will be the following combinatorial characterization of Q-filters which is similar to a characterization of happy families (see Proposition 0.7 in the work of Mathias [Reference Mathias37] or Proposition 11.6 in [Reference Halbeisen26]), as well as the fact that Q-filters are preserved by
![]() $^{\omega }\omega $
-bounding forcing notions (see Lemma 3.8).
$^{\omega }\omega $
-bounding forcing notions (see Lemma 3.8).
Lemma 3.7. Let
![]() $\mathcal {F}$
be a filter. The following are equivalent:
$\mathcal {F}$
be a filter. The following are equivalent:
-
(a)
 $\mathcal {F}$
is a Q-filter.
$\mathcal {F}$
is a Q-filter. -
(b) For any increasing function
 $f\in {{}^{\omega }\omega }$
there is
$f\in {{}^{\omega }\omega }$
there is
 $\{k(n)\colon n\in \omega \}\in \mathcal {F}$
such that
$\{k(n)\colon n\in \omega \}\in \mathcal {F}$
such that
 $f(k(n))<k(n+1)$
.
$f(k(n))<k(n+1)$
.
Proof
![]() $(\mathrm {(a)}\Rightarrow \mathrm {(b)})$
Note that the partition relations occurring in this proof, and so implicitly the proof itself, can be found in [Reference Shelah46]. Inductively, choose a sequence
$(\mathrm {(a)}\Rightarrow \mathrm {(b)})$
Note that the partition relations occurring in this proof, and so implicitly the proof itself, can be found in [Reference Shelah46]. Inductively, choose a sequence
![]() $\{n(l)\}_{l\in \omega }$
such that
$\{n(l)\}_{l\in \omega }$
such that
![]() $n(0)=0$
and
$n(0)=0$
and
We consider the partition
![]() $\mathcal {E}_0=\{[n(3l), n(3l+3))\}_{l\in \omega }$
. There is
$\mathcal {E}_0=\{[n(3l), n(3l+3))\}_{l\in \omega }$
. There is
![]() $C_1\in \mathcal {F}$
such that
$C_1\in \mathcal {F}$
such that
![]() $C_1$
is a selector for
$C_1$
is a selector for
![]() $\mathcal {E}_0$
. Now, consider the relation
$\mathcal {E}_0$
. Now, consider the relation
![]() $\mathcal {E}_1$
on
$\mathcal {E}_1$
on
![]() $C_1$
defined as follows:
$C_1$
defined as follows:
Note that
![]() $\mathcal {E}_1$
is clearly reflexive and symmetric. Transitivity holds, since no three pairwise distinct elements of
$\mathcal {E}_1$
is clearly reflexive and symmetric. Transitivity holds, since no three pairwise distinct elements of
![]() $C_1$
are
$C_1$
are
![]() $\mathcal {E}_1$
-equivalent: Indeed, suppose
$\mathcal {E}_1$
-equivalent: Indeed, suppose
![]() $m_1<m_2<m_3$
are such that
$m_1<m_2<m_3$
are such that
![]() $m_1\mathcal {E}_1 m_2$
and
$m_1\mathcal {E}_1 m_2$
and
![]() $m_2\mathcal {E}_1 m_3$
. Then
$m_2\mathcal {E}_1 m_3$
. Then
![]() $m_1<m_2<m_3\leq f(m_1)$
. There are
$m_1<m_2<m_3\leq f(m_1)$
. There are
![]() $l_1<l_2<l_3$
such that
$l_1<l_2<l_3$
such that
![]() $m_i\in [n(3l_i), n(3l_i+3))$
. Then
$m_i\in [n(3l_i), n(3l_i+3))$
. Then
![]() $m_1<n(3l_2)\leq m_2<n(3l_3)\leq m_3\leq f(m_1)$
. However, on the other hand by the definition of sequence
$m_1<n(3l_2)\leq m_2<n(3l_3)\leq m_3\leq f(m_1)$
. However, on the other hand by the definition of sequence
![]() $\{n(l)\}_{l\in \omega }$
we have
$\{n(l)\}_{l\in \omega }$
we have
![]() $f(m_1)\leq n(3l_2+1)<n(3l_3)$
, a contradiction. Thus,
$f(m_1)\leq n(3l_2+1)<n(3l_3)$
, a contradiction. Thus,
![]() $\mathcal {E}_1$
is an equivalence relation on
$\mathcal {E}_1$
is an equivalence relation on
![]() $C_1$
and each
$C_1$
and each
![]() $\mathcal {E}_1$
-equivalence class has at most two elements.
$\mathcal {E}_1$
-equivalence class has at most two elements.
Extend
![]() $\mathcal {E}_1$
to an equivalence relation
$\mathcal {E}_1$
to an equivalence relation
![]() $\mathcal {E}_2$
on
$\mathcal {E}_2$
on
![]() $\omega $
by defining
$\omega $
by defining
There is
![]() $C_2$
in
$C_2$
in
![]() $\mathcal {F}$
such that
$\mathcal {F}$
such that
![]() $C_2$
is a selector for
$C_2$
is a selector for
![]() $\mathcal {E}_2$
. Without loss of generality
$\mathcal {E}_2$
. Without loss of generality
![]() $C_2\subseteq C_1$
and
$C_2\subseteq C_1$
and
![]() $0\in C_2$
. Let
$0\in C_2$
. Let
![]() $\{k(n)\}_{n\in \omega }$
enumerate in increasing order
$\{k(n)\}_{n\in \omega }$
enumerate in increasing order
![]() $C_2$
. Thus for all
$C_2$
. Thus for all
![]() $n,n'$
we have that
$n,n'$
we have that
![]() $k(n)\not \sim _{\mathcal {E}_2} k(n')$
. Thus, if
$k(n)\not \sim _{\mathcal {E}_2} k(n')$
. Thus, if
![]() $n<n'$
then
$n<n'$
then
![]() $k(n')\not \leq f(k(n))$
and so for all
$k(n')\not \leq f(k(n))$
and so for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $f(k(n))<k(n+1)$
.
$f(k(n))<k(n+1)$
.
![]() $(\mathrm {(b)}\Rightarrow \mathrm {(a)})$
Let
$(\mathrm {(b)}\Rightarrow \mathrm {(a)})$
Let
![]() $\mathcal {E}$
be a partition of
$\mathcal {E}$
be a partition of
![]() $\omega $
into finite sets. We set
$\omega $
into finite sets. We set
There is
![]() $\{k(n)\colon n\in \omega \}\in \mathcal {F}$
such that
$\{k(n)\colon n\in \omega \}\in \mathcal {F}$
such that
![]() $f(k(n))<k(n+1)$
for each
$f(k(n))<k(n+1)$
for each
![]() $n\in \omega $
. The set
$n\in \omega $
. The set
![]() $\{k(n)\colon n\in \omega \}$
is a selector for
$\{k(n)\colon n\in \omega \}$
is a selector for
![]() $\mathcal {E}$
. Indeed,
$\mathcal {E}$
. Indeed,
![]() $k(n)\leq f(k(n))<k(n+1)$
and therefore
$k(n)\leq f(k(n))<k(n+1)$
and therefore
![]() $k(n+1)$
is from a different set of partition
$k(n+1)$
is from a different set of partition
![]() $\mathcal {E}$
than all
$\mathcal {E}$
than all
![]() $k(i)$
for
$k(i)$
for
![]() $i\leq n$
.
$i\leq n$
.
In particular, we get the following, which we state for completeness.
Lemma 3.8. An
![]() ${}^{\omega }\omega $
-bounding forcing notion preserves Q-filters.
${}^{\omega }\omega $
-bounding forcing notion preserves Q-filters.
Proof If
![]() $\mathbb {P}$
is an
$\mathbb {P}$
is an
![]() ${}^{\omega }\omega $
-bounding forcing notion,
${}^{\omega }\omega $
-bounding forcing notion,
![]() $\mathcal {F}$
a Q-filter in V, then we use part (2) of Lemma 3.7 for
$\mathcal {F}$
a Q-filter in V, then we use part (2) of Lemma 3.7 for
![]() $f\in V\cap {{}^{\omega }\omega }$
dominating function
$f\in V\cap {{}^{\omega }\omega }$
dominating function
![]() $g\in V^{\mathbb {P}}\cap {{}^{\omega }\omega }$
.
$g\in V^{\mathbb {P}}\cap {{}^{\omega }\omega }$
.
Selective filter has a property similar to Mathias’ notion of a happy family [Reference Mathias37] (see [Reference Halbeisen26] as well). Note that Mathias [Reference Mathias37, Proposition 0.10] has shown that an ultrafilter
![]() $\mathcal {G}$
is Ramsey if and only if
$\mathcal {G}$
is Ramsey if and only if
![]() $\mathcal {G}$
is happy (see Proposition 11.7 in [Reference Halbeisen26] as well).
$\mathcal {G}$
is happy (see Proposition 11.7 in [Reference Halbeisen26] as well).
Lemma 3.9. Let
![]() $\mathcal {F}$
be a filter over
$\mathcal {F}$
be a filter over
![]() $\omega $
containing the Fréchet filter. The following are equivalent:
$\omega $
containing the Fréchet filter. The following are equivalent:
-
(a)
 $\mathcal {F}$
is selective.
$\mathcal {F}$
is selective. -
(b) For any sequence
 $\{\mathcal {G}_n\}_{n\in \omega }$
of finite subsets of
$\{\mathcal {G}_n\}_{n\in \omega }$
of finite subsets of
 $\mathcal {F}$
there is
$\mathcal {F}$
there is
 $a\in \mathcal {F}$
such that
$a\in \mathcal {F}$
such that  $$ \begin{align*} a(n+1)\in\bigcap\mathcal{G}_{a(n)}. \end{align*} $$
$$ \begin{align*} a(n+1)\in\bigcap\mathcal{G}_{a(n)}. \end{align*} $$
Proof
![]() $(\mathrm {(a)}\Rightarrow \mathrm {(b)}) \mathcal {F}$
is a P-set and therefore there is
$(\mathrm {(a)}\Rightarrow \mathrm {(b)}) \mathcal {F}$
is a P-set and therefore there is
![]() $C_0\in \mathcal {F}$
such that
$C_0\in \mathcal {F}$
such that
![]() $C_0\subseteq ^* G$
for each
$C_0\subseteq ^* G$
for each
![]() $G\in \bigcup \{\mathcal {G}_n\colon n\in \omega \}$
. Thus, for some function
$G\in \bigcup \{\mathcal {G}_n\colon n\in \omega \}$
. Thus, for some function
![]() $f\in {{}^{\omega }\omega }$
$f\in {{}^{\omega }\omega }$
Let us take
![]() $\{k(n)\colon n\in \omega \}\in \mathcal {F}$
from Lemma 3.7 such that
$\{k(n)\colon n\in \omega \}\in \mathcal {F}$
from Lemma 3.7 such that
![]() $C=\{k(n+1)\colon n\in \omega \}\subseteq C_0$
. Hence, we have
$C=\{k(n+1)\colon n\in \omega \}\subseteq C_0$
. Hence, we have
![]() $k(n+1)\in C_0\setminus f(k(n))$
, and so
$k(n+1)\in C_0\setminus f(k(n))$
, and so
![]() $k(n+1)\in \bigcap \mathcal {G}_{k(n)}$
.
$k(n+1)\in \bigcap \mathcal {G}_{k(n)}$
.
![]() $(\mathrm {(b)}\Rightarrow \mathrm {(a)})$
First we shall show that
$(\mathrm {(b)}\Rightarrow \mathrm {(a)})$
First we shall show that
![]() $\mathcal {F}$
is a P-set. Let
$\mathcal {F}$
is a P-set. Let
![]() $\{G_i\}_{i\in \omega }$
be a sequence in
$\{G_i\}_{i\in \omega }$
be a sequence in
![]() $\mathcal {F}$
. We set
$\mathcal {F}$
. We set
![]() $\mathcal {G}_i=\{G_0\cap G_1\cap \dots \cap G_i\}$
, and we take
$\mathcal {G}_i=\{G_0\cap G_1\cap \dots \cap G_i\}$
, and we take
![]() $a\in \mathcal {F}$
such that
$a\in \mathcal {F}$
such that
![]() $a(n+1)\in \bigcap \mathcal {G}_{a(n)}$
. The set a is a pseudointersection of
$a(n+1)\in \bigcap \mathcal {G}_{a(n)}$
. The set a is a pseudointersection of
![]() $\{G_i\}_{i\in \omega }$
. Indeed, if
$\{G_i\}_{i\in \omega }$
. Indeed, if
![]() $G_j$
is such that
$G_j$
is such that
![]() $j\leq a(n)$
then
$j\leq a(n)$
then
![]() $\{a(k)\colon k\geq n+1\}\subseteq G_j$
.
$\{a(k)\colon k\geq n+1\}\subseteq G_j$
.
We shall show that
![]() $\mathcal {F}$
is a Q-set using Lemma 3.7. Indeed, let the function
$\mathcal {F}$
is a Q-set using Lemma 3.7. Indeed, let the function
![]() $f\in {{}^{\omega }\omega }$
be increasing. We consider sets
$f\in {{}^{\omega }\omega }$
be increasing. We consider sets
![]() $\mathcal {G}_i=\{(f(i),+\infty )\}$
, and we take
$\mathcal {G}_i=\{(f(i),+\infty )\}$
, and we take
![]() $a\in \mathcal {F}$
such that
$a\in \mathcal {F}$
such that
![]() $a(n+1)\in \bigcap \mathcal {G}_{a(n)}$
. Hence,
$a(n+1)\in \bigcap \mathcal {G}_{a(n)}$
. Hence,
![]() $a(n+1)>f(a(n))$
.
$a(n+1)>f(a(n))$
.
The following preservation theorem will be central to the proof that iterations of Miller partition forcing, as well as other partial orders which are of interest for this article, preserve selective independent families.
Lemma 3.10 [Reference Shelah46, Lemma 3.2].
Let
![]() $\mathcal {F}$
be a selective filter and let
$\mathcal {F}$
be a selective filter and let
![]() $\mathcal {H}\subseteq P(\omega )\backslash \mathcal {F}$
be cofinal in
$\mathcal {H}\subseteq P(\omega )\backslash \mathcal {F}$
be cofinal in
![]() $P(\omega )\backslash \mathcal {F}$
with respect to
$P(\omega )\backslash \mathcal {F}$
with respect to
![]() $\subseteq ^*$
. If
$\subseteq ^*$
. If
![]() $\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\alpha }\; |\; \alpha <\delta \rangle $
is a countable support iteration of
$\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\alpha }\; |\; \alpha <\delta \rangle $
is a countable support iteration of
![]() $\omega ^{\omega }$
-bounding proper forcing notions such that for all
$\omega ^{\omega }$
-bounding proper forcing notions such that for all
![]() $\alpha <\delta $
, we have
$\alpha <\delta $
, we have
![]() then the same holds for
then the same holds for
![]() $\delta $
.
$\delta $
.
The forcing iterations, that we will be interested in, all have the Sacks property. Thus, in the corresponding generic extensions
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})$
is generated by
$\operatorname {\mathrm {fil}}(\mathcal {A})$
is generated by
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
, where V denotes the ground model (see Lemma 3.4). Thus, if
$\operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
, where V denotes the ground model (see Lemma 3.4). Thus, if
![]() $\operatorname {\mathrm {fil}}(A)$
is selective in the ground model, then it will remain selective in the desired generic extensions. Thus, the above preservation theorem implies that in order to guarantee that a given selective independent family remains selective (in our desired generic extensions), it is sufficient to guarantee that each iterand preserves the dense maximality of the family. Note that the fact that the density filter is selective will play a crucial role in this preservation arguments. That is, our techniques do not imply that densely maximal independent families are preserved, but only selective ones. Before giving detailed proofs of these crucial preservation properties of Miller partition forcing (see Theorem 4.1 and Corollary 4.10) which are also the most technical arguments in the paper, we state our main result:
$\operatorname {\mathrm {fil}}(A)$
is selective in the ground model, then it will remain selective in the desired generic extensions. Thus, the above preservation theorem implies that in order to guarantee that a given selective independent family remains selective (in our desired generic extensions), it is sufficient to guarantee that each iterand preserves the dense maximality of the family. Note that the fact that the density filter is selective will play a crucial role in this preservation arguments. That is, our techniques do not imply that densely maximal independent families are preserved, but only selective ones. Before giving detailed proofs of these crucial preservation properties of Miller partition forcing (see Theorem 4.1 and Corollary 4.10) which are also the most technical arguments in the paper, we state our main result:
Theorem 3.11. Assume CH. There is a cardinals preserving generic extension in which
Proof Let V denote the ground model. We assume that
![]() $\mathcal {A}$
is a selective independent family in V,
$\mathcal {A}$
is a selective independent family in V,
![]() $\mathcal {U}$
is a P-point in V, and
$\mathcal {U}$
is a P-point in V, and
![]() $\mathcal {E}$
is a tight MAD family in V (according to [Reference Guzmán, Hrušák and Téllez25]). Using an appropriate bookkeeping device define a countable support iteration
$\mathcal {E}$
is a tight MAD family in V (according to [Reference Guzmán, Hrušák and Téllez25]). Using an appropriate bookkeeping device define a countable support iteration
![]() $\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta }\colon \alpha \leq \omega _2,\beta <\omega _2\rangle $
of posets such that for each
$\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta }\colon \alpha \leq \omega _2,\beta <\omega _2\rangle $
of posets such that for each
![]() $\alpha $
,
$\alpha $
,
![]() $\mathbb {P}_{\alpha }$
forces that
$\mathbb {P}_{\alpha }$
forces that
![]() $\mathbb {Q}_{\alpha }=\mathbb {Q}(\mathcal {C})$
for some uncountable partition
$\mathbb {Q}_{\alpha }=\mathbb {Q}(\mathcal {C})$
for some uncountable partition
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $2^{\omega }$
into compact sets and such that
$2^{\omega }$
into compact sets and such that
![]() $V^{\mathbb {P}_{\omega _2}}\vDash \mathfrak {a}_T=\omega _2$
.
$V^{\mathbb {P}_{\omega _2}}\vDash \mathfrak {a}_T=\omega _2$
.
![]() ${\mathbb {P}_{\omega _2}}$
has the Sacks property and therefore
${\mathbb {P}_{\omega _2}}$
has the Sacks property and therefore
![]() $\operatorname {\mathrm {cof}}(\mathcal {N})=\omega _1$
. By Shelah’s preservation Theorem 3.10 and Corollary 4.10, or alternatively by Theorem 4.1, the family
$\operatorname {\mathrm {cof}}(\mathcal {N})=\omega _1$
. By Shelah’s preservation Theorem 3.10 and Corollary 4.10, or alternatively by Theorem 4.1, the family
![]() $\mathcal {A}$
remains selective independent in
$\mathcal {A}$
remains selective independent in
![]() $V^{\mathbb {P}_{\omega _2}}$
and so a witness to
$V^{\mathbb {P}_{\omega _2}}$
and so a witness to
![]() $\mathfrak {i}=\omega _1$
. Similarly,
$\mathfrak {i}=\omega _1$
. Similarly,
![]() $\mathcal {U}$
generates a P-point in
$\mathcal {U}$
generates a P-point in
![]() $V^{\mathbb {P}_{\omega _2}}$
, so
$V^{\mathbb {P}_{\omega _2}}$
, so
![]() $\mathfrak {u}=\omega _1$
as well. And finally,
$\mathfrak {u}=\omega _1$
as well. And finally,
![]() $\mathfrak {a}=\omega _1$
since
$\mathfrak {a}=\omega _1$
since
![]() $\mathcal {E}$
is a tight MAD family (see [Reference Guzmán, Hrušák and Téllez25]).
$\mathcal {E}$
is a tight MAD family (see [Reference Guzmán, Hrušák and Téllez25]).
4 Miller partition forcing preserves selective independent families
We proceed with taking care of the successor stages of our forcing construction, i.e., the fact that Miller partition forcing preserves selective independent families. In Section 4.1 using the technique of fusion with witnesses, we give a proof of this fact, while in Section 4.2 we give yet one more proof using Laflamme’s filter games.
4.1 Fusion sequences and selectivity
Theorem 4.1. Let
![]() $\mathcal {A}$
be a selective independent family and let G be a
$\mathcal {A}$
be a selective independent family and let G be a
![]() $\mathbb Q(\mathcal {C})$
-generic filter. Then, in
$\mathbb Q(\mathcal {C})$
-generic filter. Then, in
![]() $V[G]$
,
$V[G]$
,
![]() $\mathcal {A}$
is still selective independent.
$\mathcal {A}$
is still selective independent.
Proof Recall that by Lemmas 3.4 and 3.8,
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})$
remains a selective filter. Thus, it is sufficient to show that
$\operatorname {\mathrm {fil}}(\mathcal {A})$
remains a selective filter. Thus, it is sufficient to show that
![]() $\mathcal {A}$
remains densely maximal in the generic extension. In
$\mathcal {A}$
remains densely maximal in the generic extension. In
![]() $V^{\mathbb {Q}(\mathcal {C})}$
, take any
$V^{\mathbb {Q}(\mathcal {C})}$
, take any
![]() $Y\in \mathcal {P}(\omega )\backslash \langle \operatorname {\mathrm {fil}}(\mathcal {A})\cap V\rangle _{{\mathrm{up}}}$
. Suppose
$Y\in \mathcal {P}(\omega )\backslash \langle \operatorname {\mathrm {fil}}(\mathcal {A})\cap V\rangle _{{\mathrm{up}}}$
. Suppose
![]() $Y\notin \langle \{\omega \backslash \mathcal {A}^h:h\in \operatorname {\mathrm {FF}}(\mathcal {A})\}\rangle _{{\mathrm{dn}}}$
. Thus, for all
$Y\notin \langle \{\omega \backslash \mathcal {A}^h:h\in \operatorname {\mathrm {FF}}(\mathcal {A})\}\rangle _{{\mathrm{dn}}}$
. Thus, for all
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
,
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
,
![]() $Y\not \subseteq \omega \backslash \mathcal {A}^h$
and so for all
$Y\not \subseteq \omega \backslash \mathcal {A}^h$
and so for all
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
,
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
,
![]() $|Y\cap \mathcal {A}^h|=\omega $
. Therefore in V we can fix
$|Y\cap \mathcal {A}^h|=\omega $
. Therefore in V we can fix
![]() $p\in \mathbb {Q}(\mathcal {C})$
and a
$p\in \mathbb {Q}(\mathcal {C})$
and a
![]() $\mathbb {Q}(\mathcal {C})$
-name
$\mathbb {Q}(\mathcal {C})$
-name
![]() $\dot {Y}$
for Y such that for all
$\dot {Y}$
for Y such that for all
![]() $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
,
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
,
![]() $p\Vdash |\dot {Y}\cap \mathcal {A}^h|=\infty $
.
$p\Vdash |\dot {Y}\cap \mathcal {A}^h|=\infty $
.
By Lemma 2.8 we can assume that for all
![]() $m\in \omega $
, for all
$m\in \omega $
, for all
![]() $t\in \mbox {split}_m(p)$
there is
$t\in \mbox {split}_m(p)$
there is
![]() $u_t\in {^{m+1}2}$
such that
$u_t\in {^{m+1}2}$
such that
![]() $p(t)\Vdash \dot {Y}\upharpoonright (m+1)=\check {u}_t$
. Now, in V for each
$p(t)\Vdash \dot {Y}\upharpoonright (m+1)=\check {u}_t$
. Now, in V for each
![]() $t\in p$
, let
$t\in p$
, let
Claim 4.2.
-
(i)
 $p(t)\Vdash \dot {Y}\subseteq \check {Y}_t$
.
$p(t)\Vdash \dot {Y}\subseteq \check {Y}_t$
. -
(ii) If
 $s\subseteq t$
then
$s\subseteq t$
then
 $Y_t\subseteq Y_s$
.
$Y_t\subseteq Y_s$
. -
(iii)
 $Y_t\in \operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
.
$Y_t\in \operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
. -
(iv) If
 $m\in Y_s$
for
$m\in Y_s$
for
 $s\in \mbox {split}_n(p)$
, and
$s\in \mbox {split}_n(p)$
, and
 $n<m$
then there is
$n<m$
then there is
 $t\in \mbox {split}_m(p)$
extending s such that
$t\in \mbox {split}_m(p)$
extending s such that
 $p(t)\Vdash \check {m}\in \dot {Y}$
.
$p(t)\Vdash \check {m}\in \dot {Y}$
.
Proof
-
(i) Let
 $m\in \dot {Y}[G]$
for a generic G containing
$m\in \dot {Y}[G]$
for a generic G containing
 $p(t)$
. If
$p(t)$
. If
 $p(t)\Vdash \check {m}\notin \dot {Y}$
then
$p(t)\Vdash \check {m}\notin \dot {Y}$
then
 $m\notin \dot {Y}[G]$
, a contradiction.
$m\notin \dot {Y}[G]$
, a contradiction. -
(ii) Since
 $p(t)\subseteq p(s)$
, from
$p(t)\subseteq p(s)$
, from
 $p(t)\not \Vdash \check {m}\notin \dot {Y}$
we obtain
$p(t)\not \Vdash \check {m}\notin \dot {Y}$
we obtain
 $p(s)\not \Vdash \check {m}\notin \dot {Y}$
.
$p(s)\not \Vdash \check {m}\notin \dot {Y}$
. -
(iii) If
 $Y_t\notin \operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
then by Lemma 3.2(3), there is
$Y_t\notin \operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
then by Lemma 3.2(3), there is
 $h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that
$h\in \operatorname {\mathrm {FF}}(\mathcal {A})$
such that
 $Y_t\subseteq \omega \backslash \mathcal {A}^h$
, i.e.,
$Y_t\subseteq \omega \backslash \mathcal {A}^h$
, i.e.,
 $Y_t\cap \mathcal {A}^h=\emptyset $
. Since
$Y_t\cap \mathcal {A}^h=\emptyset $
. Since
 $p(t)\Vdash \dot {Y}\subseteq \check {Y}_t$
,
$p(t)\Vdash \dot {Y}\subseteq \check {Y}_t$
,
 $p(t)\Vdash \mathcal {A}^h\cap \dot {Y}=\emptyset $
. However,
$p(t)\Vdash \mathcal {A}^h\cap \dot {Y}=\emptyset $
. However,
 $p(t)\Vdash |\dot {Y}\cap \mathcal {A}^h|=\infty $
, which is a contradiction.
$p(t)\Vdash |\dot {Y}\cap \mathcal {A}^h|=\infty $
, which is a contradiction. -
(iv) Since
 $p(s)\not \Vdash \check {m}\notin \dot {Y}$
there is a condition
$p(s)\not \Vdash \check {m}\notin \dot {Y}$
there is a condition
 $q\leq p(s)$
such that
$q\leq p(s)$
such that
 $q\Vdash \check {m}\in \dot {Y}$
. However, by our assumption on p due to Lemma 2.8, for any
$q\Vdash \check {m}\in \dot {Y}$
. However, by our assumption on p due to Lemma 2.8, for any
 $t\in \mbox {split}_m(p)$
we have either
$t\in \mbox {split}_m(p)$
we have either
 $p(t)\Vdash \check {m}\in \dot {Y}$
or
$p(t)\Vdash \check {m}\in \dot {Y}$
or
 $p(t)\Vdash \check {m}\notin \dot {Y}$
. Since
$p(t)\Vdash \check {m}\notin \dot {Y}$
. Since
 $\{p(t)\colon t\in \mbox {split}_m(p), t\supseteq s\}$
is pre-dense in
$\{p(t)\colon t\in \mbox {split}_m(p), t\supseteq s\}$
is pre-dense in
 $p(s)$
, there is
$p(s)$
, there is
 $t\in \mbox {split}_m(p)$
extending s such that
$t\in \mbox {split}_m(p)$
extending s such that
 $p(t)\Vdash \check {m}\in \dot {Y}$
.
$p(t)\Vdash \check {m}\in \dot {Y}$
.
Claim 4.3. We can assume that a dense set
![]() $X\subseteq [p]$
with
$X\subseteq [p]$
with
![]() $\mathcal {C}$
-different elements has the associated family
$\mathcal {C}$
-different elements has the associated family
![]() $\{y_x\colon x\in X\}$
of sets in
$\{y_x\colon x\in X\}$
of sets in
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})$
such that if
$\operatorname {\mathrm {fil}}(\mathcal {A})$
such that if
![]() $t=x\restriction \operatorname {\mathrm {split}}_{n}(p)$
then
$t=x\restriction \operatorname {\mathrm {split}}_{n}(p)$
then
![]() $p(t)\Vdash y_x(n)\in \dot {Y}$
.
$p(t)\Vdash y_x(n)\in \dot {Y}$
.
Proof By Claim 4.2(iii),
![]() $Y_t\in \operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
for each
$Y_t\in \operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
for each
![]() $t\in \operatorname {\mathrm {split}}(p)$
. By Lemma 3.9 for
$t\in \operatorname {\mathrm {split}}(p)$
. By Lemma 3.9 for
![]() $\mathcal {G}_n$
being the family of all
$\mathcal {G}_n$
being the family of all
![]() $Y_t$
’s with
$Y_t$
’s with
![]() $t\in \operatorname {\mathrm {split}}_{\leq n}(p)$
, we obtain
$t\in \operatorname {\mathrm {split}}_{\leq n}(p)$
, we obtain
![]() $\{k(n)\colon n\in \omega \}\in \operatorname {\mathrm {fil}}(\mathcal {A})$
such that
$\{k(n)\colon n\in \omega \}\in \operatorname {\mathrm {fil}}(\mathcal {A})$
such that
Moreover, by part (iv) of Claim 4.2 for any
![]() $s\in \operatorname {\mathrm {split}}_{k(n)}(p)$
there is
$s\in \operatorname {\mathrm {split}}_{k(n)}(p)$
there is
![]() $t\in \operatorname {\mathrm {split}}_{k(n+1)}(p)$
extending s such that
$t\in \operatorname {\mathrm {split}}_{k(n+1)}(p)$
extending s such that
![]() $p(t)\Vdash \check {k}(n+1)\in \dot {Y}$
. For each branch
$p(t)\Vdash \check {k}(n+1)\in \dot {Y}$
. For each branch
![]() $x\in [p]$
we consider the set
$x\in [p]$
we consider the set
We say that
![]() $x\in [p]$
is an acceptable branch if
$x\in [p]$
is an acceptable branch if
![]() $i(x)$
is cofinite. The smallest n with
$i(x)$
is cofinite. The smallest n with
![]() $i(x)\supseteq [n,\infty )$
is called the degree of acceptability of x. Note that for each acceptable branch x,
$i(x)\supseteq [n,\infty )$
is called the degree of acceptability of x. Note that for each acceptable branch x,
![]() $y_x=\{k(i+1)\colon i\in i(x)\}\in \operatorname {\mathrm {fil}}(\mathcal {A})$
. Moreover, each
$y_x=\{k(i+1)\colon i\in i(x)\}\in \operatorname {\mathrm {fil}}(\mathcal {A})$
. Moreover, each
![]() $s\in p$
can be extended to an acceptable branch. Indeed, if
$s\in p$
can be extended to an acceptable branch. Indeed, if
![]() $s\in \operatorname {\mathrm {split}}_l(p)$
, take j such that
$s\in \operatorname {\mathrm {split}}_l(p)$
, take j such that
![]() $l\leq k(j)$
. Thus, we assume that
$l\leq k(j)$
. Thus, we assume that
![]() $k(j+1)\in Y_s$
. By part (iv) of Claim 4.2 there is
$k(j+1)\in Y_s$
. By part (iv) of Claim 4.2 there is
![]() $t\in \operatorname {\mathrm {split}}_{k(j+1)}(p)$
extending s such that
$t\in \operatorname {\mathrm {split}}_{k(j+1)}(p)$
extending s such that
![]() $p(t)\Vdash \check {k}(j+1)\in \dot {Y}$
. Repeat the procedure recursively to build an acceptable branch extending s. In the following, we continue using a fusion argument. We build a fusion sequence
$p(t)\Vdash \check {k}(j+1)\in \dot {Y}$
. Repeat the procedure recursively to build an acceptable branch extending s. In the following, we continue using a fusion argument. We build a fusion sequence
![]() $\{(p_n,X_n)\}_{n\in \omega }$
.
$\{(p_n,X_n)\}_{n\in \omega }$
.
To define
![]() $p_0$
, take some acceptable branch x extending some node in
$p_0$
, take some acceptable branch x extending some node in
![]() $\operatorname {\mathrm {split}}_{k(0)+1}(p)$
with degree of acceptability at most
$\operatorname {\mathrm {split}}_{k(0)+1}(p)$
with degree of acceptability at most
![]() $0$
, and a node
$0$
, and a node
![]() $s=x\restriction \operatorname {\mathrm {split}}_{k(1)}(p)$
. We set
$s=x\restriction \operatorname {\mathrm {split}}_{k(1)}(p)$
. We set
![]() $p_0=p(s)$
and
$p_0=p(s)$
and
![]() $X_0=\{x\}$
.
$X_0=\{x\}$
.
Let us assume that
![]() $p_n$
and
$p_n$
and
![]() $X_n$
are defined, and consider
$X_n$
are defined, and consider
![]() $s\in \operatorname {\mathrm {split}}_{k(n)}(p)\cap \operatorname {\mathrm {split}}(p_n)$
. Take the unique acceptable branch
$s\in \operatorname {\mathrm {split}}_{k(n)}(p)\cap \operatorname {\mathrm {split}}(p_n)$
. Take the unique acceptable branch
![]() $x\in X_n$
extending s. Define
$x\in X_n$
extending s. Define
![]() $i=x(|s|)\in \{0,1\}$
and
$i=x(|s|)\in \{0,1\}$
and
![]() $s_i=x\restriction \operatorname {\mathrm {split}}_{k(n+1)}(p)$
. Then we set
$s_i=x\restriction \operatorname {\mathrm {split}}_{k(n+1)}(p)$
. Then we set
![]() $s_{1-i}$
to be an extension of
$s_{1-i}$
to be an extension of
![]() $s^{\smallfrown }\langle {1-i}\rangle $
such that:
$s^{\smallfrown }\langle {1-i}\rangle $
such that:
-
(i)
 $[p(s_{1-i})]\cap C_{\alpha _x}=\emptyset $
for all already considered acceptable branches x (i.e., all branches in
$[p(s_{1-i})]\cap C_{\alpha _x}=\emptyset $
for all already considered acceptable branches x (i.e., all branches in
 $X_n$
and those assigned to previous nodes in some order of
$X_n$
and those assigned to previous nodes in some order of
 $\operatorname {\mathrm {split}}_{k(n)}(p)\cap \operatorname {\mathrm {split}}(p_n)$
). This can be easily achieved since each
$\operatorname {\mathrm {split}}_{k(n)}(p)\cap \operatorname {\mathrm {split}}(p_n)$
). This can be easily achieved since each
 $C_{\alpha _x}$
is nowhere dense in
$C_{\alpha _x}$
is nowhere dense in
 $[p]$
.
$[p]$
. -
(ii)
 $s_{1-i}=x\restriction \operatorname {\mathrm {split}}_{k(j+1)}(p)$
with
$s_{1-i}=x\restriction \operatorname {\mathrm {split}}_{k(j+1)}(p)$
with
 $j\in i(x)$
for some acceptable branch
$j\in i(x)$
for some acceptable branch
 $x\in [p]$
with degree of acceptability at most j. Let us recall that each node can be extended to an acceptable branch.
$x\in [p]$
with degree of acceptability at most j. Let us recall that each node can be extended to an acceptable branch.
Finally, let
![]() $X_{n+1}$
be the set of all considered acceptable branches in this step, and
$X_{n+1}$
be the set of all considered acceptable branches in this step, and
One can see that the sequence
![]() $\{(p_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses. Let
$\{(p_n,X_n)\}_{n\in \omega }$
is a fusion sequence with witnesses. Let
![]() $q=\bigcap \{p_n\colon n\in \omega \}$
and let
$q=\bigcap \{p_n\colon n\in \omega \}$
and let
![]() $X=\bigcup \{X_n\colon n\in \omega \}$
.
$X=\bigcup \{X_n\colon n\in \omega \}$
.
We shall show that the family
![]() $\{y_x\colon x\in X\}$
possesses the desired properties. Indeed, let
$\{y_x\colon x\in X\}$
possesses the desired properties. Indeed, let
![]() $x\in X$
. For each
$x\in X$
. For each
![]() $n\in \omega $
we have
$n\in \omega $
we have
![]() $y_x(n)=k(i(x)(n)+1)$
. Due to construction of q we have
$y_x(n)=k(i(x)(n)+1)$
. Due to construction of q we have
![]() $x\restriction \operatorname {\mathrm {split}}_n(q)=x\restriction \operatorname {\mathrm {split}}_{k(j_n+1)}(p)$
for some increasing sequence
$x\restriction \operatorname {\mathrm {split}}_n(q)=x\restriction \operatorname {\mathrm {split}}_{k(j_n+1)}(p)$
for some increasing sequence
![]() $\{j_i\}_{i\in \omega }$
, and if
$\{j_i\}_{i\in \omega }$
, and if
![]() $t=x\restriction \operatorname {\mathrm {split}}_n(q)$
then
$t=x\restriction \operatorname {\mathrm {split}}_n(q)$
then
![]() $p(t)\Vdash \check {k}(j_n+1)\in \dot {Y}$
. Thus
$p(t)\Vdash \check {k}(j_n+1)\in \dot {Y}$
. Thus
![]() $k(j_n+1)\in y_x$
and consequently
$k(j_n+1)\in y_x$
and consequently
![]() $j_n\geq i(x)(n)$
for each n. Let us now fix n and consider
$j_n\geq i(x)(n)$
for each n. Let us now fix n and consider
![]() $t=x\restriction \operatorname {\mathrm {split}}_n(q)$
. The definition of
$t=x\restriction \operatorname {\mathrm {split}}_n(q)$
. The definition of
![]() $y_x$
guarantees that
$y_x$
guarantees that
![]() $p(s)\Vdash \check {k}(i(x)(n)+1)\in \dot {Y}$
for
$p(s)\Vdash \check {k}(i(x)(n)+1)\in \dot {Y}$
for
![]() $s=x\restriction \operatorname {\mathrm {split}}_{k(i(x)(n)+1)}(p)$
. Thus we have
$s=x\restriction \operatorname {\mathrm {split}}_{k(i(x)(n)+1)}(p)$
. Thus we have
![]() $q(s)\Vdash \check {y}_x(n)\in \dot {Y}$
. On the other hand,
$q(s)\Vdash \check {y}_x(n)\in \dot {Y}$
. On the other hand,
![]() $s=x\restriction \operatorname {\mathrm {split}}_{k(i(x)(n)+1)}(p)\subseteq x\restriction \operatorname {\mathrm {split}}_{k(j_n+1)}(p)=x\restriction \operatorname {\mathrm {split}}_n(q)=t$
.
$s=x\restriction \operatorname {\mathrm {split}}_{k(i(x)(n)+1)}(p)\subseteq x\restriction \operatorname {\mathrm {split}}_{k(j_n+1)}(p)=x\restriction \operatorname {\mathrm {split}}_n(q)=t$
.
The last part of our proof resembles the proof of the previous claim. Let
![]() $x_s$
for
$x_s$
for
![]() $s\in \operatorname {\mathrm {split}}(p)$
be the branch in X extending s such that if
$s\in \operatorname {\mathrm {split}}(p)$
be the branch in X extending s such that if
![]() $s\subseteq t\subseteq x_s$
then
$s\subseteq t\subseteq x_s$
then
![]() $x_t=x_s$
. The corresponding
$x_t=x_s$
. The corresponding
![]() $y_{x_s}$
is denoted by
$y_{x_s}$
is denoted by
![]() $y_s$
. The set
$y_s$
. The set
![]() $y_s$
belongs to
$y_s$
belongs to
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
. By Lemma 3.9 for
$\operatorname {\mathrm {fil}}(\mathcal {A})\cap V$
. By Lemma 3.9 for
![]() $\mathcal {G}_n$
being the family of all
$\mathcal {G}_n$
being the family of all
![]() $y_t$
’s with
$y_t$
’s with
![]() $t\in \operatorname {\mathrm {split}}_{\leq n}(p)$
, we obtain
$t\in \operatorname {\mathrm {split}}_{\leq n}(p)$
, we obtain
![]() $\{l(n)\colon n\in \omega \}\in \operatorname {\mathrm {fil}}(\mathcal {A})$
such that
$\{l(n)\colon n\in \omega \}\in \operatorname {\mathrm {fil}}(\mathcal {A})$
such that
Let us denote
![]() $C=\{l(n+1)\colon n\in \omega \}$
. We shall construct a condition
$C=\{l(n+1)\colon n\in \omega \}$
. We shall construct a condition
![]() $q^*\leq p$
such that
$q^*\leq p$
such that
![]() $q^*\Vdash \check {C}\subseteq \dot {Y}$
. Then
$q^*\Vdash \check {C}\subseteq \dot {Y}$
. Then
![]() $q^*\Vdash \dot {Y}\in \operatorname {\mathrm {fil}}(\mathcal {A})$
which is a contradiction.
$q^*\Vdash \dot {Y}\in \operatorname {\mathrm {fil}}(\mathcal {A})$
which is a contradiction.
We build a fusion sequence
![]() $\{(p_n,X_n)\}_{n\in \omega }$
. Let
$\{(p_n,X_n)\}_{n\in \omega }$
. Let
![]() $p_0=p$
,
$p_0=p$
,
![]() $X_0=\{x_t\}$
for
$X_0=\{x_t\}$
for
![]() $t\in \operatorname {\mathrm {split}}_0(p)$
, and suppose we have defined
$t\in \operatorname {\mathrm {split}}_0(p)$
, and suppose we have defined
![]() $p_n$
. For each
$p_n$
. For each
![]() $t\in \operatorname {\mathrm {split}}_n(p_n)\subseteq \operatorname {\mathrm {split}}_{l(n)}(p)$
and each
$t\in \operatorname {\mathrm {split}}_n(p_n)\subseteq \operatorname {\mathrm {split}}_{l(n)}(p)$
and each
![]() $i\in \{0,1\}$
take
$i\in \{0,1\}$
take
![]() $w^*(t,i)\in \operatorname {\mathrm {split}}_{l(n)+1}(p)$
such that
$w^*(t,i)\in \operatorname {\mathrm {split}}_{l(n)+1}(p)$
such that
![]() $w^*(t,i)$
end-extends
$w^*(t,i)$
end-extends
![]() $t^{\smallfrown } i$
. Then
$t^{\smallfrown } i$
. Then
and so for each
![]() $t,i$
we take
$t,i$
we take
![]() $w(t,i)=x_{w^*(t,i)}\restriction \operatorname {\mathrm {split}}_{l(n+1)}(p)$
. Note that by Claim 4.3 and the fact that
$w(t,i)=x_{w^*(t,i)}\restriction \operatorname {\mathrm {split}}_{l(n+1)}(p)$
. Note that by Claim 4.3 and the fact that
![]() $l(n+1)\geq j$
for
$l(n+1)\geq j$
for
![]() $l(n+1)=y_{w^*(t,i)}(j)$
we obtain
$l(n+1)=y_{w^*(t,i)}(j)$
we obtain
Take
![]() $p_{n+1}\kern1.2pt{=}\kern1.2pt\bigcup \{p(w(t,i))\colon t\kern1.2pt{\in}\kern1.2pt \operatorname {\mathrm {split}}_n(p_n), i\kern1.2pt{\in}\kern1.2pt \{0,1\}\}$
,
$p_{n+1}\kern1.2pt{=}\kern1.2pt\bigcup \{p(w(t,i))\colon t\kern1.2pt{\in}\kern1.2pt \operatorname {\mathrm {split}}_n(p_n), i\kern1.2pt{\in}\kern1.2pt \{0,1\}\}$
,
![]() $X_{n+1}\kern1.2pt{=}\kern1.2pt\{x_{w(t,i)}\colon t\kern1.2pt{\in}\kern1.2pt \operatorname {\mathrm {split}}_n(p_n), i\in \{0,1\}\}$
. Finally, let
$X_{n+1}\kern1.2pt{=}\kern1.2pt\{x_{w(t,i)}\colon t\kern1.2pt{\in}\kern1.2pt \operatorname {\mathrm {split}}_n(p_n), i\in \{0,1\}\}$
. Finally, let
![]() $q^*$
be the fusion of
$q^*$
be the fusion of
![]() $\{(p_n,X_n)\}_{n\in \omega }$
. Then, since
$\{(p_n,X_n)\}_{n\in \omega }$
. Then, since
![]() $q^*\Vdash l(n+1)\in \dot {Y}$
for all
$q^*\Vdash l(n+1)\in \dot {Y}$
for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $q^*$
is as required.
$q^*$
is as required.
4.2 Laflamme’s filter game
We give yet one more proof of the fact that Miller partition forcing preserves selective independent families, which is based on Laflamme’s filter game. We will make use of the following property, which can be deduced from [Reference Zapletal52, Propositions 4.1.2 and 4.1.31].
Lemma 4.4. Let
![]() $p\in \mathbb {Q}(\mathcal {C})$
and let
$p\in \mathbb {Q}(\mathcal {C})$
and let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbb {Q}(\mathcal {C})$
-name such that
$\mathbb {Q}(\mathcal {C})$
-name such that
![]() $p\Vdash \dot {f}\in 2^{\omega }$
. Then there exists
$p\Vdash \dot {f}\in 2^{\omega }$
. Then there exists
![]() $q\leq p$
and a continuous
$q\leq p$
and a continuous
![]() $H:[q]\longrightarrow 2^{\omega }$
such that
$H:[q]\longrightarrow 2^{\omega }$
such that
![]() $q\Vdash H(\dot {r}_{gen})=\dot {f}$
.
$q\Vdash H(\dot {r}_{gen})=\dot {f}$
.
Definition 4.5 (Laflamme [Reference Laflamme34]).
Let
![]() $\mathcal {F}$
be a filter over
$\mathcal {F}$
be a filter over
![]() $\omega $
. The game
$\omega $
. The game
![]() $\mathfrak {G}(\mathcal {F},\omega ,\mathcal {F})$
is defined as follows. On the n turn, Player I plays some
$\mathfrak {G}(\mathcal {F},\omega ,\mathcal {F})$
is defined as follows. On the n turn, Player I plays some
![]() $U_n\in \mathcal {F}$
and Player II responds with some
$U_n\in \mathcal {F}$
and Player II responds with some
![]() $a_n\in U_n$
. After
$a_n\in U_n$
. After
![]() $\omega $
turns, Player II wins if the sequence
$\omega $
turns, Player II wins if the sequence
![]() $\{a_n\}_{n\in \omega }$
belongs to
$\{a_n\}_{n\in \omega }$
belongs to
![]() $\mathcal {F}.$
Otherwise, Player I wins.
$\mathcal {F}.$
Otherwise, Player I wins.
It is not hard to prove that Player II never has a winning strategy in this game. On the other hand, we have the following theorem of Laflamme, see [Reference Laflamme34] (as well as [Reference Laflamme and Leary35]).
Theorem 4.6 (Laflamme).
A filter
![]() $\mathcal {F}$
is not selective if and only if Player I does have a winning strategy for the game
$\mathcal {F}$
is not selective if and only if Player I does have a winning strategy for the game
![]() $\mathfrak {G}(\mathcal {F},\omega ,\mathcal {F})$
.
$\mathfrak {G}(\mathcal {F},\omega ,\mathcal {F})$
.
Lemma 4.7. Let
![]() $\mathcal {F}$
be a selective filter,
$\mathcal {F}$
be a selective filter,
![]() $p\in \mathbb {S}$
, and
$p\in \mathbb {S}$
, and
![]() $H:[p]\longrightarrow P(\omega )$
be a continuous function such that for every
$H:[p]\longrightarrow P(\omega )$
be a continuous function such that for every
![]() $s\in p$
,
$s\in p$
,
Then there are
![]() $q\in \mathbb {S}$
,
$q\in \mathbb {S}$
,
![]() $Y\in \mathcal {F}$
such that
$Y\in \mathcal {F}$
such that
![]() $q\subseteq p$
and for every
$q\subseteq p$
and for every
![]() $f\in [q]$
,
$f\in [q]$
,
![]() $Y\subseteq H(f)$
.
$Y\subseteq H(f)$
.
Proof For every
![]() $q\in \mathbb {S}$
such that
$q\in \mathbb {S}$
such that
![]() $q\subseteq p$
, let
$q\subseteq p$
, let
![]() $L(q)=\bigcup H\big [[q]\big ]$
. Now consider the game
$L(q)=\bigcup H\big [[q]\big ]$
. Now consider the game
![]() $\mathfrak {G}(\mathcal {F},\omega ,\mathcal {F})$
. Player I will play the following strategy, while constructing a sequence
$\mathfrak {G}(\mathcal {F},\omega ,\mathcal {F})$
. Player I will play the following strategy, while constructing a sequence
![]() $\{t_{\sigma }\}_{\sigma \in 2^{<\omega }}\subseteq p$
such that:
$\{t_{\sigma }\}_{\sigma \in 2^{<\omega }}\subseteq p$
such that:
-
(a)
 $\forall \sigma \in 2^{<\omega } \forall i\in 2\big (t_{\sigma }\subsetneq t_{\sigma ^{\smallfrown } i}\big ).$
$\forall \sigma \in 2^{<\omega } \forall i\in 2\big (t_{\sigma }\subsetneq t_{\sigma ^{\smallfrown } i}\big ).$
-
(b)
 $\forall \sigma ,\tau \in 2^n\big (\sigma \not =\tau \rightarrow (t_{\sigma } \text { and } t_{\tau } \text { are incomparable })\big ).$
$\forall \sigma ,\tau \in 2^n\big (\sigma \not =\tau \rightarrow (t_{\sigma } \text { and } t_{\tau } \text { are incomparable })\big ).$
On the first turn Player I defines
![]() $t_{\emptyset }=\emptyset $
and plays
$t_{\emptyset }=\emptyset $
and plays
![]() $U_0=L(p(t_{\emptyset }))$
. As the rules dictate, Player II responds with some
$U_0=L(p(t_{\emptyset }))$
. As the rules dictate, Player II responds with some
![]() $a_0\in U_0$
. Since
$a_0\in U_0$
. Since
![]() $a_0\in \bigcup H\big [[p(t_{\emptyset })]\big ]$
, there is
$a_0\in \bigcup H\big [[p(t_{\emptyset })]\big ]$
, there is
![]() $f\in [p(t_{\emptyset })]$
such that
$f\in [p(t_{\emptyset })]$
such that
![]() $a_0\in H(f)$
. As H is continuous there is
$a_0\in H(f)$
. As H is continuous there is
![]() $k\in \omega $
such that for every
$k\in \omega $
such that for every
![]() $g\in [p(f|_k)]$
we have
$g\in [p(f|_k)]$
we have
![]() $a_0\in H(g)$
. Now Player I extends
$a_0\in H(g)$
. Now Player I extends
![]() $f|_k$
to incomparable
$f|_k$
to incomparable
![]() $t_0,t_1\in p$
such that
$t_0,t_1\in p$
such that
![]() $t_{\emptyset }\subsetneq t_0,t_1$
and plays
$t_{\emptyset }\subsetneq t_0,t_1$
and plays
![]() $U_1=L(p(t_0))\cap L(p(t_1))$
. As the rules dictate Player II responds with some
$U_1=L(p(t_0))\cap L(p(t_1))$
. As the rules dictate Player II responds with some
![]() $a_1\in U_1$
.
$a_1\in U_1$
.
In general, suppose that it is the
![]() $n+1$
turn and that Player I has constructed
$n+1$
turn and that Player I has constructed
![]() $\{t_{\sigma }\}_{\sigma \in 2^{\leq n}}$
and for every
$\{t_{\sigma }\}_{\sigma \in 2^{\leq n}}$
and for every
![]() $m\leq n$
played
$m\leq n$
played
![]() $U_m=\bigcap \limits _{\sigma \in 2^{\leq m}} L(p(t_{\sigma }))$
. As
$U_m=\bigcap \limits _{\sigma \in 2^{\leq m}} L(p(t_{\sigma }))$
. As
![]() $a_n\in \bigcap \limits _{\sigma \in 2^n}\big (\bigcup H\big [[p(t_{\sigma })]\big ]\big ) $
, for every
$a_n\in \bigcap \limits _{\sigma \in 2^n}\big (\bigcup H\big [[p(t_{\sigma })]\big ]\big ) $
, for every
![]() $\sigma \in 2^n$
there is
$\sigma \in 2^n$
there is
![]() $f_{\sigma }\in [p(t_0)]$
such that
$f_{\sigma }\in [p(t_0)]$
such that
![]() $a_n\in H(f_{\sigma }).$
Since H is continuous, there is
$a_n\in H(f_{\sigma }).$
Since H is continuous, there is
![]() $k\in \omega $
such that for every
$k\in \omega $
such that for every
![]() $\sigma \in 2^n$
and every
$\sigma \in 2^n$
and every
![]() $g\in [p(f_{\sigma }|_k)], a_n\in H(g)$
. Now Player I extends each
$g\in [p(f_{\sigma }|_k)], a_n\in H(g)$
. Now Player I extends each
![]() $f_{\sigma }|_k$
to incomparable
$f_{\sigma }|_k$
to incomparable
![]() $t_{\sigma ^{\smallfrown } 0},t_{\sigma ^{\smallfrown } 1}\in p$
such that
$t_{\sigma ^{\smallfrown } 0},t_{\sigma ^{\smallfrown } 1}\in p$
such that
![]() $t_{\sigma } \subsetneq t_{\sigma ^{\smallfrown } 0},t_{\sigma ^{\smallfrown } 1}$
and plays
$t_{\sigma } \subsetneq t_{\sigma ^{\smallfrown } 0},t_{\sigma ^{\smallfrown } 1}$
and plays
![]() $U_{n+1}=\bigcap \limits _{\sigma \in 2^{\leq {n+1}}} L(p(t_{\sigma }))$
. As the rules dictate, Player II responds with some
$U_{n+1}=\bigcap \limits _{\sigma \in 2^{\leq {n+1}}} L(p(t_{\sigma }))$
. As the rules dictate, Player II responds with some
![]() $a_{n+1}\in U_{n+1}$
.
$a_{n+1}\in U_{n+1}$
.
Since
![]() $\mathcal {F}$
is a selective filter, this is not a winning strategy for Player I. Therefore there is a match where Player I plays by the above strategy, but Player II wins. Let
$\mathcal {F}$
is a selective filter, this is not a winning strategy for Player I. Therefore there is a match where Player I plays by the above strategy, but Player II wins. Let
![]() $\{a_n\}_{n\in \omega }$
and
$\{a_n\}_{n\in \omega }$
and
![]() $\{t_{\sigma }\}_{\sigma \in 2^{<\omega }}$
be the sequences associated with one of these matches and let
$\{t_{\sigma }\}_{\sigma \in 2^{<\omega }}$
be the sequences associated with one of these matches and let
![]() $q=\{\tau \in p\;|\;\exists \sigma \in 2^{<\omega }\big (\tau \subseteq t_{\sigma }\big )\}$
. It is straightforward that q and
$q=\{\tau \in p\;|\;\exists \sigma \in 2^{<\omega }\big (\tau \subseteq t_{\sigma }\big )\}$
. It is straightforward that q and
![]() $Y=\{a_n\}_{n\in \omega }$
are the objects we are looking for.
$Y=\{a_n\}_{n\in \omega }$
are the objects we are looking for.
Theorem 4.8. Let
![]() $\mathcal {F}$
be a selective filter and let G be a
$\mathcal {F}$
be a selective filter and let G be a
![]() $\mathbb {Q}(\mathcal {C})$
-generic filter. In
$\mathbb {Q}(\mathcal {C})$
-generic filter. In
![]() $V[G]$
, for every
$V[G]$
, for every
![]() $X\in P(\omega )$
one of the following statements occurs:
$X\in P(\omega )$
one of the following statements occurs:
-
(a) There is
 $Y\in \mathcal {F}\cap V$
such that
$Y\in \mathcal {F}\cap V$
such that
 $Y\subseteq X$
.
$Y\subseteq X$
. -
(b) There is
 $Z\in V$
, such that
$Z\in V$
, such that
 $Z\notin \mathcal {F}$
and
$Z\notin \mathcal {F}$
and
 $X\subseteq Z$
.
$X\subseteq Z$
.
Proof Let
![]() $\dot {X}$
be a name for a subset of
$\dot {X}$
be a name for a subset of
![]() $\omega $
,
$\omega $
,
![]() $p\in \mathbb {Q}(\mathcal {C})$
, and suppose no condition below p forces
$p\in \mathbb {Q}(\mathcal {C})$
, and suppose no condition below p forces
![]() $(b)$
. By Lemma 4.4 there is a continuous
$(b)$
. By Lemma 4.4 there is a continuous
![]() $H:[p]\longrightarrow P(\omega )$
such that
$H:[p]\longrightarrow P(\omega )$
such that
![]() $p\Vdash H(\dot {r}_{gen})=\dot {X}$
. For every
$p\Vdash H(\dot {r}_{gen})=\dot {X}$
. For every
![]() $q\in \mathbb {S}$
such that
$q\in \mathbb {S}$
such that
![]() $q\subseteq p$
, let
$q\subseteq p$
, let
![]() $L(q)=\bigcup H\big [[q]\big ]$
and note that if
$L(q)=\bigcup H\big [[q]\big ]$
and note that if
![]() $q\in \mathbb {Q}(\mathcal {C})$
then
$q\in \mathbb {Q}(\mathcal {C})$
then
![]() $L(q)\in \mathcal {F}$
. This holds, because
$L(q)\in \mathcal {F}$
. This holds, because
![]() $q\Vdash \dot {X}\subseteq L(q)$
and q does not force
$q\Vdash \dot {X}\subseteq L(q)$
and q does not force
![]() $(b)$
. We say that a condition
$(b)$
. We say that a condition
![]() $q\in \mathbb {S}$
, which is not necessarily in
$q\in \mathbb {S}$
, which is not necessarily in
![]() $\mathbb {Q}(\mathcal {C})$
, is special if
$\mathbb {Q}(\mathcal {C})$
, is special if
![]() $q\subseteq p$
and for every
$q\subseteq p$
and for every
![]() $s\in q$
we have that
$s\in q$
we have that
![]() $L(q(s))\in \mathcal {F}$
.
$L(q(s))\in \mathcal {F}$
.
We will make use of the following notion: Given
![]() $s\in p$
we say that the pair
$s\in p$
we say that the pair
![]() $(q,T)$
is s-special if
$(q,T)$
is s-special if
![]() $q\in \mathbb {S}$
is special,
$q\in \mathbb {S}$
is special,
![]() $T\in \mathcal {C}$
,
$T\in \mathcal {C}$
,
![]() $[q]\subseteq [p(s)]\cap T$
. We divide the proof in cases.
$[q]\subseteq [p(s)]\cap T$
. We divide the proof in cases.
Case 1. For every
![]() $s\in p$
, there is an s-special pair
$s\in p$
, there is an s-special pair
![]() $(q,T)$
.
$(q,T)$
.
In this case, consider the game
![]() $\mathfrak {G}(\mathcal {F},\omega ,\mathcal {F})$
. Player I will play by the following strategy, while recursively constructing sequences
$\mathfrak {G}(\mathcal {F},\omega ,\mathcal {F})$
. Player I will play by the following strategy, while recursively constructing sequences
![]() $\{q_{\sigma }\}_{\sigma \in 2^{<\omega }}\subseteq \mathbb {S}$
,
$\{q_{\sigma }\}_{\sigma \in 2^{<\omega }}\subseteq \mathbb {S}$
,
![]() $\{s_{\sigma }\}_{\sigma \in 2^{<\omega }}\subseteq p$
, and
$\{s_{\sigma }\}_{\sigma \in 2^{<\omega }}\subseteq p$
, and
![]() $\{T_{\sigma }\}_{\sigma \in 2^{<\omega }}\subseteq \mathcal {C}$
such that:
$\{T_{\sigma }\}_{\sigma \in 2^{<\omega }}\subseteq \mathcal {C}$
such that:
-
(a)
 $\forall \sigma \in 2^{<\omega }$
the pair
$\forall \sigma \in 2^{<\omega }$
the pair
 $(q_{\sigma },T_{\sigma })$
is
$(q_{\sigma },T_{\sigma })$
is
 $s_{\sigma }$
-special;
$s_{\sigma }$
-special; -
(b)
 $\forall \sigma \in 2^{<\omega }\big (q_{\sigma ^{\smallfrown } 0}\subseteq q_{\sigma }\big )$
;
$\forall \sigma \in 2^{<\omega }\big (q_{\sigma ^{\smallfrown } 0}\subseteq q_{\sigma }\big )$
; -
(c)
 $\forall \sigma \in 2^{<\omega }\big (T_{\sigma ^{\smallfrown } 0}= T_{\sigma }\big )$
;
$\forall \sigma \in 2^{<\omega }\big (T_{\sigma ^{\smallfrown } 0}= T_{\sigma }\big )$
; -
(d)
 $\forall \sigma ,\tau \in 2^n\big (\sigma \not =\tau \rightarrow T_{\sigma }\not =T_{\tau }\big )$
;
$\forall \sigma ,\tau \in 2^n\big (\sigma \not =\tau \rightarrow T_{\sigma }\not =T_{\tau }\big )$
; -
(e)
 $\forall \sigma \in 2^{<\omega }\forall i\in 2\big (s_{\sigma }\subsetneq s_{\sigma ^{\smallfrown } i}\big )$
;
$\forall \sigma \in 2^{<\omega }\forall i\in 2\big (s_{\sigma }\subsetneq s_{\sigma ^{\smallfrown } i}\big )$
; -
(f)
 $\forall \sigma \in 2^{<\omega }\big ( s_{\sigma ^{\smallfrown } 0}\in q_{\sigma } \wedge [p( s_{\sigma ^{\smallfrown } 1})]\cap T_{\sigma }=\emptyset \big )$
.
$\forall \sigma \in 2^{<\omega }\big ( s_{\sigma ^{\smallfrown } 0}\in q_{\sigma } \wedge [p( s_{\sigma ^{\smallfrown } 1})]\cap T_{\sigma }=\emptyset \big )$
.
On the first turn, Player I defines
![]() $s_{\emptyset }=\emptyset $
, an
$s_{\emptyset }=\emptyset $
, an
![]() $s_{\emptyset }$
-special pair
$s_{\emptyset }$
-special pair
![]() $(q_{\emptyset },T_{\emptyset })$
and plays
$(q_{\emptyset },T_{\emptyset })$
and plays
![]() $U_0=L(q_{\emptyset })$
. As the rules dictate, Player II responds with some
$U_0=L(q_{\emptyset })$
. As the rules dictate, Player II responds with some
![]() $a_0\in U_0$
. Since
$a_0\in U_0$
. Since
![]() $a_0\in \bigcup H\big [[q_{\emptyset }]\big ]$
, there is some
$a_0\in \bigcup H\big [[q_{\emptyset }]\big ]$
, there is some
![]() $f\in [q_{\emptyset }]$
such that
$f\in [q_{\emptyset }]$
such that
![]() $a_0\in H(f)$
and since H is continuous there is
$a_0\in H(f)$
and since H is continuous there is
![]() $k\in \omega $
such that for every
$k\in \omega $
such that for every
![]() $g\in [p(f|_k)]$
,
$g\in [p(f|_k)]$
,
![]() $a_0\in H(g)$
. Notice that since
$a_0\in H(g)$
. Notice that since
![]() $(q_{\emptyset },T_{\emptyset })$
is
$(q_{\emptyset },T_{\emptyset })$
is
![]() $s_{\emptyset }$
-special, we have that
$s_{\emptyset }$
-special, we have that
![]() $f|_k$
is compatible with
$f|_k$
is compatible with
![]() $s_{\emptyset }$
and moreover we can extend
$s_{\emptyset }$
and moreover we can extend
![]() $f|_k$
to incomparable
$f|_k$
to incomparable
![]() $s_0,s_1\in p$
such that
$s_0,s_1\in p$
such that
![]() $s_{\emptyset }\subsetneq s_0,s_1$
,
$s_{\emptyset }\subsetneq s_0,s_1$
,
![]() $s_0\in q_{\emptyset }$
and
$s_0\in q_{\emptyset }$
and
![]() $[p(s_1)]\cap T_{\emptyset }=\emptyset $
. Now Player I defines
$[p(s_1)]\cap T_{\emptyset }=\emptyset $
. Now Player I defines
![]() $q_0=q_{\emptyset }(s_0)$
,
$q_0=q_{\emptyset }(s_0)$
,
![]() $T_0=T_{\emptyset }$
, an
$T_0=T_{\emptyset }$
, an
![]() $s_1$
-special pair
$s_1$
-special pair
![]() $(q_1, T_1)$
and plays
$(q_1, T_1)$
and plays
![]() $U_1= L(q_0)\cap L(q_1)$
. As the rules dictate, Player II responds with some
$U_1= L(q_0)\cap L(q_1)$
. As the rules dictate, Player II responds with some
![]() $a_1\in U_1$
.
$a_1\in U_1$
.
In general, suppose that it is the
![]() $n+1$
turn and Player I has constructed
$n+1$
turn and Player I has constructed
![]() $q_{\sigma }, s_{\sigma }$
, and
$q_{\sigma }, s_{\sigma }$
, and
![]() $T_{\sigma }$
for every
$T_{\sigma }$
for every
![]() $\sigma \in 2^{\leq n}$
. Moreover, suppose that for every
$\sigma \in 2^{\leq n}$
. Moreover, suppose that for every
![]() $m\leq n$
Player I has played
$m\leq n$
Player I has played
![]() $U_m=\bigcap \limits _{\sigma \in 2^m}L(q_{\sigma })$
. Since
$U_m=\bigcap \limits _{\sigma \in 2^m}L(q_{\sigma })$
. Since
![]() $a_n \in \bigcap \limits _{\sigma \in 2^n}\big (\bigcup H\big [[q_{\sigma }]\big ]\big )$
, for every
$a_n \in \bigcap \limits _{\sigma \in 2^n}\big (\bigcup H\big [[q_{\sigma }]\big ]\big )$
, for every
![]() $\sigma \in 2^n$
there is
$\sigma \in 2^n$
there is
![]() $f_{\sigma }\in [q_{\sigma }]$
such that
$f_{\sigma }\in [q_{\sigma }]$
such that
![]() $a_n\in H(f_{\sigma })$
. As H is continuous, there is
$a_n\in H(f_{\sigma })$
. As H is continuous, there is
![]() $k\in \omega $
such that for every
$k\in \omega $
such that for every
![]() $\sigma \in 2^n$
and every
$\sigma \in 2^n$
and every
![]() $g\in [p(f_{\sigma }|_k)]$
,
$g\in [p(f_{\sigma }|_k)]$
,
![]() $a_n\in H(g)$
. As each
$a_n\in H(g)$
. As each
![]() $(q_{\sigma },T_{\sigma })$
is
$(q_{\sigma },T_{\sigma })$
is
![]() $s_{\sigma }$
-special, we have that
$s_{\sigma }$
-special, we have that
![]() $f_{\sigma }|_k$
is compatible with
$f_{\sigma }|_k$
is compatible with
![]() $s_{\sigma }$
and that
$s_{\sigma }$
and that
![]() $\bigcup \limits _{\sigma \in 2^n} T_{\sigma }\cap [p]$
is nowhere dense in
$\bigcup \limits _{\sigma \in 2^n} T_{\sigma }\cap [p]$
is nowhere dense in
![]() $[p]$
. Then we can extend each
$[p]$
. Then we can extend each
![]() $f_{\sigma }|_k$
to incomparable
$f_{\sigma }|_k$
to incomparable
![]() $s_{\sigma ^{\smallfrown } 0},s_{\sigma ^{\smallfrown } 1}\in p$
such that
$s_{\sigma ^{\smallfrown } 0},s_{\sigma ^{\smallfrown } 1}\in p$
such that
![]() $s_{\sigma }\subsetneq s_{\sigma ^{\smallfrown } 0}$
,
$s_{\sigma }\subsetneq s_{\sigma ^{\smallfrown } 0}$
,
![]() $s_{\sigma ^{\smallfrown } 1}$
,
$s_{\sigma ^{\smallfrown } 1}$
,
![]() $s_{\sigma ^{\smallfrown } 0}\in q_{\sigma }$
and
$s_{\sigma ^{\smallfrown } 0}\in q_{\sigma }$
and
![]() $[p( s_{\sigma ^{\smallfrown } 1})]\cap T_{\sigma }=\emptyset $
. Now Player I defines
$[p( s_{\sigma ^{\smallfrown } 1})]\cap T_{\sigma }=\emptyset $
. Now Player I defines
![]() $q_{\sigma ^{\smallfrown } 0}=q_{\sigma }(s_{\sigma ^{\smallfrown } 0})$
,
$q_{\sigma ^{\smallfrown } 0}=q_{\sigma }(s_{\sigma ^{\smallfrown } 0})$
,
![]() $T_{\sigma \smallfrown 0}=T_{\sigma }$
, an
$T_{\sigma \smallfrown 0}=T_{\sigma }$
, an
![]() $s_{\sigma ^{\smallfrown } 1}$
-special pair
$s_{\sigma ^{\smallfrown } 1}$
-special pair
![]() $(q_{\sigma ^{\smallfrown } 1},T_{\sigma ^{\smallfrown } 1})$
and plays
$(q_{\sigma ^{\smallfrown } 1},T_{\sigma ^{\smallfrown } 1})$
and plays
![]() $U_{n+1}=\bigcap \limits _{\sigma \in 2^{n+1}}L(q_{\sigma })$
. As the rules dictate, Player II responds with some
$U_{n+1}=\bigcap \limits _{\sigma \in 2^{n+1}}L(q_{\sigma })$
. As the rules dictate, Player II responds with some
![]() $a_{n+1}\in U_{n+1}$
.
$a_{n+1}\in U_{n+1}$
.
Since
![]() $\mathcal {F}$
is a selective filter, the above is not a winning strategy for Player I and so, there is a match where Player I follows the strategy, but Player II wins. Let
$\mathcal {F}$
is a selective filter, the above is not a winning strategy for Player I and so, there is a match where Player I follows the strategy, but Player II wins. Let
![]() $\{a_n\}_{n\in \omega }$
,
$\{a_n\}_{n\in \omega }$
,
![]() $\{q_{\sigma }\}_{\sigma \in 2^{\omega }}$
,
$\{q_{\sigma }\}_{\sigma \in 2^{\omega }}$
,
![]() $\{s_{\sigma }\}_{\sigma \in 2^{\omega }}$
, and
$\{s_{\sigma }\}_{\sigma \in 2^{\omega }}$
, and
![]() $\{T_{\sigma }\}_{\sigma \in 2^{\omega }}$
be the sequences associated with one of these matches. To finish Case 1, define
$\{T_{\sigma }\}_{\sigma \in 2^{\omega }}$
be the sequences associated with one of these matches. To finish Case 1, define
![]() $q=\{\tau \in p\;|\;\exists \sigma \in 2^{\omega }\big (\tau \subseteq s_{\sigma }\big )\}$
. Moreover, if
$q=\{\tau \in p\;|\;\exists \sigma \in 2^{\omega }\big (\tau \subseteq s_{\sigma }\big )\}$
. Moreover, if
![]() $c_0$
is the constant
$c_0$
is the constant
![]() $0$
function in
$0$
function in
![]() $2^{\omega }$
and
$2^{\omega }$
and
![]() $\sigma \in 2^{<\omega }$
then
$\sigma \in 2^{<\omega }$
then
![]() $g_{\sigma }=\bigcup \{s_{\tau }\;|\; \tau \subseteq \sigma ^{\smallfrown } c_0\}\in T_{\sigma }$
and the set
$g_{\sigma }=\bigcup \{s_{\tau }\;|\; \tau \subseteq \sigma ^{\smallfrown } c_0\}\in T_{\sigma }$
and the set
![]() $Q=\{ g_{\sigma }\;|\;\sigma \in 2^{<\omega }\}$
is dense in
$Q=\{ g_{\sigma }\;|\;\sigma \in 2^{<\omega }\}$
is dense in
![]() $[q]$
. But then, by Lemma 2.4,
$[q]$
. But then, by Lemma 2.4,
![]() $q\in \mathbb {Q}(\mathcal {C})$
. Since for every
$q\in \mathbb {Q}(\mathcal {C})$
. Since for every
![]() $n\in \omega $
, every
$n\in \omega $
, every
![]() $\sigma \in 2^{n+1}$
, and every
$\sigma \in 2^{n+1}$
, and every
![]() $g\in [p(s_{\sigma })]$
, we have that
$g\in [p(s_{\sigma })]$
, we have that
![]() $a_n\in H(g)$
and every
$a_n\in H(g)$
and every
![]() $g\in [q]$
satisfies this condition for some
$g\in [q]$
satisfies this condition for some
![]() $\sigma \in 2^{n+1}$
, we obtain that for every
$\sigma \in 2^{n+1}$
, we obtain that for every
![]() $g\in [q]$
,
$g\in [q]$
,
![]() $\{a_n\}_{n\in \omega }\subseteq H(g)$
. In particular we have that
$\{a_n\}_{n\in \omega }\subseteq H(g)$
. In particular we have that
![]() $q\Vdash \{a_n\}_{n\in \omega }\subseteq \dot {X}$
. Since
$q\Vdash \{a_n\}_{n\in \omega }\subseteq \dot {X}$
. Since
![]() $\{a_n\}_{n\in \omega }\in \mathcal {F}$
, we are done.
$\{a_n\}_{n\in \omega }\in \mathcal {F}$
, we are done.
Case 2. There is
![]() $s_0\in p$
for which there is no
$s_0\in p$
for which there is no
![]() $s_0$
-special pair
$s_0$
-special pair
![]() $(q,T)$
. That is, every ordered pair
$(q,T)$
. That is, every ordered pair
![]() $(q,T)$
does not satisfy one of the following conditions:
$(q,T)$
does not satisfy one of the following conditions:
![]() $q\in \mathbb {S}$
is special,
$q\in \mathbb {S}$
is special,
![]() $T\in \mathcal {C}$
, or
$T\in \mathcal {C}$
, or
![]() $[q]\subseteq [p(s_0)]\cap T$
.
$[q]\subseteq [p(s_0)]\cap T$
.
In this case, we use Lemma 4.7 to find
![]() $q\in \mathbb {S}$
and
$q\in \mathbb {S}$
and
![]() $Y\in \mathcal {F}$
such that
$Y\in \mathcal {F}$
such that
![]() $q\subseteq p(s_0)$
and for every
$q\subseteq p(s_0)$
and for every
![]() $f\in [q]$
,
$f\in [q]$
,
![]() $Y\subseteq H(f)$
. Notice that q is special. Suppose towards a contradiction that
$Y\subseteq H(f)$
. Notice that q is special. Suppose towards a contradiction that
![]() $q\notin \mathbb {Q}(\mathcal {C})$
. Since every element of
$q\notin \mathbb {Q}(\mathcal {C})$
. Since every element of
![]() $\mathcal {C}$
is closed, this means that there is some
$\mathcal {C}$
is closed, this means that there is some
![]() $T\in \mathcal {C}$
such that
$T\in \mathcal {C}$
such that
![]() $T\cap [q]$
has non-empty interior in
$T\cap [q]$
has non-empty interior in
![]() $[q]$
and so we can find
$[q]$
and so we can find
![]() $\tau \in q$
such that
$\tau \in q$
such that
![]() $[q(\tau )]\subseteq T$
. Then
$[q(\tau )]\subseteq T$
. Then
![]() $(q(\tau ),T)$
is
$(q(\tau ),T)$
is
![]() $s_0$
-special, which is a contradiction. Therefore
$s_0$
-special, which is a contradiction. Therefore
![]() $q\in \mathbb {Q}(\mathcal {C})$
. To finish this case, just note that as before
$q\in \mathbb {Q}(\mathcal {C})$
. To finish this case, just note that as before
![]() $q\Vdash Y \subseteq \dot {X}$
.
$q\Vdash Y \subseteq \dot {X}$
.
Suppose that
![]() $\mathcal {C}$
is the partition of
$\mathcal {C}$
is the partition of
![]() $2^{\omega }$
in singletons. Then
$2^{\omega }$
in singletons. Then
![]() $\mathbb {Q}(\mathcal {C})=\mathbb {S}$
and so Case 1
of Theorem 4.8 never occurs. Therefore Lemma 4.7 actually yields a complete proof of Theorem 4.8 for Sacks forcing. Additionally, we obtain once again:
$\mathbb {Q}(\mathcal {C})=\mathbb {S}$
and so Case 1
of Theorem 4.8 never occurs. Therefore Lemma 4.7 actually yields a complete proof of Theorem 4.8 for Sacks forcing. Additionally, we obtain once again:
Corollary 4.9. The poset
![]() $\mathbb {Q}(\mathcal {C})$
preserves selective ultrafilters.
$\mathbb {Q}(\mathcal {C})$
preserves selective ultrafilters.
Corollary 4.10. Let
![]() $\mathcal {A}$
be a selective independent family and let G be a
$\mathcal {A}$
be a selective independent family and let G be a
![]() $\mathbb Q(\mathcal {C})$
-generic filter. Then, in
$\mathbb Q(\mathcal {C})$
-generic filter. Then, in
![]() $V[G]$
,
$V[G]$
,
![]() $\mathcal {A}$
is still selective independent.
$\mathcal {A}$
is still selective independent.
Proof Since
![]() $\mathbb {Q}(\mathcal {C})$
is proper and has the Sacks property,
$\mathbb {Q}(\mathcal {C})$
is proper and has the Sacks property,
![]() $\langle \operatorname {\mathrm {fil}}(\mathcal {A})^V \rangle $
is a selective filter in
$\langle \operatorname {\mathrm {fil}}(\mathcal {A})^V \rangle $
is a selective filter in
![]() $V[G]$
, but by Lemma 3.4 we know that
$V[G]$
, but by Lemma 3.4 we know that
![]() $\operatorname {\mathrm {fil}}(\mathcal {A})^{V[G]}=\langle \operatorname {\mathrm {fil}}(\mathcal {A})^V \rangle $
. To show that
$\operatorname {\mathrm {fil}}(\mathcal {A})^{V[G]}=\langle \operatorname {\mathrm {fil}}(\mathcal {A})^V \rangle $
. To show that
![]() $\mathcal {A}$
remains densely maximal in
$\mathcal {A}$
remains densely maximal in
![]() $V[G]$
, note that by Theorem 4.8, the family
$V[G]$
, note that by Theorem 4.8, the family
![]() $P(\omega )^V\backslash \operatorname {\mathrm {fil}}(\mathcal {A})^V$
is cofinal in
$P(\omega )^V\backslash \operatorname {\mathrm {fil}}(\mathcal {A})^V$
is cofinal in
![]() $P(\omega )^{V[G]}\backslash \langle \operatorname {\mathrm {fil}}(\mathcal {A})^V\rangle $
. However, by hypothesis
$P(\omega )^{V[G]}\backslash \langle \operatorname {\mathrm {fil}}(\mathcal {A})^V\rangle $
. However, by hypothesis
![]() $\{\omega \backslash \mathcal {A}^h:h\in \operatorname {\mathrm {FF}}(\mathcal {A})\}$
is cofinal in
$\{\omega \backslash \mathcal {A}^h:h\in \operatorname {\mathrm {FF}}(\mathcal {A})\}$
is cofinal in
![]() $P(\omega )^V\backslash \operatorname {\mathrm {fil}}(\mathcal {A})^V$
and so we are done.
$P(\omega )^V\backslash \operatorname {\mathrm {fil}}(\mathcal {A})^V$
and so we are done.
5 No small ultrafilter bases and tightness
5.1 The poset
 $\mathbb {Q}_{\mathcal {I}}$
$\mathbb {Q}_{\mathcal {I}}$
For a maximal ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
,
$\omega $
,
![]() $\mathbb {Q}_{\mathcal {I}}$
denotes the forcing notion introduced by Shelah in [Reference Shelah46] for obtaining the consistency of
$\mathbb {Q}_{\mathcal {I}}$
denotes the forcing notion introduced by Shelah in [Reference Shelah46] for obtaining the consistency of
![]() $\mathfrak {i}<\mathfrak {u}$
. In [Reference Shelah46] it is shown that
$\mathfrak {i}<\mathfrak {u}$
. In [Reference Shelah46] it is shown that
![]() $\mathbb {Q}_{\mathcal {I}}$
is proper [Reference Shelah46, Claim 1.13],
$\mathbb {Q}_{\mathcal {I}}$
is proper [Reference Shelah46, Claim 1.13],
![]() ${}^{\omega }\omega $
-bounding [Reference Shelah46, Claim 1.12], and even has the Sacks property [Reference Shelah46, Claim 1.12]. In the
${}^{\omega }\omega $
-bounding [Reference Shelah46, Claim 1.12], and even has the Sacks property [Reference Shelah46, Claim 1.12]. In the
![]() $\mathbb {Q}_{\mathcal {I}}$
-generic extension,
$\mathbb {Q}_{\mathcal {I}}$
-generic extension,
![]() $\mathcal {I}$
is no longer a maximal ideal [Reference Shelah46, Claim 1.5]. For completeness of the presentation we repeat below the definition and some of the key properties of
$\mathcal {I}$
is no longer a maximal ideal [Reference Shelah46, Claim 1.5]. For completeness of the presentation we repeat below the definition and some of the key properties of
![]() $\mathbb {Q}_{\mathcal {I}}$
.
$\mathbb {Q}_{\mathcal {I}}$
.
Definition 5.1. Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega $
.
$\omega $
.
-
(1) An equivalence relation E on a subset of
 $\omega $
is an
$\omega $
is an
 $\mathcal {I}$
-equivalence relation if
$\mathcal {I}$
-equivalence relation if
 $\operatorname {\mathrm {dom}} E\in \mathcal {I}^{\ast }$
and each E-equivalence class is in
$\operatorname {\mathrm {dom}} E\in \mathcal {I}^{\ast }$
and each E-equivalence class is in
 $\mathcal {I}$
.
$\mathcal {I}$
. -
(2) For
 $\mathcal {I}$
-equivalence relations
$\mathcal {I}$
-equivalence relations
 $E_1,E_2$
, we denote
$E_1,E_2$
, we denote
 $E_1\leq _{\mathcal {I}} E_2$
if
$E_1\leq _{\mathcal {I}} E_2$
if
 $\operatorname {\mathrm {dom}} E_1\subseteq \operatorname {\mathrm {dom}} E_2$
, and
$\operatorname {\mathrm {dom}} E_1\subseteq \operatorname {\mathrm {dom}} E_2$
, and
 $E_1$
-equivalence classes are unions of
$E_1$
-equivalence classes are unions of
 $E_2$
-equivalence classes.
$E_2$
-equivalence classes. -
(3) Let
 $A\subseteq \omega $
. A function g is A-n-determined if
$A\subseteq \omega $
. A function g is A-n-determined if
 $g\colon {}^A\{0,1\}\to \{0,1\}$
and there is
$g\colon {}^A\{0,1\}\to \{0,1\}$
and there is
 $w\subseteq A\cap (n+1)$
such that for any
$w\subseteq A\cap (n+1)$
such that for any
 $\eta ,\nu \in {}^A\{0,1\}$
with
$\eta ,\nu \in {}^A\{0,1\}$
with
 $\eta \restriction w=\nu \restriction w$
we have
$\eta \restriction w=\nu \restriction w$
we have
 $g(\eta )=g(\nu )$
.
$g(\eta )=g(\nu )$
.
For
![]() $i\in A$
, by
$i\in A$
, by
![]() $g_i$
we denote the function from
$g_i$
we denote the function from
![]() ${}^A\{0,1\}$
to
${}^A\{0,1\}$
to
![]() $\{0,1\}$
which maps
$\{0,1\}$
which maps
![]() $\eta \in {}^A\{0,1\}$
to
$\eta \in {}^A\{0,1\}$
to
![]() $\eta (i)$
.
$\eta (i)$
.
Claim 5.2. Each A-n-determined function is equal to a function
![]() $\varphi (g_0,\dots ,g_n)$
which is obtained as an interpretation of a formula
$\varphi (g_0,\dots ,g_n)$
which is obtained as an interpretation of a formula
![]() $\varphi (a_0,\dots ,a_n)$
of propositional calculus. The symbols
$\varphi (a_0,\dots ,a_n)$
of propositional calculus. The symbols
![]() $\wedge $
,
$\wedge $
,
![]() $\vee $
,
$\vee $
,
![]() $\neg $
are interpreted as a maximum, minimum, and complement (i.e.,
$\neg $
are interpreted as a maximum, minimum, and complement (i.e.,
![]() $1-g_i$
), respectively. The formula
$1-g_i$
), respectively. The formula
![]() $\varphi (a_0,\dots ,a_n)$
may contain constant symbols
$\varphi (a_0,\dots ,a_n)$
may contain constant symbols
![]() $0,1$
which are interpreted as constant functions
$0,1$
which are interpreted as constant functions
![]() $0,1$
.
$0,1$
.
For an
![]() $\mathcal {I}$
-equivalence relation E we denote
$\mathcal {I}$
-equivalence relation E we denote
![]() $A=A(E)=\{x\colon x\in \operatorname {\mathrm {dom}} E, x=\min [x]_E\}$
.
$A=A(E)=\{x\colon x\in \operatorname {\mathrm {dom}} E, x=\min [x]_E\}$
.
Definition 5.3 (Set of conditions in
 $\mathbb {Q}_{\mathcal {I}}$
).
$\mathbb {Q}_{\mathcal {I}}$
).
Let
![]() $\mathcal {I}$
be an ideal on
$\mathcal {I}$
be an ideal on
![]() $\omega $
. We define a forcing notion
$\omega $
. We define a forcing notion
![]() $\mathbb {Q}_{\mathcal {I}}$
:
$\mathbb {Q}_{\mathcal {I}}$
:
-
(1) E is an
 $\mathcal {I}$
-equivalence relation,
$\mathcal {I}$
-equivalence relation, -
(2) H is a function with
 $\operatorname {\mathrm {dom}} H=\omega $
,
$\operatorname {\mathrm {dom}} H=\omega $
, -
(3) a value
 $H(n)$
is an
$H(n)$
is an
 $A(E)$
-n-determined function,
$A(E)$
-n-determined function, -
(4) if
 $n\in A(E)$
then
$n\in A(E)$
then
 $H(n)=g_n$
,
$H(n)=g_n$
, -
(5) if
 $n\in \operatorname {\mathrm {dom}} E\setminus A(E)$
and
$n\in \operatorname {\mathrm {dom}} E\setminus A(E)$
and
 $nEi$
for
$nEi$
for
 $i\in A(E)$
then
$i\in A(E)$
then
 $H(n)$
is
$H(n)$
is
 $g_i$
or
$g_i$
or
 $1-g_i$
.
$1-g_i$
.
For a condition
![]() $q\in \mathbb {Q}_{\mathcal {I}}$
, let
$q\in \mathbb {Q}_{\mathcal {I}}$
, let
![]() $A^q$
be
$A^q$
be
![]() $A(E^q)$
in the following.
$A(E^q)$
in the following.
Definition 5.4. If
![]() $p,q\in \mathbb {Q}_{\mathcal {I}}$
with
$p,q\in \mathbb {Q}_{\mathcal {I}}$
with
![]() $A^p\subseteq A^q$
then for each
$A^p\subseteq A^q$
then for each
![]() $n\in \omega \backslash \operatorname {\mathrm {dom}}(E^q)$
we write
$n\in \omega \backslash \operatorname {\mathrm {dom}}(E^q)$
we write
![]() $H^p(n)=^{\ast \ast }H^q(n)$
if for each
$H^p(n)=^{\ast \ast }H^q(n)$
if for each
![]() $\eta \in {}^{A^p}\{0,1\}$
we have
$\eta \in {}^{A^p}\{0,1\}$
we have
![]() $H^p(n)(\eta )=H^q(n)(\eta ')$
where
$H^p(n)(\eta )=H^q(n)(\eta ')$
where
 $$\begin{align*}\eta'(j)= \begin{cases} \eta(j),&j\in A^p,\\ H^p(j)(\eta),&j\in A^q\setminus A^p. \end{cases} \end{align*}$$
$$\begin{align*}\eta'(j)= \begin{cases} \eta(j),&j\in A^p,\\ H^p(j)(\eta),&j\in A^q\setminus A^p. \end{cases} \end{align*}$$
Definition 5.5 (The order of
 $\mathbb {Q}_{\mathcal {I}}$
).
$\mathbb {Q}_{\mathcal {I}}$
).
If
![]() $p,q\in \mathbb {Q}_{\mathcal {I}}$
then
$p,q\in \mathbb {Q}_{\mathcal {I}}$
then
![]() $p\leq q$
if:
$p\leq q$
if:
-
(1)
 $E^p\leq _{\mathcal {I}} E^q$
.
$E^p\leq _{\mathcal {I}} E^q$
. -
(2) If
 $H^q(n)=g_i$
for
$H^q(n)=g_i$
for
 $n\in \operatorname {\mathrm {dom}} E^q$
then
$n\in \operatorname {\mathrm {dom}} E^q$
then
 $H^p(n)=H^p(i)$
.
$H^p(n)=H^p(i)$
. -
(3) If
 $H^q(n)=1-g_i$
for
$H^q(n)=1-g_i$
for
 $n\in \operatorname {\mathrm {dom}} E^q$
then
$n\in \operatorname {\mathrm {dom}} E^q$
then
 $H^p(n)=1-H^p(i)$
.
$H^p(n)=1-H^p(i)$
. -
(4) If
 $n\in \omega \setminus \operatorname {\mathrm {dom}} E^q$
then
$n\in \omega \setminus \operatorname {\mathrm {dom}} E^q$
then
 $H^p(n)=^{\ast \ast }H^q(n)$
.
$H^p(n)=^{\ast \ast }H^q(n)$
.
Finally,
![]() $p\leq _nq$
if
$p\leq _nq$
if
![]() $p\leq q$
and
$p\leq q$
and
![]() $A^p$
contains the first n elements of
$A^p$
contains the first n elements of
![]() $A^q$
.
$A^q$
.
The following has been proven in [Reference Shelah46]. Items (1) and (2) correspond to [Reference Shelah46, Claim 1.7(2)], and item (3) is a straightforward modification of [Reference Shelah46, Claim 1.8].
Claim 5.6. Let
![]() $p\in \mathbb {Q}_{\mathcal {I}}$
. For an initial segment u of
$p\in \mathbb {Q}_{\mathcal {I}}$
. For an initial segment u of
![]() $A^p$
, and
$A^p$
, and
![]() $h\colon u\to \{0,1\}$
, let
$h\colon u\to \{0,1\}$
, let
![]() $p^{[h]}$
be the pair
$p^{[h]}$
be the pair
![]() $q=(H^q,E^q)$
defined by (i) and (ii) below:
$q=(H^q,E^q)$
defined by (i) and (ii) below:
-
(i)
 $E^q=E^p\restriction \bigcup \{[i]_{E^p}\colon i\in A^p\setminus u\}$
.
$E^q=E^p\restriction \bigcup \{[i]_{E^p}\colon i\in A^p\setminus u\}$
. -
(ii) If
 $H^p(n)$
is
$H^p(n)$
is
 $\varphi (g_0,\dots ,g_n)$
then
$\varphi (g_0,\dots ,g_n)$
then
 $H^q(n)$
is
$H^q(n)$
is
 $\varphi (g_0,\dots ,g_i/h(i),\dots ,g_n)$
, where the substitution is done just for
$\varphi (g_0,\dots ,g_i/h(i),\dots ,g_n)$
, where the substitution is done just for
 $i\in u$
.
$i\in u$
.
Then we have:
-
(1)
 $p^{[h]}$
is a condition in
$p^{[h]}$
is a condition in
 $\mathbb {Q}_{\mathcal {I}}$
stronger than p.
$\mathbb {Q}_{\mathcal {I}}$
stronger than p. -
(2) The set
 $\{p^{[h]}\colon h\in {}^u\{0,1\}\}$
is predense below p.
$\{p^{[h]}\colon h\in {}^u\{0,1\}\}$
is predense below p. -
(3) If u is the set of first n elements of
 $A^p$
, D a dense subset of
$A^p$
, D a dense subset of
 $\mathbb {Q}_{\mathcal {I}}$
then there is
$\mathbb {Q}_{\mathcal {I}}$
then there is
 $q\in \mathbb {Q}_{\mathcal {I}}$
such that
$q\in \mathbb {Q}_{\mathcal {I}}$
such that
 $q\leq _np$
and
$q\leq _np$
and
 $q^{[h]}\in D$
for any
$q^{[h]}\in D$
for any
 $h\in {}^u\{0,1\}$
.
$h\in {}^u\{0,1\}$
.
Definition 5.7 (The game GM
 $_{\mathcal {I}}(E)$
).
$_{\mathcal {I}}(E)$
).
GM
![]() $_{\mathcal {I}}(E)$
is the following game. In the n-th move, the first player chooses an
$_{\mathcal {I}}(E)$
is the following game. In the n-th move, the first player chooses an
![]() $\mathcal {I}$
-equivalence relation
$\mathcal {I}$
-equivalence relation
![]() $E^1_n\leq _{\mathcal {I}} E^2_{n-1}$
(
$E^1_n\leq _{\mathcal {I}} E^2_{n-1}$
(
![]() $E^1_0=E$
), and the second player chooses an
$E^1_0=E$
), and the second player chooses an
![]() $\mathcal {I}$
-equivalence relation
$\mathcal {I}$
-equivalence relation
![]() $E^2_n\leq _{\mathcal {I}} E^1_n$
. In the end, the second player wins if
$E^2_n\leq _{\mathcal {I}} E^1_n$
. In the end, the second player wins if
Otherwise, the first player wins.
Remark 5.8. If the second player wins in the game GM
![]() $_{\mathcal {I}}(E)$
, then the game is invariant to taking subsets. That is, the game is invariant to taking
$_{\mathcal {I}}(E)$
, then the game is invariant to taking subsets. That is, the game is invariant to taking
![]() $\leq _{\mathcal {I}}$
-extensions
$\leq _{\mathcal {I}}$
-extensions
![]() $\{E^{2,*}_n\}_{n\in \omega }$
with
$\{E^{2,*}_n\}_{n\in \omega }$
with
![]() $\operatorname {\mathrm {dom}}(E^{2,*}_n)\subseteq \operatorname {\mathrm {dom}} E^2_n$
.
$\operatorname {\mathrm {dom}}(E^{2,*}_n)\subseteq \operatorname {\mathrm {dom}} E^2_n$
.
The next lemma corresponds to [Reference Shelah46, Claim 1.10(1)]
Lemma 5.9. The game GM
![]() $_{\mathcal {I}}(E)$
is not determined for a maximal ideal
$_{\mathcal {I}}(E)$
is not determined for a maximal ideal
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
5.2 Tight MAD families
Tight MAD families were investigated in [Reference Guzmán, Hrušák and Téllez25, Reference Kurilič33, Reference Malykhin36]. An AD family
![]() $\mathcal {A}$
is called tight if for every
$\mathcal {A}$
is called tight if for every
![]() $\{X_n\colon n\in \omega \}\subseteq \mathcal {I}(\mathcal {A})^+$
there is
$\{X_n\colon n\in \omega \}\subseteq \mathcal {I}(\mathcal {A})^+$
there is
![]() $B\in \mathcal {I}(\mathcal {A})$
such that
$B\in \mathcal {I}(\mathcal {A})$
such that
![]() $B\cap X_n$
is infinite for every
$B\cap X_n$
is infinite for every
![]() $n\in \omega $
.
$n\in \omega $
.
A preservation theorem for tight MAD family under countable support iteration of proper forcing notions was developed by Guzmán, Hrušák, and Téllez [Reference Guzmán, Hrušák and Téllez25].
Definition 5.10. Let
![]() $\mathcal {A}$
be a tight MAD family. A proper forcing
$\mathcal {A}$
be a tight MAD family. A proper forcing
![]() $\mathbb {P}$
strongly preserves the tightness of
$\mathbb {P}$
strongly preserves the tightness of
![]() $\mathcal {A}$
if for every
$\mathcal {A}$
if for every
![]() $p\in \mathbb {P}$
, M a countable elementary submodel of
$p\in \mathbb {P}$
, M a countable elementary submodel of
![]() $H(\kappa )$
(where
$H(\kappa )$
(where
![]() $\kappa $
is a large enough regular cardinal) such that
$\kappa $
is a large enough regular cardinal) such that
![]() $\mathbb {P}, \mathcal {A}, p\in M$
and
$\mathbb {P}, \mathcal {A}, p\in M$
and
![]() $B\in \mathcal {I}(\mathcal {A})$
for which
$B\in \mathcal {I}(\mathcal {A})$
for which
![]() $|B\cap Y|=\omega $
for every
$|B\cap Y|=\omega $
for every
![]() $Y\in \mathcal {I}(\mathcal {A})^+\cap M$
, there is
$Y\in \mathcal {I}(\mathcal {A})^+\cap M$
, there is
![]() $q\leq p$
an (
$q\leq p$
an (
![]() $M,\mathbb {P}$
)-generic condition such that
$M,\mathbb {P}$
)-generic condition such that
where
![]() $\dot {G}$
denotes the name of the generic filter.
$\dot {G}$
denotes the name of the generic filter.
We restate Corollary 32 of [Reference Guzmán, Hrušák and Téllez25] which is crucial for preserving MAD families in the forthcoming model.
Theorem 5.11 (Guzmán, Hrušák, and Téllez).
Let
![]() $\mathcal {A}$
be a tight MAD family. If the sequence
$\mathcal {A}$
be a tight MAD family. If the sequence
![]() $\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta }\colon \alpha \leq \omega _2,\beta <\omega _2\rangle $
is a countable support iteration of proper posets such that
$\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta }\colon \alpha \leq \omega _2,\beta <\omega _2\rangle $
is a countable support iteration of proper posets such that
then
![]() $\mathbb {P}_{\omega _2}\Vdash _{\alpha }\text {"}\mathcal {A}\text { is a~tight }\mathrm {\texttt {MAD}}\ \text {family}.\text {"}$
$\mathbb {P}_{\omega _2}\Vdash _{\alpha }\text {"}\mathcal {A}\text { is a~tight }\mathrm {\texttt {MAD}}\ \text {family}.\text {"}$
We need the following fact about the outer hulls observed in [Reference Guzmán, Hrušák and Téllez25].
Lemma 5.12. Let
![]() $\mathcal {A}$
be an AD family,
$\mathcal {A}$
be an AD family,
![]() $\mathbb {P}$
a partial order,
$\mathbb {P}$
a partial order,
![]() $\dot {B}$
a
$\dot {B}$
a
![]() $\mathbb {P}$
-name for a subset of
$\mathbb {P}$
-name for a subset of
![]() $\omega $
, and
$\omega $
, and
![]() $p\in \mathbb {P}$
such that
$p\in \mathbb {P}$
such that
![]() $p\Vdash \text {"}\dot {B}\in \mathcal {I}(\mathcal {A})^+.\text {"}$
Then the set
$p\Vdash \text {"}\dot {B}\in \mathcal {I}(\mathcal {A})^+.\text {"}$
Then the set
![]() $\{n\colon (\exists q\leq p)\ q\Vdash \text {"}n\in \dot {B}\text {"}\}$
is in
$\{n\colon (\exists q\leq p)\ q\Vdash \text {"}n\in \dot {B}\text {"}\}$
is in
![]() $\mathcal {I}(\mathcal {A})^+$
.
$\mathcal {I}(\mathcal {A})^+$
.
And now we are ready to show the main result of this section.
Theorem 5.13. Let
![]() $\mathcal {A}$
be a tight MAD family,
$\mathcal {A}$
be a tight MAD family,
![]() $\mathcal {I}$
being a maximal proper ideal on
$\mathcal {I}$
being a maximal proper ideal on
![]() $\omega $
. The poset
$\omega $
. The poset
![]() $\mathbb {Q}_{\mathcal {I}}$
strongly preserves the tightness of
$\mathbb {Q}_{\mathcal {I}}$
strongly preserves the tightness of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof Let
![]() $p\in \mathbb {Q}_{\mathcal {I}}$
, M a countable elementary submodel of
$p\in \mathbb {Q}_{\mathcal {I}}$
, M a countable elementary submodel of
![]() $H(\kappa )$
such that
$H(\kappa )$
such that
![]() $\mathcal {I}, \mathcal {A}, p\in M$
and
$\mathcal {I}, \mathcal {A}, p\in M$
and
![]() $B\in \mathcal {I}(\mathcal {A})$
for which
$B\in \mathcal {I}(\mathcal {A})$
for which
![]() $|B\cap Y|=\omega $
for every
$|B\cap Y|=\omega $
for every
![]() $Y\in \mathcal {I}(\mathcal {A})^+\cap M$
. We fix an enumeration
$Y\in \mathcal {I}(\mathcal {A})^+\cap M$
. We fix an enumeration
![]() $\{D_n\colon n\in \omega \}$
of all open dense subsets of
$\{D_n\colon n\in \omega \}$
of all open dense subsets of
![]() $\mathbb {Q}_{\mathcal {I}}$
that are in M, and an enumeration
$\mathbb {Q}_{\mathcal {I}}$
that are in M, and an enumeration
![]() $\{\dot {Z}_n\colon n\in \omega \}$
with infinite repetitions of all
$\{\dot {Z}_n\colon n\in \omega \}$
with infinite repetitions of all
![]() $\mathbb {Q}_{\mathcal {I}}$
-names for elements of
$\mathbb {Q}_{\mathcal {I}}$
-names for elements of
![]() $\mathcal {I}(\mathcal {A})^+$
that are in M.
$\mathcal {I}(\mathcal {A})^+$
that are in M.
We define a strategy for the first player in the game GM
![]() $_{\mathcal {I}}(E)$
, which cannot be winning in all rounds. Work in M. We set
$_{\mathcal {I}}(E)$
, which cannot be winning in all rounds. Work in M. We set
![]() $p_0=q_0=p$
and
$p_0=q_0=p$
and
![]() $u_0=\emptyset $
. We assume that the first player has chosen
$u_0=\emptyset $
. We assume that the first player has chosen
![]() $E^1_n$
,
$E^1_n$
,
![]() $q_n$
,
$q_n$
,
![]() $p_n$
,
$p_n$
,
![]() $u_n$
, and the second one has chosen
$u_n$
, and the second one has chosen
![]() $E^2_n$
. We give instructions to choose
$E^2_n$
. We give instructions to choose
![]() $E^1_{n+1}$
,
$E^1_{n+1}$
,
![]() $q_{n+1}$
,
$q_{n+1}$
,
![]() $p_{n+1}$
,
$p_{n+1}$
,
![]() $u_{n+1}$
. We begin with
$u_{n+1}$
. We begin with
![]() $q_{n+1}$
:
$q_{n+1}$
:
-
(1)
 $\operatorname {\mathrm {dom}} E^{q_{n+1}}=\operatorname {\mathrm {dom}} E^{p_n}$
.
$\operatorname {\mathrm {dom}} E^{q_{n+1}}=\operatorname {\mathrm {dom}} E^{p_n}$
. -
(2)
 $xE^{q_{n+1}}y$
iff one of the following holds:
$xE^{q_{n+1}}y$
iff one of the following holds:-
(i)
 $xE^2_ny$
.
$xE^2_ny$
. -
(ii) There is
 $k\in u_n$
with
$k\in u_n$
with
 $x,y\in [k]_{E^{p_n}}$
and
$x,y\in [k]_{E^{p_n}}$
and
 $x,y\not \in \operatorname {\mathrm {dom}} E^2_n$
.
$x,y\not \in \operatorname {\mathrm {dom}} E^2_n$
. -
(iii)
 $x,y\notin \bigcup \{[i]_{E^{p_n}}:i\in u_n\}\cup \operatorname {\mathrm {dom}} E^2_n$
.
$x,y\notin \bigcup \{[i]_{E^{p_n}}:i\in u_n\}\cup \operatorname {\mathrm {dom}} E^2_n$
.
-
-
(3)
 $H^{q_{n+1}}$
is chosen such that:
$H^{q_{n+1}}$
is chosen such that:-
(i) If
 $l\in A^{q_{n+1}}$
, then
$l\in A^{q_{n+1}}$
, then
 $H^{q_{n+1}}(l)=g_l$
.
$H^{q_{n+1}}(l)=g_l$
. -
(ii) If
 $l\in A^{p_n}\backslash A^{q_{n+1}}$
, then
$l\in A^{p_n}\backslash A^{q_{n+1}}$
, then
 $H^{q_{n+1}}(l)=g_{\min [l]_{E^{q_{n+1}}}}$
.
$H^{q_{n+1}}(l)=g_{\min [l]_{E^{q_{n+1}}}}$
. -
(iii) If
 $l\in \operatorname {\mathrm {dom}} E^{p_n}\setminus A^{p_n}$
,
$l\in \operatorname {\mathrm {dom}} E^{p_n}\setminus A^{p_n}$
,
 $H^{p_n}(l)=g_i$
then
$H^{p_n}(l)=g_i$
then
 $H^{q_{n+1}}(l)=H^{q_{n+1}}(i)$
.
$H^{q_{n+1}}(l)=H^{q_{n+1}}(i)$
. -
(iv) If
 $l\in \operatorname {\mathrm {dom}} E^{p_n}\setminus A^{p_n}$
,
$l\in \operatorname {\mathrm {dom}} E^{p_n}\setminus A^{p_n}$
,
 $H^{p_n}(l)=1-g_i$
then
$H^{p_n}(l)=1-g_i$
then
 $H^{q_{n+1}}(l)=1-H^{q_{n+1}}(i)$
.
$H^{q_{n+1}}(l)=1-H^{q_{n+1}}(i)$
. -
(v) If
 $l\in \omega \setminus \operatorname {\mathrm {dom}} E^{p_n}$
then
$l\in \omega \setminus \operatorname {\mathrm {dom}} E^{p_n}$
then
 $H^{q_{n+1}}(l)=^{\ast \ast }H^{p_n}(l)$
.
$H^{q_{n+1}}(l)=^{\ast \ast }H^{p_n}(l)$
.
-
Note that for the already defined condition
![]() $q_{n+1}$
we have
$q_{n+1}$
we have
![]() $q_{n+1}\leq _n p_n$
. Let
$q_{n+1}\leq _n p_n$
. Let
![]() $z^n$
be the least element of
$z^n$
be the least element of
![]() $\operatorname {\mathrm {dom}} E^{q_{n+1}}$
generating the
$\operatorname {\mathrm {dom}} E^{q_{n+1}}$
generating the
![]() $E^{q_{n+1}}$
-equivalence class of (2)(iii) above and let
$E^{q_{n+1}}$
-equivalence class of (2)(iii) above and let
![]() $u_{n+1}=u_n\cup \{z^n\}$
. By Lemma 5.12, the set
$u_{n+1}=u_n\cup \{z^n\}$
. By Lemma 5.12, the set
![]() $D^{\prime }_n=\{r\in \mathbb {Q}_{\mathcal {I}}\colon r\Vdash \text {"}(\dot {Z}_n\cap B)\setminus n\neq \emptyset \text {"}\}$
is open dense below p (and also below
$D^{\prime }_n=\{r\in \mathbb {Q}_{\mathcal {I}}\colon r\Vdash \text {"}(\dot {Z}_n\cap B)\setminus n\neq \emptyset \text {"}\}$
is open dense below p (and also below
![]() $q_{n+1}$
). Then
$q_{n+1}$
). Then
![]() $D^{\prime }_n\cap D_n$
is dense below
$D^{\prime }_n\cap D_n$
is dense below
![]() $q_{n+1}$
. Therefore we can apply Claim 5.6(3) to obtain
$q_{n+1}$
. Therefore we can apply Claim 5.6(3) to obtain
![]() $p_{n+1}\leq _{n+1} q_{n+1}$
such that for each
$p_{n+1}\leq _{n+1} q_{n+1}$
such that for each
![]() $h\in {}^{u_{n+1}}\{0,1\}$
, the condition
$h\in {}^{u_{n+1}}\{0,1\}$
, the condition
![]() $p^{[h]}_{n+1} \in D^{\prime }_n\cap D_n\cap M$
. In particular, if
$p^{[h]}_{n+1} \in D^{\prime }_n\cap D_n\cap M$
. In particular, if
![]() $h\in {}^{u_{n+1}}\{0,1\}$
then
$h\in {}^{u_{n+1}}\{0,1\}$
then
![]() $p_{n+1}^{[h]}\Vdash \text {"} (\dot {Z}_n\cap B)\setminus n\neq \emptyset \text {"}$
and
$p_{n+1}^{[h]}\Vdash \text {"} (\dot {Z}_n\cap B)\setminus n\neq \emptyset \text {"}$
and
![]() $p_{n+1}^{[h]}\in D_n\cap M$
. By Claim 5.6(2) we have
$p_{n+1}^{[h]}\in D_n\cap M$
. By Claim 5.6(2) we have
![]() $p_{n+1}\Vdash \text {"} (\dot {Z}_n\cap B)\setminus n\neq \emptyset .\text {"}$
Finally, we set
$p_{n+1}\Vdash \text {"} (\dot {Z}_n\cap B)\setminus n\neq \emptyset .\text {"}$
Finally, we set
We define a fusion q of the sequence
![]() $\langle p_n\colon n\in \omega \rangle $
. The relation
$\langle p_n\colon n\in \omega \rangle $
. The relation
![]() $E^q$
has
$E^q$
has
![]() $\operatorname {\mathrm {dom}} E^q=\bigcap _{n\in \omega }\operatorname {\mathrm {dom}} E^{p_n}$
and
$\operatorname {\mathrm {dom}} E^q=\bigcap _{n\in \omega }\operatorname {\mathrm {dom}} E^{p_n}$
and
![]() $xE^qy$
if for every n large enough,
$xE^qy$
if for every n large enough,
![]() $xE^{p_n}y$
. The function
$xE^{p_n}y$
. The function
![]() $H^q$
is equal to
$H^q$
is equal to
![]() $H^{p_n}$
for large enough n. In order to guarantee that
$H^{p_n}$
for large enough n. In order to guarantee that
![]() $\operatorname {\mathrm {dom}} E^q\in \mathcal {I}^*$
, it is sufficient to choose a play with the first player using the described strategy, but loosing, which by Lemma 5.9 exists. The other properties for
$\operatorname {\mathrm {dom}} E^q\in \mathcal {I}^*$
, it is sufficient to choose a play with the first player using the described strategy, but loosing, which by Lemma 5.9 exists. The other properties for
![]() $q\in \mathbb {Q}_{\mathcal {I}}$
are satisfied by the definition of q.
$q\in \mathbb {Q}_{\mathcal {I}}$
are satisfied by the definition of q.
Finally q is (M,
![]() $\mathbb {Q}_{\mathcal {I}}$
)-generic,
$\mathbb {Q}_{\mathcal {I}}$
)-generic,
![]() $q\leq _n p_n$
for all n and so
$q\leq _n p_n$
for all n and so
![]() $q\Vdash \text {"}(\forall \dot {Z}\in \mathcal {I}(\mathcal {A})\cap M[\dot {G}])\ |\dot {Z}\cap B|=\omega .\text {"}$
$q\Vdash \text {"}(\forall \dot {Z}\in \mathcal {I}(\mathcal {A})\cap M[\dot {G}])\ |\dot {Z}\cap B|=\omega .\text {"}$
As a corollary we obtain that in Shelah’s model of
![]() $\mathfrak {i}<\mathfrak {u}$
(see [Reference Shelah46]), also the almost disjointness number is small.
$\mathfrak {i}<\mathfrak {u}$
(see [Reference Shelah46]), also the almost disjointness number is small.
Corollary 5.14. It is relatively consistent that
![]() $\mathfrak {a}=\mathfrak {i}<\mathfrak {u}$
.
$\mathfrak {a}=\mathfrak {i}<\mathfrak {u}$
.
Moreover, using the preservation results of the current article, together with the preservation results of [Reference Guzmán, Hrušák and Téllez25], as well as the fact that
![]() $\mathbb {Q}_{\mathcal {I}}$
has the Sacks property, we obtain:
$\mathbb {Q}_{\mathcal {I}}$
has the Sacks property, we obtain:
Corollary 5.15. It is relatively consistent that
![]() $\operatorname {\mathrm {cof}}(\mathcal {N})=\mathfrak {i}=\mathfrak {a}=\omega _1<\mathfrak {a}_T=\mathfrak {u}\,{=}\,\omega _2$
.
$\operatorname {\mathrm {cof}}(\mathcal {N})=\mathfrak {i}=\mathfrak {a}=\omega _1<\mathfrak {a}_T=\mathfrak {u}\,{=}\,\omega _2$
.
Proof Work over a model of
![]() $\textsf {CH}$
. Let
$\textsf {CH}$
. Let
![]() $\mathcal {A}_0$
be Shelah’s selective independent family and let
$\mathcal {A}_0$
be Shelah’s selective independent family and let
![]() $\mathcal {A}_1$
be a tight mad family. Using an appropriate bookkeeping device define a countable support iteration
$\mathcal {A}_1$
be a tight mad family. Using an appropriate bookkeeping device define a countable support iteration
![]() $\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta }\colon \alpha \leq \omega _2,\beta <\omega _2\rangle $
of posets such that for even
$\langle \mathbb {P}_{\alpha },\dot {\mathbb {Q}}_{\beta }\colon \alpha \leq \omega _2,\beta <\omega _2\rangle $
of posets such that for even
![]() $\alpha $
,
$\alpha $
,
![]() $\mathbb {P}_{\alpha }$
forces that
$\mathbb {P}_{\alpha }$
forces that
![]() $\mathbb {Q}_{\alpha }=\mathbb {Q}(\mathcal {C})$
for some uncountable partition
$\mathbb {Q}_{\alpha }=\mathbb {Q}(\mathcal {C})$
for some uncountable partition
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $2^{\omega }$
into compact sets, for odd
$2^{\omega }$
into compact sets, for odd
![]() $\alpha $
,
$\alpha $
,
![]() $\mathbb {P}_{\alpha }$
forces that
$\mathbb {P}_{\alpha }$
forces that
![]() $\mathbb {Q}_{\alpha }=\mathbb {Q}_{\mathcal {I}}$
for some maximal ideal
$\mathbb {Q}_{\alpha }=\mathbb {Q}_{\mathcal {I}}$
for some maximal ideal
![]() $\mathcal {I}$
on
$\mathcal {I}$
on
![]() $\omega $
, and such that
$\omega $
, and such that
![]() $V^{\mathbb {P}_{\omega _2}}\vDash \mathfrak {a}_T=\mathfrak {u}=\omega _2$
. The iteration
$V^{\mathbb {P}_{\omega _2}}\vDash \mathfrak {a}_T=\mathfrak {u}=\omega _2$
. The iteration
![]() ${\mathbb {P}_{\omega _2}}$
has the Sacks property and therefore
${\mathbb {P}_{\omega _2}}$
has the Sacks property and therefore
![]() $\operatorname {\mathrm {cof}}(\mathcal {N})=\omega _1$
. By the indestructibility of selective independence the family
$\operatorname {\mathrm {cof}}(\mathcal {N})=\omega _1$
. By the indestructibility of selective independence the family
![]() $\mathcal {A}_0$
remains maximal independent in
$\mathcal {A}_0$
remains maximal independent in
![]() $V^{\mathbb {P}_{\omega _2}}$
and so a witness to
$V^{\mathbb {P}_{\omega _2}}$
and so a witness to
![]() $\mathfrak {i}=\omega _1$
. Moreover, by the preservation properties of tight MAD families (see [Reference Guzmán, Hrušák and Téllez25]), and the above preservation theorems,
$\mathfrak {i}=\omega _1$
. Moreover, by the preservation properties of tight MAD families (see [Reference Guzmán, Hrušák and Téllez25]), and the above preservation theorems,
![]() $\mathcal {A}_1$
is a witness to
$\mathcal {A}_1$
is a witness to
![]() $\mathfrak {a}=\omega _1$
in the final model.
$\mathfrak {a}=\omega _1$
in the final model.
6 Appendix: The problem of Vaughan
We conclude the paper with an overview of the problem of Vaughan and point many of the difficulties surrounding a possible solution of it, in particular the fact that the most common forcing methods do not seem to help with the problem:
-
(1) Finite support iteration of ccc forcings of length a regular cardinal over a model of CH. This approach cannot work since in the models obtained in this way, the size of the continuum is equal to
 $cov\left ( \mathcal {M}\right )$
and it is known that
$cov\left ( \mathcal {M}\right )$
and it is known that
 $cov\left ( \mathcal {M}\right ) \leq \mathfrak {i}$
.Footnote
5
$cov\left ( \mathcal {M}\right ) \leq \mathfrak {i}$
.Footnote
5
-
(2) Countable support iteration of definable proper forcings of length
 $\omega _{2}$
over a model of CH
. It follows by the results of Džamonja, Hrušák, and Moore in [Reference Moore, Hrušák and Džamonja43] that in all of these models the equality
$\omega _{2}$
over a model of CH
. It follows by the results of Džamonja, Hrušák, and Moore in [Reference Moore, Hrušák and Džamonja43] that in all of these models the equality
 $\mathfrak {b=a}$
will hold, so in particular we will have that
$\mathfrak {b=a}$
will hold, so in particular we will have that
 $\mathfrak {a\leq i}$
.
$\mathfrak {a\leq i}$
. -
(3) Countable support iteration of non-definable proper forcings of length
 $\omega _{2}$
over a model of CH. This approach could work; however a model of
$\omega _{2}$
over a model of CH. This approach could work; however a model of
 $\mathfrak {i<a}$
obtained by this method will also be a model of
$\mathfrak {i<a}$
obtained by this method will also be a model of
 $\omega _{1}=\mathfrak {d<a}$
(since
$\omega _{1}=\mathfrak {d<a}$
(since
 $\mathfrak {d}\leq \mathfrak {i}$
), thus solving the problem of Roitman, which is considered to be one of the hardest problems in the theory of cardinal invariants.
$\mathfrak {d}\leq \mathfrak {i}$
), thus solving the problem of Roitman, which is considered to be one of the hardest problems in the theory of cardinal invariants. -
(4) Forcing with ultrapowers and iterating along a template. The method of forcing with ultrapowers and iterating along a template was introduced by Shelah in [Reference Shelah48] to build models of
 $\mathfrak {d<a}$
and
$\mathfrak {d<a}$
and
 $\mathfrak {u<a}$
. This is a very powerful method that has been very useful and has been successfully applied to this day. Unfortunately, it seems that all forcings obtained using this method tend to increase
$\mathfrak {u<a}$
. This is a very powerful method that has been very useful and has been successfully applied to this day. Unfortunately, it seems that all forcings obtained using this method tend to increase
 $\mathfrak {i}$
for the same reason they increase
$\mathfrak {i}$
for the same reason they increase
 $\mathfrak {a.}$
To learn more about this powerful method, see [Reference Brendle8–Reference Brendle10, Reference Fischer and Mejía16, Reference Fischer and Törnquist20, Reference Fischer, Friedman, Mejía and Montoya22, Reference Mejía39].
$\mathfrak {a.}$
To learn more about this powerful method, see [Reference Brendle8–Reference Brendle10, Reference Fischer and Mejía16, Reference Fischer and Törnquist20, Reference Fischer, Friedman, Mejía and Montoya22, Reference Mejía39]. -
(5) Short finite support iterations over models of MA. Performing a finite support iteration of length
 $\omega _{1}$
over a model of MA (for example) is a powerful method to add “small witnesses” of some cardinal invariants while keeping others large. Models obtained in this way are often called “dual models” (see [Reference Brendle and Flašková12] for several interesting results and applications of these methods). In [Reference Balcar, Hernández-Hernández and Hrušák2] a dual model was constructed to add a small maximal independent family in order to build a model of
$\omega _{1}$
over a model of MA (for example) is a powerful method to add “small witnesses” of some cardinal invariants while keeping others large. Models obtained in this way are often called “dual models” (see [Reference Brendle and Flašková12] for several interesting results and applications of these methods). In [Reference Balcar, Hernández-Hernández and Hrušák2] a dual model was constructed to add a small maximal independent family in order to build a model of
 $\mathfrak {i<} non\left ( \mathcal {N}\right )$
. Unfortunately, it is not clear how one could avoid adding a small MAD family with this method. Moreover, it seems likely that the principle
$\mathfrak {i<} non\left ( \mathcal {N}\right )$
. Unfortunately, it is not clear how one could avoid adding a small MAD family with this method. Moreover, it seems likely that the principle
 $\Diamond _{\mathfrak {d}}$
of Hrušák will hold in these modelsFootnote
6
(see [Reference Hrušák28]).
$\Diamond _{\mathfrak {d}}$
of Hrušák will hold in these modelsFootnote
6
(see [Reference Hrušák28]).
In principle, it could be possible to construct a model of
![]() $\mathfrak {i<a}$
using matrix iterations (see [Reference Blass and Shelah7, Reference Brendle and Fischer11, Reference Mejía38] to learn more about this method), but one would need to be very careful in order to avoid problems like in the points 1 and 5 above.
$\mathfrak {i<a}$
using matrix iterations (see [Reference Blass and Shelah7, Reference Brendle and Fischer11, Reference Mejía38] to learn more about this method), but one would need to be very careful in order to avoid problems like in the points 1 and 5 above.
Acknowledgements
The authors would like to thank Michael Hrušák for his valuable comments regarding the topic of the paper and the anonymous referee for many helpful comments which significantly improved the quality of the manuscript. The first and third authors gratefully acknowledge support from PAPIIT grant IA102222 and CANACyT grant A1-S-16164. The second author would like to thank the Austrian Science Fund (FWF) for the generous support through grant number Y1012-N35 (Fischer). The fourth author would like to thank the Austrian Agency for International Cooperation in Education and Research (OeAD-GmbH) for the scholarship ICM-2020-00442 in the frame of Aktion Österreich-Slowakei, AÖSK-Stipendien für Postdoktoranden, as well as Slovak Research and Development Agency for grant APVV-16-0337.