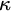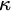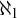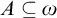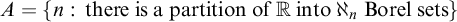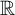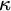1 Introduction
By work of Lusin and Sierpiński in [Reference Lusin and Sierpiński16], there is an analytic, non-Borel subset of
![]() $\mathbb {R}$
, and every analytic and every coanalytic set is the union of
$\mathbb {R}$
, and every analytic and every coanalytic set is the union of
![]() $\aleph _1$
Borel sets. It follows that
$\aleph _1$
Borel sets. It follows that
![]() $\mathbb {R}$
can be partitioned into
$\mathbb {R}$
can be partitioned into
![]() $\aleph _1$
Borel sets. Hausdorff later sharpened this in [Reference Hausdorff10], showing that
$\aleph _1$
Borel sets. Hausdorff later sharpened this in [Reference Hausdorff10], showing that
![]() $\mathbb {R}$
, or any other uncountable Polish space, can be written as an increasing union of
$\mathbb {R}$
, or any other uncountable Polish space, can be written as an increasing union of
![]() $\aleph _1 G_{\delta }$
sets, and therefore can be partitioned into
$\aleph _1 G_{\delta }$
sets, and therefore can be partitioned into
![]() $\aleph _1 F_{\sigma \delta }$
sets. This raises the question:
$\aleph _1 F_{\sigma \delta }$
sets. This raises the question:
-
(Q1) For which uncountable cardinals
 $\kappa $
is there a partition of
$\kappa $
is there a partition of
 $\mathbb {R}$
into
$\mathbb {R}$
into
 $\kappa $
nonempty Borel sets?
$\kappa $
nonempty Borel sets?
Let us define the Borel partition spectrum, denoted
![]() $\mathfrak {sp}({\small\text{Borel}})$
, to be the answer to this question:
$\mathfrak {sp}({\small\text{Borel}})$
, to be the answer to this question:
The main result of this paper shows that the Borel partition spectrum can be fairly arbitrary. (A precise statement of the result can be found in Corollary 3.3.) For example, given any set A of positive integers, there is a forcing extension in which
![]() $\mathfrak {sp}({\small\text{Borel}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _1,\aleph _{\omega },\aleph _{\omega +1}\}$
.
$\mathfrak {sp}({\small\text{Borel}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _1,\aleph _{\omega },\aleph _{\omega +1}\}$
.
A related question can be asked for any given class of subsets of
![]() $\mathbb {R}$
. As
$\mathbb {R}$
. As
![]() $\mathbb {R}$
is connected, there is no partition of
$\mathbb {R}$
is connected, there is no partition of
![]() $\mathbb {R}$
into two or more open sets. So the descriptively simplest sets one can ask this for are the closed sets.
$\mathbb {R}$
into two or more open sets. So the descriptively simplest sets one can ask this for are the closed sets.
-
(Q2) For which cardinals
 $\kappa $
is there a partition of
$\kappa $
is there a partition of
 $\mathbb {R}$
into
$\mathbb {R}$
into
 $\kappa $
closed sets?
$\kappa $
closed sets?
Making use of the Baire Category Theorem, Sierpiński proved in [Reference Sierpiński23] that any partition of
![]() $\mathbb {R}$
into at least two nonempty closed sets is uncountable. (Using the modern vocabulary, his proof actually shows that any partition of
$\mathbb {R}$
into at least two nonempty closed sets is uncountable. (Using the modern vocabulary, his proof actually shows that any partition of
![]() $\mathbb {R}$
into closed sets has size
$\mathbb {R}$
into closed sets has size
![]() $\geq \!\mathrm {cov}(\mathcal M)$
.) Let us define the closed partition spectrum, denoted
$\geq \!\mathrm {cov}(\mathcal M)$
.) Let us define the closed partition spectrum, denoted
![]() $\mathfrak {sp}({\small\text{closed}})$
, to be the answer to (Q2):
$\mathfrak {sp}({\small\text{closed}})$
, to be the answer to (Q2):
We show that, like the Borel partition spectrum,
![]() $\mathfrak {sp}({\small\text{closed}})$
can be fairly arbitrary—even more so, in fact, since the closed partition spectrum need not contain
$\mathfrak {sp}({\small\text{closed}})$
can be fairly arbitrary—even more so, in fact, since the closed partition spectrum need not contain
![]() $\aleph _1$
. For example, given any nonempty
$\aleph _1$
. For example, given any nonempty
![]() $A \subseteq \omega \setminus \{0\}$
, there is a forcing extension in which
$A \subseteq \omega \setminus \{0\}$
, there is a forcing extension in which
![]() $\mathfrak {sp}({\small\text{closed}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _{\omega },\aleph _{\omega +1}\}$
.
$\mathfrak {sp}({\small\text{closed}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _{\omega },\aleph _{\omega +1}\}$
.
These results about
![]() $\mathfrak {sp}({\small\text{Borel}})$
and
$\mathfrak {sp}({\small\text{Borel}})$
and
![]() $\mathfrak {sp}({\small\text{closed}})$
are encompassed in a single theorem, Theorem 3.2. The proof identifies a notion of forcing that adds partitions of
$\mathfrak {sp}({\small\text{closed}})$
are encompassed in a single theorem, Theorem 3.2. The proof identifies a notion of forcing that adds partitions of
![]() $\mathbb {R}$
into closed sets having certain prescribed sizes, while avoiding partitions of
$\mathbb {R}$
into closed sets having certain prescribed sizes, while avoiding partitions of
![]() $\mathbb {R}$
into Borel sets with other sizes. The second of these tasks is the more difficult. It is accomplished via an isomorphism-of-names argument, similar to the folklore proof (found, e.g., in [Reference Brendle3, Theorem 3.1]) that, after many mutually generic Cohen reals are added to a model of
$\mathbb {R}$
into Borel sets with other sizes. The second of these tasks is the more difficult. It is accomplished via an isomorphism-of-names argument, similar to the folklore proof (found, e.g., in [Reference Brendle3, Theorem 3.1]) that, after many mutually generic Cohen reals are added to a model of
![]() $\mathsf {CH}$
, there are no MAD families of size strictly between
$\mathsf {CH}$
, there are no MAD families of size strictly between
![]() $\aleph _1$
and
$\aleph _1$
and
![]() $\mathfrak {c}$
.
$\mathfrak {c}$
.
Let us point out that analogues of (Q1) and (Q2) have been asked and answered (or partly answered) concerning other extremal families. For example, consider
![]() $\mathfrak {sp}({\scriptstyle\text{MAD}}) = \left \lbrace \kappa \geq \aleph _0 \colon \text {there is a MAD family of size } \kappa \right \rbrace $
. Hechler showed in [Reference Hechler11] that
$\mathfrak {sp}({\scriptstyle\text{MAD}}) = \left \lbrace \kappa \geq \aleph _0 \colon \text {there is a MAD family of size } \kappa \right \rbrace $
. Hechler showed in [Reference Hechler11] that
![]() $\mathfrak {sp}({\scriptstyle\text{MAD}})$
can include any prescribed set of cardinals, and Blass showed in [Reference Blass and Judah2] how to exclude certain cardinals from
$\mathfrak {sp}({\scriptstyle\text{MAD}})$
can include any prescribed set of cardinals, and Blass showed in [Reference Blass and Judah2] how to exclude certain cardinals from
![]() $\mathfrak {sp}({\scriptstyle\text{MAD}})$
. Shelah and Spinas proved the strongest results in [Reference Shelah and Spinas22], showing that
$\mathfrak {sp}({\scriptstyle\text{MAD}})$
. Shelah and Spinas proved the strongest results in [Reference Shelah and Spinas22], showing that
![]() $\mathfrak {sp}({\scriptstyle\text{MAD}})$
can be rather arbitrary, especially on the regular cardinals. Similarly, the spectrum of possible sizes of maximal independent families,
$\mathfrak {sp}({\scriptstyle\text{MAD}})$
can be rather arbitrary, especially on the regular cardinals. Similarly, the spectrum of possible sizes of maximal independent families,
![]() $\mathfrak {sp}({\small\text{mif}})$
, was investigated recently by Fischer and Shelah in [Reference Fischer and Shelah7, Reference Fischer and Shelah8]. Like with
$\mathfrak {sp}({\small\text{mif}})$
, was investigated recently by Fischer and Shelah in [Reference Fischer and Shelah7, Reference Fischer and Shelah8]. Like with
![]() $\mathfrak {sp}({\scriptstyle\text{MAD}})$
, they proved that
$\mathfrak {sp}({\scriptstyle\text{MAD}})$
, they proved that
![]() $\mathfrak {sp}({\small\text{mif}})$
can be fairly arbitrary, especially on the regular cardinals. Similar work concerning maximal cofinitary groups was done by Fischer in [Reference Fischer6]. Ultimately, all these proofs share the same core idea: variations on the isomorphism-of-names argument mentioned above. In every case, the key to making this kind of argument work is to find an automorphism-rich poset that can be used to add extremal families of prescribed sizes. One notable exception to this rule is Shelah’s analysis of the set of possible sizes of ultrafilter bases in [Reference Shelah21], where he proves, from large cardinal hypotheses, that this spectrum can exhibit fairly chaotic behavior.
$\mathfrak {sp}({\small\text{mif}})$
can be fairly arbitrary, especially on the regular cardinals. Similar work concerning maximal cofinitary groups was done by Fischer in [Reference Fischer6]. Ultimately, all these proofs share the same core idea: variations on the isomorphism-of-names argument mentioned above. In every case, the key to making this kind of argument work is to find an automorphism-rich poset that can be used to add extremal families of prescribed sizes. One notable exception to this rule is Shelah’s analysis of the set of possible sizes of ultrafilter bases in [Reference Shelah21], where he proves, from large cardinal hypotheses, that this spectrum can exhibit fairly chaotic behavior.
2
 $\mathfrak {sp}({\small\text{Borel}})$
and
$\mathfrak {sp}({\small\text{Borel}})$
and
 $\mathfrak {sp}({\small\text{closed}})$
do not depend on
$\mathfrak {sp}({\small\text{closed}})$
do not depend on
 $\mathbb {R}$
$\mathbb {R}$
We begin this section by observing that the definition of
![]() $\mathfrak {sp}({\small\text{Borel}})$
does not depend on
$\mathfrak {sp}({\small\text{Borel}})$
does not depend on
![]() $\mathbb {R}$
, and remains unchanged when
$\mathbb {R}$
, and remains unchanged when
![]() $\mathbb {R}$
is replaced by any other uncountable Polish space:
$\mathbb {R}$
is replaced by any other uncountable Polish space:
Theorem 2.1. If X is any uncountable Polish space, then
Proof By a theorem of Kuratowski (see [Reference Kechris14, Theorem 15.6]), any two uncountable Polish spaces are Borel isomorphic: in other words, there is a bijection
![]() $f: \mathbb {R} \to X$
such that
$f: \mathbb {R} \to X$
such that
![]() $A \subseteq \mathbb {R}$
is Borel if and only if
$A \subseteq \mathbb {R}$
is Borel if and only if
![]() $f[A]$
is Borel. Thus if
$f[A]$
is Borel. Thus if
![]() $\mathcal {P}$
is any partition of
$\mathcal {P}$
is any partition of
![]() $\mathbb {R}$
into Borel sets, then
$\mathbb {R}$
into Borel sets, then
![]() $\left \lbrace f[B] \colon B \in \mathcal {P} \right \rbrace $
is a partition of X into Borel sets, and if
$\left \lbrace f[B] \colon B \in \mathcal {P} \right \rbrace $
is a partition of X into Borel sets, and if
![]() $\mathcal Q$
is any partition of X into Borel sets, then
$\mathcal Q$
is any partition of X into Borel sets, then
![]() $\left \lbrace f^{-1}[B] \colon B \in \mathcal Q \right \rbrace $
is a partition of
$\left \lbrace f^{-1}[B] \colon B \in \mathcal Q \right \rbrace $
is a partition of
![]() $\mathbb {R}$
into Borel sets.
$\mathbb {R}$
into Borel sets.
It turns out that the same is true for
![]() $\mathfrak {sp}({\small\text{closed}})$
: if X is any uncountable Polish space, then
$\mathfrak {sp}({\small\text{closed}})$
: if X is any uncountable Polish space, then
A related theorem is proved by Miller in [Reference Miller, Barwise, Keisler and Kunen17, Theorem 3]:
![]() $\mathbb {R}$
can be partitioned into
$\mathbb {R}$
can be partitioned into
![]() $\aleph _1$
closed sets if and only if some uncountable Polish space can be, if and only if every uncountable Polish space can be. We wish to prove the same, but with an arbitrary uncountable cardinal
$\aleph _1$
closed sets if and only if some uncountable Polish space can be, if and only if every uncountable Polish space can be. We wish to prove the same, but with an arbitrary uncountable cardinal
![]() $\kappa $
in place of
$\kappa $
in place of
![]() $\aleph _1$
. Miller’s proof does not readily adapt to this task, because it uses in an essential way the fact that
$\aleph _1$
. Miller’s proof does not readily adapt to this task, because it uses in an essential way the fact that
![]() $\aleph _1$
is the smallest uncountable cardinal. So we take a different approach. First we need a few lemmas.
$\aleph _1$
is the smallest uncountable cardinal. So we take a different approach. First we need a few lemmas.
Lemma 2.2. For any uncountable cardinal
![]() $\kappa $
, the following are equivalent:
$\kappa $
, the following are equivalent:
-
(1) There is a partition of
 $2^{\omega }$
into
$2^{\omega }$
into
 $\kappa $
closed sets.
$\kappa $
closed sets. -
(2) There is a partition of
 $\omega ^{\omega }$
into
$\omega ^{\omega }$
into
 $\kappa $
compact sets.
$\kappa $
compact sets. -
(3) For every uncountable Polish space X, there is a partition of X into
 $\kappa $
compact sets.
$\kappa $
compact sets. -
(4) For some uncountable compact Polish space X, there is a partition of X into
 $\kappa F_{\sigma }$
sets.
$\kappa F_{\sigma }$
sets.
Proof Throughout the proof, if
![]() $X \subseteq Y$
and
$X \subseteq Y$
and
![]() $\mathcal {P}$
is a partition of Y, then
$\mathcal {P}$
is a partition of Y, then
![]() $\mathcal {P} \!\restriction \! X = \left \lbrace K \cap X \colon K \in \mathcal {P} \right \rbrace $
denotes the restriction of
$\mathcal {P} \!\restriction \! X = \left \lbrace K \cap X \colon K \in \mathcal {P} \right \rbrace $
denotes the restriction of
![]() $\mathcal {P}$
to X. We prove that
$\mathcal {P}$
to X. We prove that
![]() $(1) \Rightarrow (2) \Rightarrow (3) \Rightarrow (4) \Rightarrow (1)$
.
$(1) \Rightarrow (2) \Rightarrow (3) \Rightarrow (4) \Rightarrow (1)$
.
![]() $(1) \Rightarrow (2)$
: Suppose
$(1) \Rightarrow (2)$
: Suppose
![]() $\mathcal {P}$
is a partition of
$\mathcal {P}$
is a partition of
![]() $2^{\omega }$
into
$2^{\omega }$
into
![]() $\kappa $
closed sets. We claim first that there is a closed
$\kappa $
closed sets. We claim first that there is a closed
![]() $X \subseteq 2^{\omega }$
such that
$X \subseteq 2^{\omega }$
such that
![]() $\mathcal {P} \!\restriction \! X$
is a partition of X into
$\mathcal {P} \!\restriction \! X$
is a partition of X into
![]() $\kappa $
nowhere dense closed sets (nowhere dense in X, that is).
$\kappa $
nowhere dense closed sets (nowhere dense in X, that is).
To see this, we define a descending transfinite sequence of closed subsets of
![]() $2^{\omega }$
. Let
$2^{\omega }$
. Let
![]() $X_0 = 2^{\omega }$
, and if
$X_0 = 2^{\omega }$
, and if
![]() $\alpha $
is a limit ordinal, take
$\alpha $
is a limit ordinal, take
![]() $X_{\alpha } = \bigcap _{\xi < \alpha }X_{\xi }$
. At stage
$X_{\alpha } = \bigcap _{\xi < \alpha }X_{\xi }$
. At stage
![]() $\alpha $
, given
$\alpha $
, given
![]() $X_{\alpha }$
, form
$X_{\alpha }$
, form
![]() $X_{\alpha +1}$
by removing any open subset of
$X_{\alpha +1}$
by removing any open subset of
![]() $X_{\alpha }$
contained in a single member of
$X_{\alpha }$
contained in a single member of
![]() $\mathcal {P}$
:
$\mathcal {P}$
:
![]() $X_{\alpha +1} = X_{\alpha } \setminus \bigcup \left \lbrace U \colon U \text { is open in }X_{\alpha } \text { and } \left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! U \right \rvert = 1 \right \rbrace $
. Because
$X_{\alpha +1} = X_{\alpha } \setminus \bigcup \left \lbrace U \colon U \text { is open in }X_{\alpha } \text { and } \left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! U \right \rvert = 1 \right \rbrace $
. Because
![]() $2^{\omega }$
is second countable, there is some
$2^{\omega }$
is second countable, there is some
![]() $\beta < \omega _1$
such that
$\beta < \omega _1$
such that
![]() $X_{\beta } = X_{\gamma }$
for all
$X_{\beta } = X_{\gamma }$
for all
![]() $\gamma \geq \beta $
. Let
$\gamma \geq \beta $
. Let
![]() $X = X_{\beta }$
. Clearly,
$X = X_{\beta }$
. Clearly,
![]() $\mathcal {P} \!\restriction \! X$
is a partition of X into compact nowhere dense sets. Furthermore, at any stage
$\mathcal {P} \!\restriction \! X$
is a partition of X into compact nowhere dense sets. Furthermore, at any stage
![]() $\alpha < \beta $
of our recursion,
$\alpha < \beta $
of our recursion,
![]() $\left \lbrace K \in \mathcal {P} \colon K \cap X_{\alpha } \neq K \cap X_{\alpha +1} \right \rbrace $
is countable. Thus
$\left \lbrace K \in \mathcal {P} \colon K \cap X_{\alpha } \neq K \cap X_{\alpha +1} \right \rbrace $
is countable. Thus
![]() $\left \lbrace K \in \mathcal {P} \colon K \cap X \neq K \right \rbrace $
is countable. It follows that
$\left \lbrace K \in \mathcal {P} \colon K \cap X \neq K \right \rbrace $
is countable. It follows that
![]() $\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! X \right \rvert = \left \lvert \mathcal {P} \right \rvert = \kappa $
.
$\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! X \right \rvert = \left \lvert \mathcal {P} \right \rvert = \kappa $
.
Now, we claim there is a subspace Y of X such that
![]() $Y \approx \omega ^{\omega }$
and
$Y \approx \omega ^{\omega }$
and
![]() $\mathcal {P} \!\restriction \! Y$
is a partition of Y into
$\mathcal {P} \!\restriction \! Y$
is a partition of Y into
![]() $\kappa $
compact sets. Fix a countable basis
$\kappa $
compact sets. Fix a countable basis
![]() $\mathcal {B}$
for X, and for every
$\mathcal {B}$
for X, and for every
![]() $U \in \mathcal {B}$
fix some
$U \in \mathcal {B}$
fix some
![]() $K_U \in \mathcal {P}$
such that
$K_U \in \mathcal {P}$
such that
![]() $K_U \cap U \neq \emptyset $
. Let
$K_U \cap U \neq \emptyset $
. Let
![]() $Y = X \setminus \bigcup \left \lbrace K_U \colon U \in \mathcal {B} \right \rbrace $
. Clearly
$Y = X \setminus \bigcup \left \lbrace K_U \colon U \in \mathcal {B} \right \rbrace $
. Clearly
![]() $\mathcal {P} \!\restriction \! Y = \mathcal {P} \setminus \left \lbrace K_U \colon U \in \mathcal {B} \right \rbrace $
, so
$\mathcal {P} \!\restriction \! Y = \mathcal {P} \setminus \left \lbrace K_U \colon U \in \mathcal {B} \right \rbrace $
, so
![]() $\mathcal {P}$
partitions Y into
$\mathcal {P}$
partitions Y into
![]() $\kappa $
compact sets. The set
$\kappa $
compact sets. The set
![]() $\left \lbrace K_U \colon U \in \mathcal {B} \right \rbrace $
is both dense and meager in X. It follows that no relatively (cl)open subset of Y is closed in X, and therefore no (cl)open subset of Y is compact. Furthermore Y is
$\left \lbrace K_U \colon U \in \mathcal {B} \right \rbrace $
is both dense and meager in X. It follows that no relatively (cl)open subset of Y is closed in X, and therefore no (cl)open subset of Y is compact. Furthermore Y is
![]() $G_{\delta }$
in X, and therefore Polish. That
$G_{\delta }$
in X, and therefore Polish. That
![]() $Y \approx \omega ^{\omega }$
now follows from the Alexander–Urysohn characterization of
$Y \approx \omega ^{\omega }$
now follows from the Alexander–Urysohn characterization of
![]() $\omega ^{\omega }$
as the unique nowhere compact, zero-dimensional Polish space (see [Reference Kechris14, Theorem 7.7]).
$\omega ^{\omega }$
as the unique nowhere compact, zero-dimensional Polish space (see [Reference Kechris14, Theorem 7.7]).
![]() $(2) \Rightarrow (3)$
: Suppose
$(2) \Rightarrow (3)$
: Suppose
![]() $\mathcal {P}$
is a partition of
$\mathcal {P}$
is a partition of
![]() $\omega ^{\omega }$
into
$\omega ^{\omega }$
into
![]() $\kappa $
compact sets, and let X be any uncountable Polish space. Decompose X into its scattered part and perfect part: i.e., let
$\kappa $
compact sets, and let X be any uncountable Polish space. Decompose X into its scattered part and perfect part: i.e., let
![]() $X = Y \cup Z$
, where Y is countable and Z is closed in X (hence still Polish) and Z has no isolated points. By [Reference Kechris14, Exercise 7.15], there is a continuous bijection
$X = Y \cup Z$
, where Y is countable and Z is closed in X (hence still Polish) and Z has no isolated points. By [Reference Kechris14, Exercise 7.15], there is a continuous bijection
![]() $f: \omega ^{\omega } \to Z$
. But then
$f: \omega ^{\omega } \to Z$
. But then
![]() $\left \lbrace f[K] \colon K \in \mathcal {P} \right \rbrace \cup \left \lbrace \{y\} \colon y \in Y \right \rbrace $
is a partition of X into
$\left \lbrace f[K] \colon K \in \mathcal {P} \right \rbrace \cup \left \lbrace \{y\} \colon y \in Y \right \rbrace $
is a partition of X into
![]() $\kappa $
compact sets.
$\kappa $
compact sets.
![]() $(3) \Rightarrow (4)$
: This implication is obvious, since “every uncountable Polish space” includes some compact spaces, and compact sets are
$(3) \Rightarrow (4)$
: This implication is obvious, since “every uncountable Polish space” includes some compact spaces, and compact sets are
![]() $F_{\sigma }$
.
$F_{\sigma }$
.
![]() $(4) \Rightarrow (1)$
: Suppose X is an uncountable compact Polish space. By [Reference Kechris14, Theorem 7.4], there is a continuous surjection
$(4) \Rightarrow (1)$
: Suppose X is an uncountable compact Polish space. By [Reference Kechris14, Theorem 7.4], there is a continuous surjection
![]() $f: 2^{\omega } \to X$
. If
$f: 2^{\omega } \to X$
. If
![]() $\mathcal {P}$
is any partition of X into
$\mathcal {P}$
is any partition of X into
![]() $\kappa F_{\sigma }$
sets, then
$\kappa F_{\sigma }$
sets, then
![]() $\mathcal {Q} = \left \lbrace f^{-1}[K] \colon K \in \mathcal {P} \right \rbrace $
is a partition of
$\mathcal {Q} = \left \lbrace f^{-1}[K] \colon K \in \mathcal {P} \right \rbrace $
is a partition of
![]() $2^{\omega }$
into
$2^{\omega }$
into
![]() $\kappa F_{\sigma }$
sets. But every
$\kappa F_{\sigma }$
sets. But every
![]() $F_{\sigma }$
subset of
$F_{\sigma }$
subset of
![]() $2^{\omega }$
can be partitioned into countably many closed sets. (This observation is attributed to Luzin in [Reference Miller, Barwise, Keisler and Kunen17, Theorem 2].) Thus, by breaking up any non-closed members of
$2^{\omega }$
can be partitioned into countably many closed sets. (This observation is attributed to Luzin in [Reference Miller, Barwise, Keisler and Kunen17, Theorem 2].) Thus, by breaking up any non-closed members of
![]() $\mathcal Q$
into countably many closed pieces, we can refine
$\mathcal Q$
into countably many closed pieces, we can refine
![]() $\mathcal Q$
to obtain a partition of
$\mathcal Q$
to obtain a partition of
![]() $2^{\omega }$
into
$2^{\omega }$
into
![]() $\kappa $
closed sets.
$\kappa $
closed sets.
Define the Sierpiński cardinal
![]() $\acute {\mathfrak {n}}$
to be the minimum size of a cardinal satisfying the equivalent statements in Lemma 2.2: that is,
$\acute {\mathfrak {n}}$
to be the minimum size of a cardinal satisfying the equivalent statements in Lemma 2.2: that is,
 $$ \begin{align*} \acute{\mathfrak{n}} \,&= \min \left\lbrace |\mathcal{P}| \colon \mathcal{P} \text{ is a partition of } 2^{\omega} \text{ into uncountably many closed sets} \right\rbrace \\ &= \min \left\lbrace |\mathcal{P}| \colon \mathcal{P} \text{ is a partition of } \omega^{\omega} \text{ into compact sets} \right\rbrace. \end{align*} $$
$$ \begin{align*} \acute{\mathfrak{n}} \,&= \min \left\lbrace |\mathcal{P}| \colon \mathcal{P} \text{ is a partition of } 2^{\omega} \text{ into uncountably many closed sets} \right\rbrace \\ &= \min \left\lbrace |\mathcal{P}| \colon \mathcal{P} \text{ is a partition of } \omega^{\omega} \text{ into compact sets} \right\rbrace. \end{align*} $$
Recall that the dominating number
![]() ${\mathfrak d}$
is equal to the smallest covering of
${\mathfrak d}$
is equal to the smallest covering of
![]() $\omega ^{\omega }$
by compact sets. Hence
$\omega ^{\omega }$
by compact sets. Hence
![]() ${\mathfrak d} \leq \acute {\mathfrak {n}}$
. And clearly
${\mathfrak d} \leq \acute {\mathfrak {n}}$
. And clearly
![]() $\acute {\mathfrak {n}} \leq \mathfrak {c}$
, because
$\acute {\mathfrak {n}} \leq \mathfrak {c}$
, because
![]() $\omega ^{\omega }$
can be partitioned into singletons. Thus we may consider
$\omega ^{\omega }$
can be partitioned into singletons. Thus we may consider
![]() $\acute {\mathfrak {n}}$
to be a cardinal characteristic of the continuum. Quite a bit is known already about this cardinal. The main results are due to Stern [Reference Stern25], Miller [Reference Miller, Barwise, Keisler and Kunen17], Newelski [Reference Newelski19], and Spinas [Reference Spinas24], who studied this cardinal implicitly without giving it a name, and Hrušak [Reference Hrušák12, Reference Hrušák13], who denotes it
$\acute {\mathfrak {n}}$
to be a cardinal characteristic of the continuum. Quite a bit is known already about this cardinal. The main results are due to Stern [Reference Stern25], Miller [Reference Miller, Barwise, Keisler and Kunen17], Newelski [Reference Newelski19], and Spinas [Reference Spinas24], who studied this cardinal implicitly without giving it a name, and Hrušak [Reference Hrušák12, Reference Hrušák13], who denotes it
![]() $\mathfrak {a}_T$
. The name “Sierpiński cardinal” and the notation
$\mathfrak {a}_T$
. The name “Sierpiński cardinal” and the notation
![]() $\acute {\mathfrak {n}}$
were suggested by Banakh in [Reference Banakh1].
$\acute {\mathfrak {n}}$
were suggested by Banakh in [Reference Banakh1].
A set S of cardinals is closed under singular limits if for every singular cardinal
![]() $\kappa $
, if
$\kappa $
, if
![]() $S \cap \kappa $
is unbounded in
$S \cap \kappa $
is unbounded in
![]() $\kappa $
, then
$\kappa $
, then
![]() $\kappa \in S$
.
$\kappa \in S$
.
Lemma 2.3. The set
![]() $S = \left \lbrace \kappa \colon \text {there is a partition of } 2^{\omega } \text { into }\kappa \text { closed sets} \right \rbrace $
is closed under singular limits.
$S = \left \lbrace \kappa \colon \text {there is a partition of } 2^{\omega } \text { into }\kappa \text { closed sets} \right \rbrace $
is closed under singular limits.
Proof Suppose
![]() $\kappa $
is a singular cardinal and
$\kappa $
is a singular cardinal and
![]() $S \cap \kappa $
is unbounded in
$S \cap \kappa $
is unbounded in
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\nu = \mathrm {cf}(\kappa ) < \kappa $
, and let
$\nu = \mathrm {cf}(\kappa ) < \kappa $
, and let
![]() $\left \langle \alpha _{\xi } \colon \xi < \nu \right \rangle $
be a sequence of cardinals in S increasing up to
$\left \langle \alpha _{\xi } \colon \xi < \nu \right \rangle $
be a sequence of cardinals in S increasing up to
![]() $\kappa $
. Fix some
$\kappa $
. Fix some
![]() $\lambda \in S$
with
$\lambda \in S$
with
![]() $\nu \leq \lambda < \kappa $
.
$\nu \leq \lambda < \kappa $
.
Let
![]() $\left \lbrace K_{\xi } \colon \xi < \lambda \right \rbrace $
be a partition of
$\left \lbrace K_{\xi } \colon \xi < \lambda \right \rbrace $
be a partition of
![]() $2^{\omega }$
into closed sets. Observe that
$2^{\omega }$
into closed sets. Observe that
![]() $\left \lbrace 2^{\omega } \times K_{\xi } \colon \xi < \lambda \right \rbrace $
is a partition of
$\left \lbrace 2^{\omega } \times K_{\xi } \colon \xi < \lambda \right \rbrace $
is a partition of
![]() $2^{\omega } \times 2^{\omega } \approx 2^{\omega }$
into
$2^{\omega } \times 2^{\omega } \approx 2^{\omega }$
into
![]() $\lambda $
copies of
$\lambda $
copies of
![]() $2^{\omega }$
. Thus we may (and do) assume that
$2^{\omega }$
. Thus we may (and do) assume that
![]() $K_{\xi } \approx 2^{\omega }$
for each
$K_{\xi } \approx 2^{\omega }$
for each
![]() $\xi < \lambda $
. For each
$\xi < \lambda $
. For each
![]() $\xi < \nu $
, let
$\xi < \nu $
, let
![]() $\mathcal {P}_{\xi }$
be a partition of
$\mathcal {P}_{\xi }$
be a partition of
![]() $K_{\xi }$
into
$K_{\xi }$
into
![]() $\alpha _{\xi }$
closed sets (using the fact that
$\alpha _{\xi }$
closed sets (using the fact that
![]() $\alpha _{\xi } \in S$
). Then
$\alpha _{\xi } \in S$
). Then
![]() $\bigcup _{\xi < \nu }\mathcal {P}_{\xi } \cup \left \lbrace K_{\xi } \colon \nu \leq \xi < \lambda \right \rbrace $
is a partition of
$\bigcup _{\xi < \nu }\mathcal {P}_{\xi } \cup \left \lbrace K_{\xi } \colon \nu \leq \xi < \lambda \right \rbrace $
is a partition of
![]() $2^{\omega }$
into
$2^{\omega }$
into
![]() $\kappa $
closed sets.
$\kappa $
closed sets.
Theorem 2.4. Let
![]() $\kappa $
be an uncountable cardinal. Then all six statements of the following form are equivalent:
$\kappa $
be an uncountable cardinal. Then all six statements of the following form are equivalent:
-
Some/every uncountable Polish space can be partitioned into
 $\kappa$
compact/closed/
$\kappa$
compact/closed/
 $F_{\sigma }$
sets.
$F_{\sigma }$
sets.
Proof It is clear that (every-compact)
![]() $\,\Rightarrow \,$
(every-closed)
$\,\Rightarrow \,$
(every-closed)
![]() $\,\Rightarrow \,$
(every-
$\,\Rightarrow \,$
(every-
![]() $F_{\sigma }$
), and that (some-compact)
$F_{\sigma }$
), and that (some-compact)
![]() $\,\Rightarrow \,$
(some-closed)
$\,\Rightarrow \,$
(some-closed)
![]() $\,\Rightarrow \,$
(some-
$\,\Rightarrow \,$
(some-
![]() $F_{\sigma }$
). Also, Lemma 2.2 implies that (every-
$F_{\sigma }$
). Also, Lemma 2.2 implies that (every-
![]() $F_{\sigma }$
)
$F_{\sigma }$
)
![]() $\,\Rightarrow \,$
(some-compact): because if every uncountable Polish space can be partitioned into
$\,\Rightarrow \,$
(some-compact): because if every uncountable Polish space can be partitioned into
![]() $\kappa F_{\sigma }$
sets, then in particular some uncountable compact Polish space can be, and by Lemma 2.2 this implies
$\kappa F_{\sigma }$
sets, then in particular some uncountable compact Polish space can be, and by Lemma 2.2 this implies
![]() $\omega ^{\omega }$
can be partitioned into
$\omega ^{\omega }$
can be partitioned into
![]() $\kappa $
compact sets. Thus, to prove the theorem, we need to show (some-
$\kappa $
compact sets. Thus, to prove the theorem, we need to show (some-
![]() $F_{\sigma }$
)
$F_{\sigma }$
)
![]() $\,\Rightarrow \,$
(every-compact).
$\,\Rightarrow \,$
(every-compact).
So let X be some uncountable Polish space, and suppose
![]() $\mathcal {P}$
is a partition of X into
$\mathcal {P}$
is a partition of X into
![]() $\kappa F_{\sigma }$
sets. If
$\kappa F_{\sigma }$
sets. If
![]() $\kappa = \acute {\mathfrak {n}}$
, then by definition, there is a partition of
$\kappa = \acute {\mathfrak {n}}$
, then by definition, there is a partition of
![]() $\omega ^{\omega }$
into
$\omega ^{\omega }$
into
![]() $\acute {\mathfrak {n}}$
compact sets, and by Lemma 2.2 every uncountable Polish space can be partitioned into
$\acute {\mathfrak {n}}$
compact sets, and by Lemma 2.2 every uncountable Polish space can be partitioned into
![]() $\kappa $
compact sets, and we are done. So let us suppose
$\kappa $
compact sets, and we are done. So let us suppose
![]() $\kappa> \acute {\mathfrak {n}}$
. We consider two cases.
$\kappa> \acute {\mathfrak {n}}$
. We consider two cases.
For the first case, suppose
![]() $\kappa $
is regular. By the definition of
$\kappa $
is regular. By the definition of
![]() $\acute {\mathfrak {n}}$
and Lemma 2.2, there is a partition
$\acute {\mathfrak {n}}$
and Lemma 2.2, there is a partition
![]() $\mathcal Q$
of X into
$\mathcal Q$
of X into
![]() $\acute {\mathfrak {n}}$
compact sets. Because
$\acute {\mathfrak {n}}$
compact sets. Because
![]() $|\mathcal {P}| = \kappa> \acute {\mathfrak {n}}$
and
$|\mathcal {P}| = \kappa> \acute {\mathfrak {n}}$
and
![]() $\kappa $
is regular, there is some
$\kappa $
is regular, there is some
![]() $K \in \mathcal Q$
such that
$K \in \mathcal Q$
such that
![]() $\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert = \kappa $
. Thus
$\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert = \kappa $
. Thus
![]() $\mathcal {P} \!\restriction \! K$
is a partition of K into
$\mathcal {P} \!\restriction \! K$
is a partition of K into
![]() $\kappa $
compact subsets. But K is a compact Polish space, and uncountable because
$\kappa $
compact subsets. But K is a compact Polish space, and uncountable because
![]() $|K| \geq \left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert = \kappa $
. Thus some compact uncountable Polish space can be partitioned into
$|K| \geq \left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert = \kappa $
. Thus some compact uncountable Polish space can be partitioned into
![]() $\kappa F_{\sigma }$
sets. Invoking Lemma 2.2 again, this implies every uncountable Polish space can be partitioned into
$\kappa F_{\sigma }$
sets. Invoking Lemma 2.2 again, this implies every uncountable Polish space can be partitioned into
![]() $\kappa $
compact sets.
$\kappa $
compact sets.
For the second case, suppose
![]() $\kappa $
is singular. As in the first case, there is a partition
$\kappa $
is singular. As in the first case, there is a partition
![]() $\mathcal Q$
of X into
$\mathcal Q$
of X into
![]() $\acute {\mathfrak {n}}$
compact sets. If
$\acute {\mathfrak {n}}$
compact sets. If
![]() $\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert = \kappa $
for some
$\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert = \kappa $
for some
![]() $K \in \mathcal Q$
, then we may argue as in the first case and conclude that every uncountable Polish space can be partitioned into
$K \in \mathcal Q$
, then we may argue as in the first case and conclude that every uncountable Polish space can be partitioned into
![]() $\kappa $
compact sets, and we are done. So let us suppose instead that
$\kappa $
compact sets, and we are done. So let us suppose instead that
![]() $\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert < \kappa $
for every
$\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert < \kappa $
for every
![]() $K \in \mathcal Q$
. Let
$K \in \mathcal Q$
. Let
![]() $\lambda $
be any cardinal with
$\lambda $
be any cardinal with
![]() $\acute {\mathfrak {n}} < \lambda < \kappa $
. Because
$\acute {\mathfrak {n}} < \lambda < \kappa $
. Because
![]() $|\mathcal {P}| = \kappa> \lambda > \acute {\mathfrak {n}} = |\mathcal Q|$
, there is some
$|\mathcal {P}| = \kappa> \lambda > \acute {\mathfrak {n}} = |\mathcal Q|$
, there is some
![]() $K \in \mathcal Q$
such that
$K \in \mathcal Q$
such that
![]() $\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert \geq \lambda $
. Let
$\left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert \geq \lambda $
. Let
![]() $\mu = \left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert $
, and note that
$\mu = \left \lvert \vphantom {f^f}\mathcal {P} \!\restriction \! K \right \rvert $
, and note that
![]() $\mu < \kappa $
(by the third sentence of this paragraph). Now, as in the previous paragraph, K is a compact uncountable Polish space that can be partitioned into
$\mu < \kappa $
(by the third sentence of this paragraph). Now, as in the previous paragraph, K is a compact uncountable Polish space that can be partitioned into
![]() $\mu F_{\sigma }$
sets. By Lemma 2.2, this implies
$\mu F_{\sigma }$
sets. By Lemma 2.2, this implies
![]() $2^{\omega }$
can be partitioned into
$2^{\omega }$
can be partitioned into
![]() $\mu $
closed sets. Because
$\mu $
closed sets. Because
![]() $\lambda $
was an arbitrary cardinal below
$\lambda $
was an arbitrary cardinal below
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda \leq \mu < \kappa $
, this shows that
$\lambda \leq \mu < \kappa $
, this shows that
![]() $S = \left \lbrace \mu \colon \text {there is a partition of }2^{\omega } \text { into }\mu \text { closed sets} \right \rbrace $
is unbounded below
$S = \left \lbrace \mu \colon \text {there is a partition of }2^{\omega } \text { into }\mu \text { closed sets} \right \rbrace $
is unbounded below
![]() $\kappa $
. By Lemma 2.3,
$\kappa $
. By Lemma 2.3,
![]() $\kappa \in S$
. By Lemma 2.2, this implies every uncountable Polish space can be partitioned into
$\kappa \in S$
. By Lemma 2.2, this implies every uncountable Polish space can be partitioned into
![]() $\kappa $
compact sets.
$\kappa $
compact sets.
Corollary 2.5. For any uncountable Polish space X,
 $$ \begin{align*} \mathfrak{sp}({\small\text{closed}}) &= \left\lbrace \kappa> \aleph_0 \colon \text{there is a partition of } X \text{ into }\kappa \text{ compact sets} \right\rbrace \\ &= \left\lbrace \kappa > \aleph_0 \colon \text{there is a partition of } X \text{ into }\kappa \text{ closed sets} \right\rbrace \\ &= \left\lbrace \kappa > \aleph_0 \colon \text{there is a partition of } X \text{ into }\kappa \ F_{\sigma} \text{ sets} \right\rbrace. \end{align*} $$
$$ \begin{align*} \mathfrak{sp}({\small\text{closed}}) &= \left\lbrace \kappa> \aleph_0 \colon \text{there is a partition of } X \text{ into }\kappa \text{ compact sets} \right\rbrace \\ &= \left\lbrace \kappa > \aleph_0 \colon \text{there is a partition of } X \text{ into }\kappa \text{ closed sets} \right\rbrace \\ &= \left\lbrace \kappa > \aleph_0 \colon \text{there is a partition of } X \text{ into }\kappa \ F_{\sigma} \text{ sets} \right\rbrace. \end{align*} $$
Corollary 2.6.
![]() $\min \!\big ( \mathfrak {sp}({\small\text{closed}}) \big ) = \acute {\mathfrak {n}} \geq {\mathfrak d}$
.
$\min \!\big ( \mathfrak {sp}({\small\text{closed}}) \big ) = \acute {\mathfrak {n}} \geq {\mathfrak d}$
.
We note that the inequality
![]() $\acute {\mathfrak {n}} \geq {\mathfrak d}$
has been observed before, and can be considered folklore. It is (arguably) implicit in [Reference Miller, Barwise, Keisler and Kunen17], and was observed explicitly by Hrušak in [Reference Hrušák13] and later by Banakh in [Reference Banakh1]. Anticipating the main theorem in Section 3, note that this inequality gives us an easy way of excluding an initial segment of the uncountable cardinals from
$\acute {\mathfrak {n}} \geq {\mathfrak d}$
has been observed before, and can be considered folklore. It is (arguably) implicit in [Reference Miller, Barwise, Keisler and Kunen17], and was observed explicitly by Hrušak in [Reference Hrušák13] and later by Banakh in [Reference Banakh1]. Anticipating the main theorem in Section 3, note that this inequality gives us an easy way of excluding an initial segment of the uncountable cardinals from
![]() $\mathfrak {sp}({\small\text{closed}})$
: simply make
$\mathfrak {sp}({\small\text{closed}})$
: simply make
![]() ${\mathfrak d}$
big.
${\mathfrak d}$
big.
Corollary 2.7.
![]() $\mathfrak {sp}({\small\text{closed}})$
is closed under singular limits.
$\mathfrak {sp}({\small\text{closed}})$
is closed under singular limits.
It is worth pointing out that the same result holds for
![]() $\mathfrak {sp}({\small\text{Borel}})$
, by a very similar argument. The analogous result also holds for the set
$\mathfrak {sp}({\small\text{Borel}})$
, by a very similar argument. The analogous result also holds for the set
![]() $\mathfrak {sp}({\scriptstyle\text{MAD}})$
mentioned in the introduction [Reference Hechler11, Theorem 3.1], again by a similar argument.
$\mathfrak {sp}({\scriptstyle\text{MAD}})$
mentioned in the introduction [Reference Hechler11, Theorem 3.1], again by a similar argument.
Theorem 2.8.
![]() $\mathfrak {sp}({\small\text{Borel}})$
is closed under singular limits.
$\mathfrak {sp}({\small\text{Borel}})$
is closed under singular limits.
Proof Suppose
![]() $\kappa $
is a singular cardinal and
$\kappa $
is a singular cardinal and
![]() $\mathfrak {sp}({\small\text{Borel}}) \cap \kappa $
is unbounded in
$\mathfrak {sp}({\small\text{Borel}}) \cap \kappa $
is unbounded in
![]() $\kappa $
. Let
$\kappa $
. Let
![]() $\nu = \mathrm {cf}(\kappa ) < \kappa $
, and let
$\nu = \mathrm {cf}(\kappa ) < \kappa $
, and let
![]() $\left \langle \alpha _{\xi } \colon \xi < \nu \right \rangle $
be a sequence of cardinals in
$\left \langle \alpha _{\xi } \colon \xi < \nu \right \rangle $
be a sequence of cardinals in
![]() $\mathfrak {sp}({\small\text{Borel}})$
increasing up to
$\mathfrak {sp}({\small\text{Borel}})$
increasing up to
![]() $\kappa $
. Fix some
$\kappa $
. Fix some
![]() $\lambda \in \mathfrak {sp}({\small\text{Borel}})$
with
$\lambda \in \mathfrak {sp}({\small\text{Borel}})$
with
![]() $\nu \leq \lambda < \kappa $
.
$\nu \leq \lambda < \kappa $
.
Let
![]() $\left \lbrace B_{\xi } \colon \xi < \lambda \right \rbrace $
be a partition of
$\left \lbrace B_{\xi } \colon \xi < \lambda \right \rbrace $
be a partition of
![]() $2^{\omega }$
into
$2^{\omega }$
into
![]() $\lambda $
Borel sets. Observe that
$\lambda $
Borel sets. Observe that
![]() $\left \lbrace 2^{\omega } \times B_{\xi } \colon \xi < \lambda \right \rbrace $
is a partition of
$\left \lbrace 2^{\omega } \times B_{\xi } \colon \xi < \lambda \right \rbrace $
is a partition of
![]() $2^{\omega } \times 2^{\omega } \approx 2^{\omega }$
into
$2^{\omega } \times 2^{\omega } \approx 2^{\omega }$
into
![]() $\lambda $
uncountable Borel sets. Thus we may (and do) assume that
$\lambda $
uncountable Borel sets. Thus we may (and do) assume that
![]() $B_{\xi }$
is uncountable for each
$B_{\xi }$
is uncountable for each
![]() $\xi < \lambda $
. Every uncountable Borel set contains a closed subspace homeomorphic to
$\xi < \lambda $
. Every uncountable Borel set contains a closed subspace homeomorphic to
![]() $2^{\omega }$
. For each
$2^{\omega }$
. For each
![]() $\xi < \nu $
, fix
$\xi < \nu $
, fix
![]() $C_{\xi } \subseteq B_{\xi }$
with
$C_{\xi } \subseteq B_{\xi }$
with
![]() $C_{\xi } \approx 2^{\omega }$
, and let
$C_{\xi } \approx 2^{\omega }$
, and let
![]() $\mathcal {P}_{\xi }$
be a partition of
$\mathcal {P}_{\xi }$
be a partition of
![]() $C_{\xi }$
into
$C_{\xi }$
into
![]() $\alpha _{\xi }$
Borel sets. Then
$\alpha _{\xi }$
Borel sets. Then
![]() $\bigcup _{\xi < \nu }\mathcal {P}_{\xi } \cup \left \lbrace B_{\xi } \setminus C_{\xi } \colon \xi < \nu \right \rbrace \cup \left \lbrace B_{\xi } \colon \nu \leq \xi < \lambda \right \rbrace $
is a partition of
$\bigcup _{\xi < \nu }\mathcal {P}_{\xi } \cup \left \lbrace B_{\xi } \setminus C_{\xi } \colon \xi < \nu \right \rbrace \cup \left \lbrace B_{\xi } \colon \nu \leq \xi < \lambda \right \rbrace $
is a partition of
![]() $2^{\omega }$
into
$2^{\omega }$
into
![]() $\kappa $
Borel sets.
$\kappa $
Borel sets.
We end this section with some terminology regarding trees, and two open questions regarding the Sierpiński cardinal
![]() $\acute {\mathfrak {n}}$
.
$\acute {\mathfrak {n}}$
.
Recall that a subtree of
![]() $2^{<\omega }$
is a subset of
$2^{<\omega }$
is a subset of
![]() $2^{<\omega }$
that is closed under taking initial segments. A subtree T of
$2^{<\omega }$
that is closed under taking initial segments. A subtree T of
![]() $2^{<\omega }$
is pruned if every node of T has a successor in T. A branch through T means a function
$2^{<\omega }$
is pruned if every node of T has a successor in T. A branch through T means a function
![]() $b \in 2^{\omega }$
such that
$b \in 2^{\omega }$
such that
![]() $b \!\restriction \! n \in T$
for all
$b \!\restriction \! n \in T$
for all
![]() $n < \omega $
. If T is a subtree of
$n < \omega $
. If T is a subtree of
![]() $2^{<\omega }$
, we denote by
$2^{<\omega }$
, we denote by
![]() $[\![T]\!]$
the set of all branches through T. It is not difficult to see that
$[\![T]\!]$
the set of all branches through T. It is not difficult to see that
![]() $[\![T]\!]$
is closed in
$[\![T]\!]$
is closed in
![]() $2^{\omega }$
for any subtree T of
$2^{\omega }$
for any subtree T of
![]() $2^{<\omega }$
; and conversely, for every closed
$2^{<\omega }$
; and conversely, for every closed
![]() $C \subseteq 2^{\omega }$
there is a subtree T of
$C \subseteq 2^{\omega }$
there is a subtree T of
![]() $2^{<\omega }$
with
$2^{<\omega }$
with
![]() $C = [\![T]\!]$
(for details, see [Reference Kechris14, Chapter 2]). Similar terminology is used for subtrees of
$C = [\![T]\!]$
(for details, see [Reference Kechris14, Chapter 2]). Similar terminology is used for subtrees of
![]() $\omega ^{<\omega }$
or of
$\omega ^{<\omega }$
or of
![]() $2^{<k}$
.
$2^{<k}$
.
Representing closed sets with trees in this way, Theorem 2.4 states that
![]() $\kappa \in \mathfrak {sp}({\small\text{closed}})$
if and only if
$\kappa \in \mathfrak {sp}({\small\text{closed}})$
if and only if
![]() $\kappa> \aleph _0$
and there is a MAD family of
$\kappa> \aleph _0$
and there is a MAD family of
![]() $\kappa $
subtrees of
$\kappa $
subtrees of
![]() $2^{<\omega }$
. Similarly,
$2^{<\omega }$
. Similarly,
![]() $\kappa \in \mathfrak {sp}({\small\text{closed}})$
if and only if there is a MAD family of
$\kappa \in \mathfrak {sp}({\small\text{closed}})$
if and only if there is a MAD family of
![]() $\kappa $
finitely branching, pruned subtrees of
$\kappa $
finitely branching, pruned subtrees of
![]() $\omega ^{<\omega }$
. These characterizations of
$\omega ^{<\omega }$
. These characterizations of
![]() $\mathfrak {sp}({\small\text{closed}})$
explain Hrušák’s notation, writing
$\mathfrak {sp}({\small\text{closed}})$
explain Hrušák’s notation, writing
![]() $\mathfrak {a}_T$
for
$\mathfrak {a}_T$
for
![]() $\min \!\big ( \mathfrak {sp}({\small\text{closed}}) \big )$
. This relationship between
$\min \!\big ( \mathfrak {sp}({\small\text{closed}}) \big )$
. This relationship between
![]() $\acute {\mathfrak {n}}$
and
$\acute {\mathfrak {n}}$
and
![]() $\mathfrak {a}$
raises the following questions.
$\mathfrak {a}$
raises the following questions.
Question 2.9. Is it consistent that
![]() $\acute {\mathfrak {n}}$
has countable cofinality?
$\acute {\mathfrak {n}}$
has countable cofinality?
The corresponding question for
![]() $\mathfrak {a}$
was solved by Brendle in [Reference Brendle4], where he used Shelah’s template forcing technique to obtain a model of
$\mathfrak {a}$
was solved by Brendle in [Reference Brendle4], where he used Shelah’s template forcing technique to obtain a model of
![]() $\mathfrak {a} = \aleph _{\omega }$
. It is relatively easy to make
$\mathfrak {a} = \aleph _{\omega }$
. It is relatively easy to make
![]() $\acute {\mathfrak {n}}$
singular of uncountable cofinality: e.g., by adding
$\acute {\mathfrak {n}}$
singular of uncountable cofinality: e.g., by adding
![]() $\aleph _{\omega _1}$
Cohen reals to a model of
$\aleph _{\omega _1}$
Cohen reals to a model of
![]() $\mathsf {CH}$
, we get a model where
$\mathsf {CH}$
, we get a model where
![]() ${\mathfrak d} = \acute {\mathfrak {n}} = \mathfrak {c} = \aleph _{\omega _1}$
.
${\mathfrak d} = \acute {\mathfrak {n}} = \mathfrak {c} = \aleph _{\omega _1}$
.
It is also simple to prove the consistency of
![]() $\mathfrak {a} < \acute {\mathfrak {n}}$
. This holds, for example, in the Cohen model, where
$\mathfrak {a} < \acute {\mathfrak {n}}$
. This holds, for example, in the Cohen model, where
![]() $\aleph _1 = \mathfrak {a} < {\mathfrak d} = \acute {\mathfrak {n}} = \mathfrak {c}$
.
$\aleph _1 = \mathfrak {a} < {\mathfrak d} = \acute {\mathfrak {n}} = \mathfrak {c}$
.
Question 2.10. Is
![]() $\mathfrak {a} \leq \acute {\mathfrak {n}}$
?
$\mathfrak {a} \leq \acute {\mathfrak {n}}$
?
We note that if
![]() $\acute {\mathfrak {n}} < \mathfrak {a}$
is consistent, then proving it is likely very difficult. This is because
$\acute {\mathfrak {n}} < \mathfrak {a}$
is consistent, then proving it is likely very difficult. This is because
![]() $\acute {\mathfrak {n}} < \mathfrak {a}$
implies
$\acute {\mathfrak {n}} < \mathfrak {a}$
implies
![]() ${\mathfrak d} < \mathfrak {a}$
. The consistency of
${\mathfrak d} < \mathfrak {a}$
. The consistency of
![]() ${\mathfrak d} < \mathfrak {a}$
was an open question for a long time, solved by Shelah in [Reference Shelah20]. Shelah’s technique will not work, however, for obtaining a model of
${\mathfrak d} < \mathfrak {a}$
was an open question for a long time, solved by Shelah in [Reference Shelah20]. Shelah’s technique will not work, however, for obtaining a model of
![]() $\acute {\mathfrak {n}} < \mathfrak {a}$
: his technique makes
$\acute {\mathfrak {n}} < \mathfrak {a}$
: his technique makes
![]() $\acute {\mathfrak {n}}$
large for the same reasons it makes
$\acute {\mathfrak {n}}$
large for the same reasons it makes
![]() $\mathfrak {a}$
large. (Roughly, by an “averaging of names” argument, an ultrapower
$\mathfrak {a}$
large. (Roughly, by an “averaging of names” argument, an ultrapower
![]() $\mathbb {P}^{\kappa }/{\mathcal U}$
forces that if
$\mathbb {P}^{\kappa }/{\mathcal U}$
forces that if
![]() $\acute {\mathfrak {n}} \geq \kappa $
then
$\acute {\mathfrak {n}} \geq \kappa $
then
![]() $\acute {\mathfrak {n}} = \mathfrak {c}$
.)
$\acute {\mathfrak {n}} = \mathfrak {c}$
.)
3 Forcing an (almost) arbitrary spectrum
Every
![]() $\kappa \in \mathfrak {sp}({\small\text{Borel}})$
is an example what Blass calls a “
$\kappa \in \mathfrak {sp}({\small\text{Borel}})$
is an example what Blass calls a “
![]() $\mathbf {\Delta }^1_1$
characteristic” in [Reference Blass and Judah2]. Blass proves [Reference Blass and Judah2, Theorems 8 and 9] that there can be many cardinals between
$\mathbf {\Delta }^1_1$
characteristic” in [Reference Blass and Judah2]. Blass proves [Reference Blass and Judah2, Theorems 8 and 9] that there can be many cardinals between
![]() $\aleph _1$
and
$\aleph _1$
and
![]() $\mathfrak {c}$
that are not
$\mathfrak {c}$
that are not
![]() $\mathbf {\Delta }^1_1$
characteristics, and therefore are not in
$\mathbf {\Delta }^1_1$
characteristics, and therefore are not in
![]() $\mathfrak {sp}({\small\text{Borel}})$
. For example, it is consistent to have the set of
$\mathfrak {sp}({\small\text{Borel}})$
. For example, it is consistent to have the set of
![]() $\mathbf {\Delta }^1_1$
characteristics be equal to precisely
$\mathbf {\Delta }^1_1$
characteristics be equal to precisely
![]() $\left \lbrace \aleph _n \colon n \text { is a power of }17 \right \rbrace \cup \{\aleph _{\omega },\aleph _{\omega +1}\}$
. Blass’ method does not guarantee that any of these
$\left \lbrace \aleph _n \colon n \text { is a power of }17 \right \rbrace \cup \{\aleph _{\omega },\aleph _{\omega +1}\}$
. Blass’ method does not guarantee that any of these
![]() $\mathbf {\Delta }^1_1$
characteristics will be in
$\mathbf {\Delta }^1_1$
characteristics will be in
![]() $\mathfrak {sp}({\small\text{Borel}})$
, except of course for
$\mathfrak {sp}({\small\text{Borel}})$
, except of course for
![]() $\aleph _1$
and
$\aleph _1$
and
![]() $\mathfrak {c}$
. But his results do show at least that
$\mathfrak {c}$
. But his results do show at least that
![]() $\mathfrak {sp}({\small\text{Borel}})$
can contain large gaps, and that it is possible to surgically exclude specific cardinals from
$\mathfrak {sp}({\small\text{Borel}})$
can contain large gaps, and that it is possible to surgically exclude specific cardinals from
![]() $\mathfrak {sp}({\small\text{Borel}})$
. (We should mention that the consistency of having
$\mathfrak {sp}({\small\text{Borel}})$
. (We should mention that the consistency of having
![]() $\aleph _2 \notin \mathfrak {sp}({\small\text{Borel}})$
predates Blass’ work, and is due to Miller [Reference Miller18].)
$\aleph _2 \notin \mathfrak {sp}({\small\text{Borel}})$
predates Blass’ work, and is due to Miller [Reference Miller18].)
In the other direction, extending a prior result of Miller’s [Reference Miller, Barwise, Keisler and Kunen17, Theorem 4], Miller and the author showed in [Reference Brian and Miller5, Theorem 3.12] that:
Theorem 3.1. For any
![]() $\kappa \geq \mathfrak {c}$
with
$\kappa \geq \mathfrak {c}$
with
![]() $\mathrm {cf}(\kappa )> \omega $
, there is a ccc forcing extension in which
$\mathrm {cf}(\kappa )> \omega $
, there is a ccc forcing extension in which
![]() $\mathfrak {c} = \kappa $
and
$\mathfrak {c} = \kappa $
and
![]() $\mathfrak {sp}({\small\text{closed}}) = [\aleph _1,\kappa ]$
.
$\mathfrak {sp}({\small\text{closed}}) = [\aleph _1,\kappa ]$
.
In particular, for any set C of cardinals, there is a ccc forcing extension in which
![]() $C \subseteq \mathfrak {sp}({\small\text{closed}})$
. We now sketch a proof of this theorem, in order to introduce some of the ideas used in the proof of the main theorem below, but in a simpler context. This sketch can be skipped by the reader requiring no such introduction.
$C \subseteq \mathfrak {sp}({\small\text{closed}})$
. We now sketch a proof of this theorem, in order to introduce some of the ideas used in the proof of the main theorem below, but in a simpler context. This sketch can be skipped by the reader requiring no such introduction.
Proof sketch of Theorem 3.1
Given some
![]() $X \subseteq 2^{\omega }$
with empty interior, let
$X \subseteq 2^{\omega }$
with empty interior, let
![]() $\mathbb {T}_{\!X}$
be the poset whose conditions are pairs
$\mathbb {T}_{\!X}$
be the poset whose conditions are pairs
![]() $(t,B)$
, where
$(t,B)$
, where
-
∘ There is some
 $k \in \omega $
such that t is a subtree of
$k \in \omega $
such that t is a subtree of
 $2^{<k}$
, and t is pruned: i.e., if
$2^{<k}$
, and t is pruned: i.e., if
 $\sigma \in t$
with
$\sigma \in t$
with
 $|\sigma | < k$
, then
$|\sigma | < k$
, then
 $\sigma $
has a proper extension in t.
$\sigma $
has a proper extension in t. -
∘ B is a finite subset of
 $2^{\omega } \setminus X$
, and
$2^{\omega } \setminus X$
, and
 $b \!\restriction \! k$
is a branch of t for each
$b \!\restriction \! k$
is a branch of t for each
 $b \in B$
.
$b \in B$
.
The ordering on
![]() $\mathbb {T}_{\!X}$
is defined by:
$\mathbb {T}_{\!X}$
is defined by:
![]() $(t',B')$
extends
$(t',B')$
extends
![]() $(t,B)$
if and only if
$(t,B)$
if and only if
![]() $B' \supseteq B$
and
$B' \supseteq B$
and
![]() $t'$
is an end extension of t (meaning that
$t'$
is an end extension of t (meaning that
![]() $t = t' \cap 2^{<k}$
for some k).
$t = t' \cap 2^{<k}$
for some k).
Roughly, a condition
![]() $(t,B)$
can be thought of as a finite approximation t to a subtree T of
$(t,B)$
can be thought of as a finite approximation t to a subtree T of
![]() $2^{<\omega }$
that we are trying to build generically, and a promise that some finite set B of reals will be branches of T.
$2^{<\omega }$
that we are trying to build generically, and a promise that some finite set B of reals will be branches of T.
For any
![]() $X \subseteq 2^{\omega }$
,
$X \subseteq 2^{\omega }$
,
![]() $\mathbb {T}_{\!X}$
is
$\mathbb {T}_{\!X}$
is
![]() $\sigma $
-centered. The poset
$\sigma $
-centered. The poset
![]() $\mathbb {T}_{\!X}$
generically adds an infinite pruned subtree T of
$\mathbb {T}_{\!X}$
generically adds an infinite pruned subtree T of
![]() $2^{<\omega }$
, defined from a generic filter G on
$2^{<\omega }$
, defined from a generic filter G on
![]() $\mathbb {T}_{\!X}$
as
$\mathbb {T}_{\!X}$
as
![]() $T = \bigcup \left \lbrace t \colon (t,B) \in G \text { for some } B \right \rbrace $
. (Equivalently, T is the evaluation in
$T = \bigcup \left \lbrace t \colon (t,B) \in G \text { for some } B \right \rbrace $
. (Equivalently, T is the evaluation in
![]() $V[G]$
of the name
$V[G]$
of the name
![]() $\dot T = \left \lbrace \langle \sigma ,q \rangle \colon q = (t,B) \text { for some } B \text {, and } \sigma \in t \right \rbrace .$
) In the extension,
$\dot T = \left \lbrace \langle \sigma ,q \rangle \colon q = (t,B) \text { for some } B \text {, and } \sigma \in t \right \rbrace .$
) In the extension,
![]() $[\![T]\!]$
is a closed subset of
$[\![T]\!]$
is a closed subset of
![]() $2^{\omega }$
disjoint from X.
$2^{\omega }$
disjoint from X.
Let
![]() $\mathbb {T}_{\!X}^{\,\omega }$
denote the finite support product of countably many copies of
$\mathbb {T}_{\!X}^{\,\omega }$
denote the finite support product of countably many copies of
![]() $\mathbb {T}_{\!X}$
. For any
$\mathbb {T}_{\!X}$
. For any
![]() $X \subseteq 2^{\omega }$
,
$X \subseteq 2^{\omega }$
,
![]() $\mathbb {T}_{\!X}^{\,\omega }$
is
$\mathbb {T}_{\!X}^{\,\omega }$
is
![]() $\sigma $
-centered. The poset
$\sigma $
-centered. The poset
![]() $\mathbb {T}_{\!X}^{\,\omega }$
generically adds countably many infinite pruned subtrees
$\mathbb {T}_{\!X}^{\,\omega }$
generically adds countably many infinite pruned subtrees
![]() $T_0,T_1,T_2,\dots $
of
$T_0,T_1,T_2,\dots $
of
![]() $2^{<\omega }$
, and in the extension,
$2^{<\omega }$
, and in the extension,
In other words,
![]() $\mathbb {T}_{\!X}^{\,\omega }$
generically adds an
$\mathbb {T}_{\!X}^{\,\omega }$
generically adds an
![]() $F_{\sigma }$
subset of
$F_{\sigma }$
subset of
![]() $2^{\omega }$
that intersects the ground model reals in precisely the complement of X. (Note: this poset may look familiar: it is the one usually used for showing that
$2^{\omega }$
that intersects the ground model reals in precisely the complement of X. (Note: this poset may look familiar: it is the one usually used for showing that
![]() $\mathsf {M}$
artin’s
$\mathsf {M}$
artin’s
![]() $\mathsf {A}$
xiom implies every
$\mathsf {A}$
xiom implies every
![]() $<\!\mathfrak {c}$
-sized subset of
$<\!\mathfrak {c}$
-sized subset of
![]() $2^{\omega }$
is a Q-set.)
$2^{\omega }$
is a Q-set.)
Let C denote the set of cardinals in
![]() $[\aleph _1,\kappa ]$
. We now define a finite support iteration of length
$[\aleph _1,\kappa ]$
. We now define a finite support iteration of length
![]() $\omega _1$
as follows. At stage
$\omega _1$
as follows. At stage
![]() $0$
, force with the poset
$0$
, force with the poset
![]() $\mathbb {Q}_0 = \mathbb {C}_{\kappa }$
of finite partial functions
$\mathbb {Q}_0 = \mathbb {C}_{\kappa }$
of finite partial functions
![]() $\kappa \to 2$
, in order to add a set of
$\kappa \to 2$
, in order to add a set of
![]() $\kappa $
mutually generic Cohen reals. Let
$\kappa $
mutually generic Cohen reals. Let
![]() $\left \lbrace c_{\xi } \colon \xi < \kappa \right \rbrace $
be an enumeration of these Cohen reals in
$\left \lbrace c_{\xi } \colon \xi < \kappa \right \rbrace $
be an enumeration of these Cohen reals in
![]() $V^{\mathbb {Q}_0}$
, and for each
$V^{\mathbb {Q}_0}$
, and for each
![]() $\mu \in C$
, let
$\mu \in C$
, let
![]() $\mathcal {P}_0^{\mu } = \left \lbrace \{c_{\xi }\} \colon \xi < \mu \right \rbrace $
. Note that
$\mathcal {P}_0^{\mu } = \left \lbrace \{c_{\xi }\} \colon \xi < \mu \right \rbrace $
. Note that
![]() $\mathcal {P}^{\mu }_0$
is a
$\mathcal {P}^{\mu }_0$
is a
![]() $\mu $
-sized collection of disjoint subsets of
$\mu $
-sized collection of disjoint subsets of
![]() $\mathbb {R}$
: we think of
$\mathbb {R}$
: we think of
![]() $\mathcal {P}^{\mu }_0$
as a first approximation to a
$\mathcal {P}^{\mu }_0$
as a first approximation to a
![]() $\mu $
-sized partition we are trying to build. At a later stage
$\mu $
-sized partition we are trying to build. At a later stage
![]() $\alpha $
of the iteration, suppose we have already obtained, for each
$\alpha $
of the iteration, suppose we have already obtained, for each
![]() $\mu \in C$
, a
$\mu \in C$
, a
![]() $\mu $
-sized collection
$\mu $
-sized collection
![]() $\mathcal {P}^{\mu }_{\alpha }$
of disjoint subsets of
$\mathcal {P}^{\mu }_{\alpha }$
of disjoint subsets of
![]() $\mathbb {R}$
. In
$\mathbb {R}$
. In
![]() $V^{\mathbb {Q}_{\alpha }}$
, define
$V^{\mathbb {Q}_{\alpha }}$
, define
![]() $X^{\mu }_{\alpha } = \bigcup \mathcal {P}^{\mu }_{\alpha }$
for each
$X^{\mu }_{\alpha } = \bigcup \mathcal {P}^{\mu }_{\alpha }$
for each
![]() $\mu \in C$
, and then obtain
$\mu \in C$
, and then obtain
![]() $V^{\mathbb {Q}_{\alpha +1}}$
from
$V^{\mathbb {Q}_{\alpha +1}}$
from
![]() $V^{\mathbb {Q}_{\alpha }}$
by forcing with
$V^{\mathbb {Q}_{\alpha }}$
by forcing with
![]() $\prod _{\mu \in C}\mathbb {T}^{\,\omega }_{\!X_{\alpha }^{\mu }}$
. This adds countably many generic trees
$\prod _{\mu \in C}\mathbb {T}^{\,\omega }_{\!X_{\alpha }^{\mu }}$
. This adds countably many generic trees
![]() $T^{\mu }_{\alpha ,0},T^{\mu }_{\alpha ,1},T^{\mu }_{\alpha ,2},\dots $
for each
$T^{\mu }_{\alpha ,0},T^{\mu }_{\alpha ,1},T^{\mu }_{\alpha ,2},\dots $
for each
![]() $\mu \in C$
, and in
$\mu \in C$
, and in
![]() $V^{\mathbb {Q}_{\alpha +1}}$
we define
$V^{\mathbb {Q}_{\alpha +1}}$
we define
![]() $\mathcal {P}^{\mu }_{\alpha +1} = \mathcal {P}^{\mu }_{\alpha } \cup \{ \bigcup _{n \in \omega } [\![T^{\mu }_{\alpha ,n}]\!] \}$
.
$\mathcal {P}^{\mu }_{\alpha +1} = \mathcal {P}^{\mu }_{\alpha } \cup \{ \bigcup _{n \in \omega } [\![T^{\mu }_{\alpha ,n}]\!] \}$
.
At the end of the iteration, in
![]() $V^{\mathbb {Q}_{\omega _1}}$
, let
$V^{\mathbb {Q}_{\omega _1}}$
, let
![]() $\mathcal {P}^{\mu } = \bigcup _{\alpha < \omega _1}\mathcal {P}_{\alpha }^{\mu }$
. This is a
$\mathcal {P}^{\mu } = \bigcup _{\alpha < \omega _1}\mathcal {P}_{\alpha }^{\mu }$
. This is a
![]() $\mu $
-sized collection of disjoint
$\mu $
-sized collection of disjoint
![]() $F_{\sigma }$
subsets of
$F_{\sigma }$
subsets of
![]() $\mathbb {R}$
. Furthermore, if x is a real in
$\mathbb {R}$
. Furthermore, if x is a real in
![]() $V^{\mathbb {Q}_{\omega _1}}$
, then there is some
$V^{\mathbb {Q}_{\omega _1}}$
, then there is some
![]() $\alpha < \omega _1$
with
$\alpha < \omega _1$
with
![]() $x \in V^{\mathbb {Q}_{\alpha }}$
. At that stage of the iteration, either
$x \in V^{\mathbb {Q}_{\alpha }}$
. At that stage of the iteration, either
![]() $x \in \bigcup \mathcal {P}^{\mu }_{\alpha }$
, or if not, then
$x \in \bigcup \mathcal {P}^{\mu }_{\alpha }$
, or if not, then
![]() $x \in \bigcup _{n \in \omega } [\![T^{\alpha }_{\mu ,n}]\!]$
because
$x \in \bigcup _{n \in \omega } [\![T^{\alpha }_{\mu ,n}]\!]$
because
![]() $\textstyle (2^{\omega })^{V^{\mathbb {P}_{\alpha }}} \cap \bigcup _{n < \omega }[\![T^{\alpha }_{\mu ,n}]\!] \,=\, (2^{\omega })^{V^{\mathbb {P}_{\alpha }}} \setminus X_{\alpha }^{\mu }$
. Either way,
$\textstyle (2^{\omega })^{V^{\mathbb {P}_{\alpha }}} \cap \bigcup _{n < \omega }[\![T^{\alpha }_{\mu ,n}]\!] \,=\, (2^{\omega })^{V^{\mathbb {P}_{\alpha }}} \setminus X_{\alpha }^{\mu }$
. Either way,
![]() $x \in \bigcup \mathcal {P}^{\mu }_{\alpha +1} \subseteq \bigcup \mathcal {P}^{\mu }$
. Thus
$x \in \bigcup \mathcal {P}^{\mu }_{\alpha +1} \subseteq \bigcup \mathcal {P}^{\mu }$
. Thus
![]() $\mathcal {P}^{\mu }$
is a partition of
$\mathcal {P}^{\mu }$
is a partition of
![]() $2^{\omega }$
into
$2^{\omega }$
into
![]() $F_{\sigma }$
sets in
$F_{\sigma }$
sets in
![]() $V^{\mathbb {Q}_{\omega _1}}$
, and this means
$V^{\mathbb {Q}_{\omega _1}}$
, and this means
![]() $\mu \in \mathfrak {sp}({\small\text{closed}})$
by Corollary 2.5.
$\mu \in \mathfrak {sp}({\small\text{closed}})$
by Corollary 2.5.
The main theorem is proved with a modification of this poset, with two major changes. First, the set C will not necessarily be an interval of cardinals, but will consist only of those cardinals we wish to add to
![]() $\mathfrak {sp}({\small\text{closed}})$
. Second, instead of a true iteration, we use a streamlined modification. This modified iteration has actual finite sequences (rather than names for them) for the working parts of the
$\mathfrak {sp}({\small\text{closed}})$
. Second, instead of a true iteration, we use a streamlined modification. This modified iteration has actual finite sequences (rather than names for them) for the working parts of the
![]() $\mathbb {T}_{\!X_{\alpha }^{\mu }}$
, which is helpful for proving that certain permutations of the Cohen reals extend to automorphisms of the entire poset. (And these automorphisms are essential for excluding cardinals
$\mathbb {T}_{\!X_{\alpha }^{\mu }}$
, which is helpful for proving that certain permutations of the Cohen reals extend to automorphisms of the entire poset. (And these automorphisms are essential for excluding cardinals
![]() $\notin \!C$
from
$\notin \!C$
from
![]() $\mathfrak {sp}({\small\text{Borel}})$
.) The definition of this modified iteration is reminiscent of the template forcing notions in [Reference Brendle3], but with a well-ordered template, so that it is essentially an iteration.
$\mathfrak {sp}({\small\text{Borel}})$
.) The definition of this modified iteration is reminiscent of the template forcing notions in [Reference Brendle3], but with a well-ordered template, so that it is essentially an iteration.
Theorem 3.2. Let C be a set of uncountable cardinals such that:
-
∘
 $\min (C)$
is regular,
$\min (C)$
is regular, -
∘
 $|C| < \min (C)$
,
$|C| < \min (C)$
, -
∘ C has a maximum with
 $\mathrm {cf}(\max (C))> \omega $
,
$\mathrm {cf}(\max (C))> \omega $
, -
∘ C is closed under singular limits, and
-
∘ if
 $\lambda $
is singular and
$\lambda $
is singular and
 $\lambda \in C$
, then
$\lambda \in C$
, then
 $\lambda ^+ \in C$
.
$\lambda ^+ \in C$
.
Assuming
![]() $\mathsf {GCH}$
holds up to
$\mathsf {GCH}$
holds up to
![]() $\max (C)$
, there is a ccc forcing extension in which
$\max (C)$
, there is a ccc forcing extension in which
![]() $\mathfrak {c} = \max (C)$
,
$\mathfrak {c} = \max (C)$
,
![]() $\mathfrak {sp}({\small\text{closed}}) = C$
, and if
$\mathfrak {sp}({\small\text{closed}}) = C$
, and if
![]() $\min (C) < \lambda \notin C$
then
$\min (C) < \lambda \notin C$
then
![]() $\lambda \notin \mathfrak {sp}({\small\text{Borel}})$
.
$\lambda \notin \mathfrak {sp}({\small\text{Borel}})$
.
Before proving this theorem, let us deduce some relatively easy corollaries from it, including the results mentioned in the introduction.
Corollary 3.3. Let C be a set of uncountable cardinals such that:
-
∘
 $\aleph _1 \in C$
,
$\aleph _1 \in C$
, -
∘ C is at most countable,
-
∘ C has a maximum with
 $\mathrm {cf}(\max (C))> \omega $
,
$\mathrm {cf}(\max (C))> \omega $
, -
∘ C is closed under singular limits, and
-
∘ if
 $\lambda $
is singular and
$\lambda $
is singular and
 $\lambda \in C$
, then
$\lambda \in C$
, then
 $\lambda ^+ \in C$
.
$\lambda ^+ \in C$
.
Assuming
![]() $\mathsf {GCH}$
holds up to
$\mathsf {GCH}$
holds up to
![]() $\max (C)$
, there is a ccc forcing extension in which
$\max (C)$
, there is a ccc forcing extension in which
![]() $\mathfrak {c} = \max (C)$
and
$\mathfrak {c} = \max (C)$
and
![]() $\mathfrak {sp}({\small\text{Borel}}) = \mathfrak {sp}({\small\text{closed}}) = C$
.
$\mathfrak {sp}({\small\text{Borel}}) = \mathfrak {sp}({\small\text{closed}}) = C$
.
Proof This follows immediately from the previous theorem.
Corollary 3.4. Given any
![]() $A \subseteq \omega \setminus \{0\}$
, there is a forcing extension in which
$A \subseteq \omega \setminus \{0\}$
, there is a forcing extension in which
![]() $\mathfrak {sp}({\small\text{Borel}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _1,\aleph _{\omega },\aleph _{\omega +1}\}$
, and if
$\mathfrak {sp}({\small\text{Borel}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _1,\aleph _{\omega },\aleph _{\omega +1}\}$
, and if
![]() $A \neq \emptyset $
there is a forcing extension in which
$A \neq \emptyset $
there is a forcing extension in which
![]() $\mathfrak {sp}({\small\text{closed}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _{\omega },\aleph _{\omega +1}\}$
.
$\mathfrak {sp}({\small\text{closed}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _{\omega },\aleph _{\omega +1}\}$
.
Proof Fix some
![]() $A \subseteq \omega \setminus \{0\}$
. First pass to a forcing extension in which
$A \subseteq \omega \setminus \{0\}$
. First pass to a forcing extension in which
![]() $\mathsf {GCH}$
holds up to
$\mathsf {GCH}$
holds up to
![]() $\aleph _{\omega +1}$
. Then, for the result about
$\aleph _{\omega +1}$
. Then, for the result about
![]() $\mathfrak {sp}({\small\text{closed}})$
, apply Theorem 3.2 with
$\mathfrak {sp}({\small\text{closed}})$
, apply Theorem 3.2 with
![]() $C = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _{\omega },\aleph _{\omega +1}\}$
. Or, for the result about
$C = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _{\omega },\aleph _{\omega +1}\}$
. Or, for the result about
![]() $\mathfrak {sp}({\small\text{Borel}})$
, apply Corollary 3.3 with
$\mathfrak {sp}({\small\text{Borel}})$
, apply Corollary 3.3 with
![]() $C = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _1,\aleph _{\omega },\aleph _{\omega +1}\}$
.
$C = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _1,\aleph _{\omega },\aleph _{\omega +1}\}$
.
Corollary 3.5. Given any finite nonempty
![]() $A \subseteq \omega \setminus \{0\}$
, there is a forcing extension in which
$A \subseteq \omega \setminus \{0\}$
, there is a forcing extension in which
![]() $\mathfrak {sp}({\small\text{Borel}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _1\}$
, and there is a forcing extension in which
$\mathfrak {sp}({\small\text{Borel}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace \cup \{\aleph _1\}$
, and there is a forcing extension in which
![]() $\mathfrak {sp}({\small\text{closed}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace $
.
$\mathfrak {sp}({\small\text{closed}}) = \left \lbrace \aleph _n \colon n \in A \right \rbrace $
.
Proof This is proved in exactly the same way as the previous corollary, but without
![]() $\aleph _{\omega }$
and
$\aleph _{\omega }$
and
![]() $\aleph _{\omega +1}$
put into C.
$\aleph _{\omega +1}$
put into C.
Proof of Theorem 3.2
Let C be a set of uncountable cardinals satisfying the hypotheses listed in the statement of the theorem, and assume
![]() $\mathsf {GCH}$
holds up to
$\mathsf {GCH}$
holds up to
![]() $\max (C)$
. Let
$\max (C)$
. Let
![]() $\kappa = \min (C)$
and let
$\kappa = \min (C)$
and let
![]() $\theta = \max (C)$
.
$\theta = \max (C)$
.
For each
![]() $\mu \in C$
, let
$\mu \in C$
, let
![]() $I_{\mu } = \mu \times \{\mu ,\theta ^{+}\}$
. (These are merely indexing sets, and for all practical purposes one may think of each
$I_{\mu } = \mu \times \{\mu ,\theta ^{+}\}$
. (These are merely indexing sets, and for all practical purposes one may think of each
![]() $I_{\mu }$
as a set of atoms, or urelements, in the set-theoretic universe. The relevant properties of these
$I_{\mu }$
as a set of atoms, or urelements, in the set-theoretic universe. The relevant properties of these
![]() $I_{\mu }$
’s are that they are pairwise disjoint, each
$I_{\mu }$
’s are that they are pairwise disjoint, each
![]() $I_{\mu }$
has size
$I_{\mu }$
has size
![]() $\mu $
, and the
$\mu $
, and the
![]() $I_{\mu }$
do not “interact” in any accidental way with any other sets in the proof.)
$I_{\mu }$
do not “interact” in any accidental way with any other sets in the proof.)
Let
![]() $I = \bigcup _{\mu \in C}I_{\mu }$
, and let
$I = \bigcup _{\mu \in C}I_{\mu }$
, and let
![]() $\mathbb {P}_0$
denote the poset of finite partial functions from
$\mathbb {P}_0$
denote the poset of finite partial functions from
![]() $I \times \omega $
to
$I \times \omega $
to
![]() $2$
. Note that this is equivalent to the standard poset
$2$
. Note that this is equivalent to the standard poset
![]() $\mathbb {C}_{\theta }$
for adding
$\mathbb {C}_{\theta }$
for adding
![]() $\theta $
mutually generic Cohen reals. For each
$\theta $
mutually generic Cohen reals. For each
![]() $i \in I$
, let
$i \in I$
, let
![]() $c_i$
denote in
$c_i$
denote in
![]() $V^{\mathbb {P}_0}$
the Cohen real added by
$V^{\mathbb {P}_0}$
the Cohen real added by
![]() $\mathbb {P}_0$
in coordinate i. More formally,
$\mathbb {P}_0$
in coordinate i. More formally,
![]() $c_i$
denotes in
$c_i$
denotes in
![]() $V^{\mathbb {P}_0}$
the evaluation of the name
$V^{\mathbb {P}_0}$
the evaluation of the name
![]() $\dot c_i = \left \lbrace \langle (n,j),p\rangle \colon p(i,n) = j \right \rbrace .$
$\dot c_i = \left \lbrace \langle (n,j),p\rangle \colon p(i,n) = j \right \rbrace .$
Next we define, recursively, a poset
![]() $\langle \mathbb {P}_{\alpha },\leq _{\mathbb {P}_{\alpha }} \rangle $
for each
$\langle \mathbb {P}_{\alpha },\leq _{\mathbb {P}_{\alpha }} \rangle $
for each
![]() $\alpha \leq \kappa $
with
$\alpha \leq \kappa $
with
![]() $\alpha> 0$
. At every stage of the recursion,
$\alpha> 0$
. At every stage of the recursion,
![]() $\mathbb {P}_{\alpha }$
is defined so that
$\mathbb {P}_{\alpha }$
is defined so that
![]() $\mathbb {P}_{\beta }$
is a sub-poset of
$\mathbb {P}_{\beta }$
is a sub-poset of
![]() $\mathbb {P}_{\alpha }$
for each
$\mathbb {P}_{\alpha }$
for each
![]() $\beta < \alpha $
. Conditions in
$\beta < \alpha $
. Conditions in
![]() $\mathbb {P}_{\alpha }$
are finite partial functions on
$\mathbb {P}_{\alpha }$
are finite partial functions on
![]() $(I \times \omega ) \cup (\alpha \times C \times \omega )$
, and the
$(I \times \omega ) \cup (\alpha \times C \times \omega )$
, and the
![]() $\mathbb {P}_{\alpha }$
are defined so that for any
$\mathbb {P}_{\alpha }$
are defined so that for any
![]() $\beta < \alpha $
, the restriction of a condition in
$\beta < \alpha $
, the restriction of a condition in
![]() $\mathbb {P}_{\alpha }$
to
$\mathbb {P}_{\alpha }$
to
![]() $(I \times \omega ) \cup (\beta \times C \times \omega )$
is a condition in
$(I \times \omega ) \cup (\beta \times C \times \omega )$
is a condition in
![]() $\mathbb {P}_{\beta }$
.
$\mathbb {P}_{\beta }$
.
At limit stages, we take
![]() $\mathbb {P}_{\alpha } = \bigcup _{\xi < \alpha }\mathbb {P}_{\xi }$
and
$\mathbb {P}_{\alpha } = \bigcup _{\xi < \alpha }\mathbb {P}_{\xi }$
and
![]() $\leq _{\mathbb {P}_{\alpha }} = \bigcup _{\xi < \alpha }\leq _{\mathbb {P}_{\xi }}$
. In other words,
$\leq _{\mathbb {P}_{\alpha }} = \bigcup _{\xi < \alpha }\leq _{\mathbb {P}_{\xi }}$
. In other words,
![]() $\langle \mathbb {P}_{\alpha },\leq _{\mathbb {P}_{\alpha }} \rangle $
is the direct limit of
$\langle \mathbb {P}_{\alpha },\leq _{\mathbb {P}_{\alpha }} \rangle $
is the direct limit of
![]() $\left \langle \langle \mathbb {P}_{\xi },\leq _{\mathbb {P}_{\xi }} \rangle \colon \xi < \alpha \right \rangle $
for limit
$\left \langle \langle \mathbb {P}_{\xi },\leq _{\mathbb {P}_{\xi }} \rangle \colon \xi < \alpha \right \rangle $
for limit
![]() $\alpha $
.
$\alpha $
.
At successor stages, suppose
![]() $\mathbb {P}_{\xi }$
is given for every
$\mathbb {P}_{\xi }$
is given for every
![]() $\xi \leq \beta $
, and
$\xi \leq \beta $
, and
![]() $\mathbb {P}_{\xi } \supseteq \mathbb {P}_{\zeta }$
whenever
$\mathbb {P}_{\xi } \supseteq \mathbb {P}_{\zeta }$
whenever
![]() $\zeta \leq \xi \leq \beta $
. Let
$\zeta \leq \xi \leq \beta $
. Let
![]() $\alpha = \beta +1$
. Conditions in
$\alpha = \beta +1$
. Conditions in
![]() $\mathbb {P}_{\alpha }$
are finite partial functions p on
$\mathbb {P}_{\alpha }$
are finite partial functions p on
![]() $(I \times \omega ) \cup (\alpha \times C \times \omega )$
such that:
$(I \times \omega ) \cup (\alpha \times C \times \omega )$
such that:
-
∘ If
 $(i,n) \in (I \times \omega ) \cap \mathrm {dom}(p)$
, then
$(i,n) \in (I \times \omega ) \cap \mathrm {dom}(p)$
, then
 $p(i,n) \in \{0,1\}$
.
$p(i,n) \in \{0,1\}$
. -
∘ If
 $(\gamma ,\mu ,n) \in \mathrm {dom}(p)$
for some
$(\gamma ,\mu ,n) \in \mathrm {dom}(p)$
for some
 $\gamma \leq \beta $
,
$\gamma \leq \beta $
,
 $\mu \in C$
, and
$\mu \in C$
, and
 $n \in \omega $
, then
$n \in \omega $
, then
 $p(\gamma ,\mu ,n) = (t,B)$
, where:
$p(\gamma ,\mu ,n) = (t,B)$
, where:-
∘ t is a pruned subtree of
 $2^{<k}$
for some
$2^{<k}$
for some
 $k \in \omega $
(in this context, “pruned” means that if
$k \in \omega $
(in this context, “pruned” means that if
 $\sigma \in t$
and
$\sigma \in t$
and
 $|\sigma | < k$
, then
$|\sigma | < k$
, then
 $\sigma $
has an extension in t).
$\sigma $
has an extension in t). -
∘ B is a finite set of nice
 $\mathbb {P}_{\gamma }$
-names for members of
$\mathbb {P}_{\gamma }$
-names for members of
 $2^{\omega }$
such that for every
$2^{\omega }$
such that for every
 $\dot b \in B$
,
$\dot b \in B$
,  $$ \begin{align*} \quad \quad \quad \quad \quad p \!\restriction\! ((I \times \omega) \cup (\gamma \times C \times \omega)) \ \Vdash_{\mathbb{P}_{\gamma}} \quad & \dot b \!\restriction\! j \in t \text{ for every } j < k, \\ & \dot b \neq \dot c_i \text{ for every } i \in I_{\mu}, \text{ and} \\ & \dot b \text{ is not a branch of } \dot T^{\xi}_{\mu,m} \\ & \quad \text{ for any } \xi < \gamma \text{ and } m \in \omega, \end{align*} $$
$$ \begin{align*} \quad \quad \quad \quad \quad p \!\restriction\! ((I \times \omega) \cup (\gamma \times C \times \omega)) \ \Vdash_{\mathbb{P}_{\gamma}} \quad & \dot b \!\restriction\! j \in t \text{ for every } j < k, \\ & \dot b \neq \dot c_i \text{ for every } i \in I_{\mu}, \text{ and} \\ & \dot b \text{ is not a branch of } \dot T^{\xi}_{\mu,m} \\ & \quad \text{ for any } \xi < \gamma \text{ and } m \in \omega, \end{align*} $$
where
 $\dot c_i$
is the
$\dot c_i$
is the
 $\mathbb {P}_0$
-name described above, but interpreted as a
$\mathbb {P}_0$
-name described above, but interpreted as a
 $\mathbb {P}_{\gamma }$
-name, and where for every
$\mathbb {P}_{\gamma }$
-name, and where for every
 $\xi < \gamma $
and
$\xi < \gamma $
and
 $m \in \omega $
,
$m \in \omega $
,
 $\dot T^{\xi }_{\mu ,m}$
is the
$\dot T^{\xi }_{\mu ,m}$
is the
 $\mathbb {P}_{\gamma }$
-name for a subtree of
$\mathbb {P}_{\gamma }$
-name for a subtree of
 $2^{<\omega }$
defined as follows:
$2^{<\omega }$
defined as follows:  $$ \begin{align*}\quad \quad \quad \quad \ \ \dot T^{\xi}_{\mu,m} = \left\lbrace \langle \sigma,q \rangle \colon q(\xi,\mu,m) = (t',B') \text{ for some } B' \text{, and } \sigma \in t' \right\rbrace.\end{align*} $$
$$ \begin{align*}\quad \quad \quad \quad \ \ \dot T^{\xi}_{\mu,m} = \left\lbrace \langle \sigma,q \rangle \colon q(\xi,\mu,m) = (t',B') \text{ for some } B' \text{, and } \sigma \in t' \right\rbrace.\end{align*} $$
-
The extension relation
![]() $\leq _{\mathbb {P}_{\alpha }}$
on
$\leq _{\mathbb {P}_{\alpha }}$
on
![]() $\mathbb {P}_{\alpha }$
is defined as follows: given
$\mathbb {P}_{\alpha }$
is defined as follows: given
![]() $p,q \in \mathbb {P}_{\alpha }$
, we write
$p,q \in \mathbb {P}_{\alpha }$
, we write
![]() $q \leq _{\mathbb {P}_{\alpha }} p$
(meaning that q extends p) if and only if:
$q \leq _{\mathbb {P}_{\alpha }} p$
(meaning that q extends p) if and only if:
-
∘
 $\mathrm {dom}(q) \supseteq \mathrm {dom}(p)$
,
$\mathrm {dom}(q) \supseteq \mathrm {dom}(p)$
, -
∘
 $q \!\restriction \! (I \times \omega ) \supseteq p \!\restriction \! (I \times \omega )$
, and
$q \!\restriction \! (I \times \omega ) \supseteq p \!\restriction \! (I \times \omega )$
, and -
∘ if
 $(\gamma ,\mu ,n) \in \mathrm {dom}(p)$
for some
$(\gamma ,\mu ,n) \in \mathrm {dom}(p)$
for some
 $\gamma \leq \beta $
,
$\gamma \leq \beta $
,
 $\mu \in C$
, and
$\mu \in C$
, and
 $n \in \omega $
, and if
$n \in \omega $
, and if
 $p(\gamma ,\mu ,n) = (t,B)$
and
$p(\gamma ,\mu ,n) = (t,B)$
and
 $q(\gamma ,\mu ,n) = (t',B')$
, then
$q(\gamma ,\mu ,n) = (t',B')$
, then
 $B' \supseteq B$
and
$B' \supseteq B$
and
 $t'$
is an end extension of t (meaning that
$t'$
is an end extension of t (meaning that
 $t = t' \cap 2^{<k}$
for some k).
$t = t' \cap 2^{<k}$
for some k).
Naturally, we abbreviate “
![]() $\leq _{\mathbb {P}_{\alpha }}$
” with “
$\leq _{\mathbb {P}_{\alpha }}$
” with “
![]() $\leq $
” in situations where this creates no ambiguity. We also write
$\leq $
” in situations where this creates no ambiguity. We also write
![]() $p \!\restriction \! \alpha $
as an abbreviation for
$p \!\restriction \! \alpha $
as an abbreviation for
![]() $p \!\restriction \! ((I \times \omega ) \cup (\alpha \times C \times \omega ))$
where doing so creates no ambiguity.
$p \!\restriction \! ((I \times \omega ) \cup (\alpha \times C \times \omega ))$
where doing so creates no ambiguity.
This completes the recursive definition of the
![]() $\mathbb {P}_{\alpha }$
and
$\mathbb {P}_{\alpha }$
and
![]() $\leq _{\mathbb {P}_{\alpha }}$
. It is easy to see that
$\leq _{\mathbb {P}_{\alpha }}$
. It is easy to see that
![]() $\leq _{\mathbb {P}_{\alpha }}$
is a partial order on
$\leq _{\mathbb {P}_{\alpha }}$
is a partial order on
![]() $\mathbb {P}_{\alpha }$
for all
$\mathbb {P}_{\alpha }$
for all
![]() $\alpha \leq \kappa $
, and that
$\alpha \leq \kappa $
, and that
![]() $\mathbb {P}_{\beta }$
is a sub-poset of
$\mathbb {P}_{\beta }$
is a sub-poset of
![]() $\mathbb {P}_{\alpha }$
whenever
$\mathbb {P}_{\alpha }$
whenever
![]() $\beta \leq \alpha \leq \kappa $
.
$\beta \leq \alpha \leq \kappa $
.
Lemma 3.6.
![]() $\mathbb {P}_{\beta }$
is a complete sub-poset of
$\mathbb {P}_{\beta }$
is a complete sub-poset of
![]() $\mathbb {P}_{\alpha }$
for all
$\mathbb {P}_{\alpha }$
for all
![]() $\beta \leq \alpha \leq \kappa $
.
$\beta \leq \alpha \leq \kappa $
.
Proof Fix
![]() $\beta \leq \alpha \leq \kappa $
. By definition, the ordering
$\beta \leq \alpha \leq \kappa $
. By definition, the ordering
![]() $\leq _{\beta }$
on
$\leq _{\beta }$
on
![]() $\mathbb {P}_{\beta }$
is equal to the ordering
$\mathbb {P}_{\beta }$
is equal to the ordering
![]() $\leq _{\alpha }$
on
$\leq _{\alpha }$
on
![]() $\mathbb {P}_{\alpha }$
restricted to
$\mathbb {P}_{\alpha }$
restricted to
![]() $\mathbb {P}_{\beta }$
. So to prove the lemma, it suffices to show that every maximal antichain in
$\mathbb {P}_{\beta }$
. So to prove the lemma, it suffices to show that every maximal antichain in
![]() $\mathbb {P}_{\beta }$
is also a maximal antichain in
$\mathbb {P}_{\beta }$
is also a maximal antichain in
![]() $\mathbb {P}_{\alpha }$
. Suppose
$\mathbb {P}_{\alpha }$
. Suppose
![]() $\mathcal {A}$
is a maximal antichain in
$\mathcal {A}$
is a maximal antichain in
![]() $\mathbb {P}_{\beta }$
, and let
$\mathbb {P}_{\beta }$
, and let
![]() $p \in \mathbb {P}_{\alpha }$
. By the maximality of
$p \in \mathbb {P}_{\alpha }$
. By the maximality of
![]() $\mathcal {A}$
, there is some
$\mathcal {A}$
, there is some
![]() $q \in \mathcal {A}$
such that q is compatible with
$q \in \mathcal {A}$
such that q is compatible with
![]() $p \!\restriction \! \beta $
in
$p \!\restriction \! \beta $
in
![]() $\mathbb {P}_{\beta }$
. Let
$\mathbb {P}_{\beta }$
. Let
![]() $r \in \mathbb {P}_{\beta }$
be a common extension of q and
$r \in \mathbb {P}_{\beta }$
be a common extension of q and
![]() $p \!\restriction \! \beta $
. Define a function s on
$p \!\restriction \! \beta $
. Define a function s on
![]() $(I \times \omega ) \cup (\alpha \times \mathcal {C} \times \omega )$
by setting
$(I \times \omega ) \cup (\alpha \times \mathcal {C} \times \omega )$
by setting
![]() $s=r$
on
$s=r$
on
![]() $(I \times \omega ) \cup (\beta \times \mathcal {C} \times \omega )$
and setting
$(I \times \omega ) \cup (\beta \times \mathcal {C} \times \omega )$
and setting
![]() $s=p$
on
$s=p$
on
![]() $(I \times \omega ) \cup ((\alpha \setminus \beta ) \times \mathcal {C} \times \omega )$
. Then
$(I \times \omega ) \cup ((\alpha \setminus \beta ) \times \mathcal {C} \times \omega )$
. Then
![]() $s \in \mathbb {P}_{\alpha }$
, and s is a common extension of p and q in
$s \in \mathbb {P}_{\alpha }$
, and s is a common extension of p and q in
![]() $\mathbb {P}_{\alpha }$
. As p was arbitrary, this shows
$\mathbb {P}_{\alpha }$
. As p was arbitrary, this shows
![]() $\mathcal {A}$
is a maximal antichain in
$\mathcal {A}$
is a maximal antichain in
![]() $\mathbb {P}_{\alpha }$
.
$\mathbb {P}_{\alpha }$
.
Lemma 3.7.
![]() $\mathbb {P}_{\kappa }$
has the ccc.
$\mathbb {P}_{\kappa }$
has the ccc.
Proof Let
![]() $\mathcal {A}_0$
be an uncountable subset of
$\mathcal {A}_0$
be an uncountable subset of
![]() $\mathbb {P}_{\kappa }$
. By the
$\mathbb {P}_{\kappa }$
. By the
![]() $\Delta $
-system lemma, there is an uncountable
$\Delta $
-system lemma, there is an uncountable
![]() $\mathcal {A}_1 \subseteq \mathcal {A}_0$
and a finite
$\mathcal {A}_1 \subseteq \mathcal {A}_0$
and a finite
![]() $R \subseteq (I \times \omega ) \cup (\kappa \times C \times \omega )$
such that for any
$R \subseteq (I \times \omega ) \cup (\kappa \times C \times \omega )$
such that for any
![]() $p,q \in \mathcal {A}_1$
,
$p,q \in \mathcal {A}_1$
,
![]() $\mathrm {dom}(p) \cap \mathrm {dom}(p) = R$
. If
$\mathrm {dom}(p) \cap \mathrm {dom}(p) = R$
. If
![]() $i \in R \cap (I \times \omega )$
, then
$i \in R \cap (I \times \omega )$
, then
![]() $p(i) \in \{0,1\}$
for every
$p(i) \in \{0,1\}$
for every
![]() $p \in \mathcal {A}_1$
. As there are only finitely many functions
$p \in \mathcal {A}_1$
. As there are only finitely many functions
![]() $R \cap (I \times \omega ) \to 2$
, this implies there is some uncountable
$R \cap (I \times \omega ) \to 2$
, this implies there is some uncountable
![]() $\mathcal {A}_2 \subseteq \mathcal {A}_1$
such that
$\mathcal {A}_2 \subseteq \mathcal {A}_1$
such that
![]() $p \!\restriction \! (R \cap (I \times \omega )) = q \!\restriction \! (R \cap (I \times \omega ))$
for any
$p \!\restriction \! (R \cap (I \times \omega )) = q \!\restriction \! (R \cap (I \times \omega ))$
for any
![]() $p,q \in \mathcal {A}_2$
. For every
$p,q \in \mathcal {A}_2$
. For every
![]() $p \in \mathcal {A}_2$
, if
$p \in \mathcal {A}_2$
, if
![]() $j \in R \setminus (I \times \omega )$
, then
$j \in R \setminus (I \times \omega )$
, then
![]() $p(j) = (t,B)$
for some finite subtree t of
$p(j) = (t,B)$
for some finite subtree t of
![]() $2^{<\omega }$
. As there are only countably many finite subtrees of
$2^{<\omega }$
. As there are only countably many finite subtrees of
![]() $2^{<\omega }$
, there is some uncountable
$2^{<\omega }$
, there is some uncountable
![]() $\mathcal {A}_3 \subseteq \mathcal {A}_2$
such that for each
$\mathcal {A}_3 \subseteq \mathcal {A}_2$
such that for each
![]() $j \in R \setminus (I \times \omega )$
, there is some fixed
$j \in R \setminus (I \times \omega )$
, there is some fixed
![]() $t_j$
such that for any
$t_j$
such that for any
![]() $p \in \mathcal {A}_3$
,
$p \in \mathcal {A}_3$
,
![]() $p(j) = (t_j,B^p_j)$
for some
$p(j) = (t_j,B^p_j)$
for some
![]() $B^p_j$
. But any two members of
$B^p_j$
. But any two members of
![]() $\mathcal {A}_3$
are compatible: if
$\mathcal {A}_3$
are compatible: if
![]() $p,q \in \mathcal {A}_3$
, then
$p,q \in \mathcal {A}_3$
, then
 $$ \begin{align*}r(j)= \begin{cases} p(j), & \text{ if } j \in \mathrm{dom}(p) \setminus R, \\ q(j), & \text{ if } j \in \mathrm{dom}(q) \setminus R, \\ (t_j,B^p_j \cup B^q_j), & \text{ if } j \in \mathrm{dom}(p) \cap \mathrm{dom}(q) = R \end{cases} \end{align*} $$
$$ \begin{align*}r(j)= \begin{cases} p(j), & \text{ if } j \in \mathrm{dom}(p) \setminus R, \\ q(j), & \text{ if } j \in \mathrm{dom}(q) \setminus R, \\ (t_j,B^p_j \cup B^q_j), & \text{ if } j \in \mathrm{dom}(p) \cap \mathrm{dom}(q) = R \end{cases} \end{align*} $$
is a common extension of p and q. Thus
![]() $\mathbb {P}_{\kappa }$
has no uncountable antichains, and is ccc. (In fact we have shown a bit more:
$\mathbb {P}_{\kappa }$
has no uncountable antichains, and is ccc. (In fact we have shown a bit more:
![]() $\mathbb {P}_{\kappa }$
has property K.)
$\mathbb {P}_{\kappa }$
has property K.)
If
![]() $\beta \leq \alpha $
, then because
$\beta \leq \alpha $
, then because
![]() $\mathbb {P}_{\beta } \subseteq \mathbb {P}_{\alpha }$
, we may (and do) consider every
$\mathbb {P}_{\beta } \subseteq \mathbb {P}_{\alpha }$
, we may (and do) consider every
![]() $\mathbb {P}_{\beta }$
-name to be a
$\mathbb {P}_{\beta }$
-name to be a
![]() $\mathbb {P}_{\alpha }$
-name as well. Let us also set the convention that in
$\mathbb {P}_{\alpha }$
-name as well. Let us also set the convention that in
![]() $V^{\mathbb {P}_{\alpha }}$
, the evaluation of a
$V^{\mathbb {P}_{\alpha }}$
, the evaluation of a
![]() $\mathbb {P}_{\alpha }$
-name is indicated by removing its dot. So, for example,
$\mathbb {P}_{\alpha }$
-name is indicated by removing its dot. So, for example,
![]() $c_i$
denotes in
$c_i$
denotes in
![]() $V^{\mathbb {P}_{\alpha }}$
(for any
$V^{\mathbb {P}_{\alpha }}$
(for any
![]() $\alpha \leq \kappa $
) the Cohen real added by
$\alpha \leq \kappa $
) the Cohen real added by
![]() $\mathbb {P}_0$
in coordinate i, and
$\mathbb {P}_0$
in coordinate i, and
![]() $T^{\xi }_{\mu ,n}$
denotes in
$T^{\xi }_{\mu ,n}$
denotes in
![]() $V^{\mathbb {P}_{\alpha }}$
, for any
$V^{\mathbb {P}_{\alpha }}$
, for any
![]() $\alpha \geq \xi $
, the evaluation of the name
$\alpha \geq \xi $
, the evaluation of the name
![]() $\dot T^{\xi }_{\mu ,n}$
.
$\dot T^{\xi }_{\mu ,n}$
.
Lemma 3.8.
![]() $C \subseteq \mathfrak {sp}({\small\text{closed}})$
in
$C \subseteq \mathfrak {sp}({\small\text{closed}})$
in
![]() $V^{\mathbb {P}_{\kappa }}$
.
$V^{\mathbb {P}_{\kappa }}$
.
Proof Let
![]() $\mu \in C$
. We claim that in
$\mu \in C$
. We claim that in
![]() $V^{\mathbb {P}_{\kappa }}$
,
$V^{\mathbb {P}_{\kappa }}$
,
is a partition of
![]() $2^{\omega }$
. Observe that every member of
$2^{\omega }$
. Observe that every member of
![]() $\mathcal {P}$
is an
$\mathcal {P}$
is an
![]() $F_{\sigma }$
subset of
$F_{\sigma }$
subset of
![]() $2^{\omega }$
, and
$2^{\omega }$
, and
![]() $|\mathcal {P}| = \mu $
. (It is clear that each
$|\mathcal {P}| = \mu $
. (It is clear that each
![]() $T^{\alpha }_{\mu ,n}$
is a subtree of
$T^{\alpha }_{\mu ,n}$
is a subtree of
![]() $2^{<\omega }$
, which means the sets of the form
$2^{<\omega }$
, which means the sets of the form
![]() $\bigcup _{n \in \omega } [\![T^{\alpha }_{\mu ,n}]\!]$
are all
$\bigcup _{n \in \omega } [\![T^{\alpha }_{\mu ,n}]\!]$
are all
![]() $F_{\sigma }$
.) Thus if
$F_{\sigma }$
.) Thus if
![]() $\mathcal {P}$
is a partition, then
$\mathcal {P}$
is a partition, then
![]() $\mu \in \mathfrak {sp}({\small\text{closed}})$
by Theorem 2.4.
$\mu \in \mathfrak {sp}({\small\text{closed}})$
by Theorem 2.4.
The members of
![]() $\mathcal {P}$
come in two types, so in order to show they are pairwise disjoint, we have three things to prove.
$\mathcal {P}$
come in two types, so in order to show they are pairwise disjoint, we have three things to prove.
First, if
![]() $i,i' \in I_{\mu }$
and
$i,i' \in I_{\mu }$
and
![]() $i \neq i'$
, then clearly
$i \neq i'$
, then clearly
![]() $c_i \neq c_{i'}$
, i.e.,
$c_i \neq c_{i'}$
, i.e.,
![]() $\{c_i\} \cap \{c_{i'}\} = \emptyset $
.
$\{c_i\} \cap \{c_{i'}\} = \emptyset $
.
Second, fix
![]() $i \in I_{\mu }$
,
$i \in I_{\mu }$
,
![]() $\alpha < \kappa $
, and
$\alpha < \kappa $
, and
![]() $n \in \omega $
. We claim
$n \in \omega $
. We claim
![]() $\{c_i\} \cap [\![T^{\alpha }_{\mu ,n}]\!] = \emptyset $
, or equivalently,
$\{c_i\} \cap [\![T^{\alpha }_{\mu ,n}]\!] = \emptyset $
, or equivalently,
![]() $c_i \notin [\![T^{\alpha }_{\mu ,n}]\!]$
. To see this, fix some
$c_i \notin [\![T^{\alpha }_{\mu ,n}]\!]$
. To see this, fix some
![]() $p \in \mathbb {P}_{\kappa }$
: we will find an extension r of p forcing
$p \in \mathbb {P}_{\kappa }$
: we will find an extension r of p forcing
![]() $c_i \notin [\![T^{\alpha }_{\mu ,n}]\!]$
. Extending p to
$c_i \notin [\![T^{\alpha }_{\mu ,n}]\!]$
. Extending p to
![]() $p \cup \{\langle (\alpha ,\mu ,n),(\emptyset ,\emptyset ) \rangle \}$
, if necessary, we may (and do) assume
$p \cup \{\langle (\alpha ,\mu ,n),(\emptyset ,\emptyset ) \rangle \}$
, if necessary, we may (and do) assume
![]() $(\alpha ,\mu ,n) \in \mathrm {dom}(p)$
. Let
$(\alpha ,\mu ,n) \in \mathrm {dom}(p)$
. Let
![]() $(t,B) = p(\alpha ,\mu ,n)$
, with t a pruned subtree of
$(t,B) = p(\alpha ,\mu ,n)$
, with t a pruned subtree of
![]() $2^{<k}$
. From the definition of
$2^{<k}$
. From the definition of
![]() $\mathbb {P}_{\kappa }$
, we know
$\mathbb {P}_{\kappa }$
, we know
![]() $p \!\restriction \! \alpha \Vdash _{\mathbb {P}_{\alpha }} \dot b \neq \dot c_i$
for every
$p \!\restriction \! \alpha \Vdash _{\mathbb {P}_{\alpha }} \dot b \neq \dot c_i$
for every
![]() $\dot b \in B$
. Using this, and the fact that B is finite, there is an extension q of p in
$\dot b \in B$
. Using this, and the fact that B is finite, there is an extension q of p in
![]() $\mathbb {P}_{\alpha }$
, and some finite sequence
$\mathbb {P}_{\alpha }$
, and some finite sequence
![]() $\sigma \in 2^{\ell }$
for some
$\sigma \in 2^{\ell }$
for some
![]() $\ell> k$
, such that
$\ell> k$
, such that
![]() $q \Vdash _{\mathbb {P}_{\alpha }}$
“
$q \Vdash _{\mathbb {P}_{\alpha }}$
“
![]() $\dot c_i \!\restriction \! \ell = \sigma $
but
$\dot c_i \!\restriction \! \ell = \sigma $
but
![]() $\dot b \!\restriction \! \ell \neq \sigma $
for all
$\dot b \!\restriction \! \ell \neq \sigma $
for all
![]() $\dot b \in B$
.” Let
$\dot b \in B$
.” Let
![]() $t'$
be the largest subtree of
$t'$
be the largest subtree of
![]() $2^{<\ell +1}$
that is an end extension of t and that does not contain
$2^{<\ell +1}$
that is an end extension of t and that does not contain
![]() $\sigma $
. (In other words,
$\sigma $
. (In other words,
![]() $\tau \in t'$
if and only if
$\tau \in t'$
if and only if
![]() $\tau \in 2^{<\ell +1} \setminus \{\sigma \}$
and
$\tau \in 2^{<\ell +1} \setminus \{\sigma \}$
and
![]() $\tau \!\restriction \! k \in t$
. This is a subtree of
$\tau \!\restriction \! k \in t$
. This is a subtree of
![]() $2^{<\ell +1}$
, and it is an end extension of t because
$2^{<\ell +1}$
, and it is an end extension of t because
![]() $\ell> k$
and
$\ell> k$
and
![]() $\sigma \in 2^{\ell }$
.) Define a function r on
$\sigma \in 2^{\ell }$
.) Define a function r on
![]() $(I \times \omega ) \cup (\kappa \times \mathcal {C} \times \omega )$
by setting
$(I \times \omega ) \cup (\kappa \times \mathcal {C} \times \omega )$
by setting
 $$ \begin{align*}r(j)= \begin{cases} q(j), & \text{ if } j \in (I \times \omega) \cup (\alpha \times \mathcal{C} \times \omega), \\ p(j), & \text{ if } j \in (I \times \omega) \cup ((\kappa \setminus \alpha) \times \mathcal{C} \times \omega) \text{ but } j \neq (\alpha,\mu,n)), \\ (t',B), & \text{ if } j = (\alpha,\mu,n). \end{cases} \end{align*} $$
$$ \begin{align*}r(j)= \begin{cases} q(j), & \text{ if } j \in (I \times \omega) \cup (\alpha \times \mathcal{C} \times \omega), \\ p(j), & \text{ if } j \in (I \times \omega) \cup ((\kappa \setminus \alpha) \times \mathcal{C} \times \omega) \text{ but } j \neq (\alpha,\mu,n)), \\ (t',B), & \text{ if } j = (\alpha,\mu,n). \end{cases} \end{align*} $$
Then
![]() $r \in \mathbb {P}_{\kappa }$
, and
$r \in \mathbb {P}_{\kappa }$
, and
![]() $r \Vdash \sigma \notin \dot T^{\alpha }_{\mu ,n}$
and
$r \Vdash \sigma \notin \dot T^{\alpha }_{\mu ,n}$
and
![]() $\dot c_i \!\restriction \! \ell = \sigma $
, which means
$\dot c_i \!\restriction \! \ell = \sigma $
, which means
![]() $r \Vdash \dot c_i \notin [\![\dot T^{\alpha }_{\mu ,n}]\!]$
. As p was arbitrary, this shows that
$r \Vdash \dot c_i \notin [\![\dot T^{\alpha }_{\mu ,n}]\!]$
. As p was arbitrary, this shows that
![]() $c_i \notin [\![T^{\alpha }_{\mu ,n}]\!]$
in
$c_i \notin [\![T^{\alpha }_{\mu ,n}]\!]$
in
![]() $V^{\mathbb {P}_{\kappa }}$
.
$V^{\mathbb {P}_{\kappa }}$
.
Third, fix
![]() $\beta < \alpha < \kappa $
, and
$\beta < \alpha < \kappa $
, and
![]() $m,n \in \omega $
. We claim that
$m,n \in \omega $
. We claim that
![]() $[\![T^{\beta }_{\mu ,m}]\!] \cap [\![T^{\alpha }_{\mu ,n}]\!] = \emptyset $
. To see this, fix
$[\![T^{\beta }_{\mu ,m}]\!] \cap [\![T^{\alpha }_{\mu ,n}]\!] = \emptyset $
. To see this, fix
![]() $p \in \mathbb {P}_{\kappa }$
: we will find an extension of p forcing
$p \in \mathbb {P}_{\kappa }$
: we will find an extension of p forcing
![]() $[\![T^{\beta }_{\mu ,m}]\!] \cap [\![T^{\alpha }_{\mu ,n}]\!] = \emptyset $
. Extending p to
$[\![T^{\beta }_{\mu ,m}]\!] \cap [\![T^{\alpha }_{\mu ,n}]\!] = \emptyset $
. Extending p to
![]() $p \cup \{\langle (\beta ,\mu ,m),(\emptyset ,\emptyset ) \rangle ,\langle (\alpha ,\mu ,n),(\emptyset ,\emptyset ) \rangle \}$
, if necessary, we may (and do) assume
$p \cup \{\langle (\beta ,\mu ,m),(\emptyset ,\emptyset ) \rangle ,\langle (\alpha ,\mu ,n),(\emptyset ,\emptyset ) \rangle \}$
, if necessary, we may (and do) assume
![]() $(\beta ,\mu ,m),(\alpha ,\mu ,n) \in \mathrm {dom}(p)$
. Let
$(\beta ,\mu ,m),(\alpha ,\mu ,n) \in \mathrm {dom}(p)$
. Let
![]() $(t_{\beta },B_{\beta }) = p(\beta ,\mu ,m)$
, where
$(t_{\beta },B_{\beta }) = p(\beta ,\mu ,m)$
, where
![]() $t_{\beta }$
is a pruned subtree of
$t_{\beta }$
is a pruned subtree of
![]() $2^{<k_{\beta }}$
for some
$2^{<k_{\beta }}$
for some
![]() $k_{\beta } \in \omega $
, and let
$k_{\beta } \in \omega $
, and let
![]() $(t_{\alpha },B_{\alpha }) = p(\alpha ,\mu ,n)$
, where
$(t_{\alpha },B_{\alpha }) = p(\alpha ,\mu ,n)$
, where
![]() $t_{\alpha }$
is a pruned subtree of
$t_{\alpha }$
is a pruned subtree of
![]() $2^{<k_{\alpha }}$
for some
$2^{<k_{\alpha }}$
for some
![]() $k_{\alpha } \in \omega $
. From the definition of
$k_{\alpha } \in \omega $
. From the definition of
![]() $\mathbb {P}_{\kappa }$
, we know that
$\mathbb {P}_{\kappa }$
, we know that
![]() $p \!\restriction \! ((I \times \omega ) \cup (\alpha \times C \times \omega )) \Vdash _{\mathbb {P}_{\alpha }} \dot b \neq \dot a$
for every
$p \!\restriction \! ((I \times \omega ) \cup (\alpha \times C \times \omega )) \Vdash _{\mathbb {P}_{\alpha }} \dot b \neq \dot a$
for every
![]() $\dot b \in B_{\beta }$
and
$\dot b \in B_{\beta }$
and
![]() $\dot a \in B_{\alpha }$
. Using this, and the fact that
$\dot a \in B_{\alpha }$
. Using this, and the fact that
![]() $B_{\beta }$
and
$B_{\beta }$
and
![]() $B_{\alpha }$
are both finite, there is an extension q of p in
$B_{\alpha }$
are both finite, there is an extension q of p in
![]() $\mathbb {P}_{\alpha }$
, and some
$\mathbb {P}_{\alpha }$
, and some
![]() $\ell> k_{\beta },k_{\alpha }$
, such that q “decides” all the
$\ell> k_{\beta },k_{\alpha }$
, such that q “decides” all the
![]() $\dot b$
and
$\dot b$
and
![]() $\dot a$
up to
$\dot a$
up to
![]() $\ell $
, and in such a way that witnesses
$\ell $
, and in such a way that witnesses
![]() $\dot b \neq \dot a$
for all
$\dot b \neq \dot a$
for all
![]() $\dot b \in B_{\beta }$
and
$\dot b \in B_{\beta }$
and
![]() $\dot a \in B_{\alpha }$
. More precisely: for each
$\dot a \in B_{\alpha }$
. More precisely: for each
![]() $\dot b \in B_{\beta }$
, there is a particular branch
$\dot b \in B_{\beta }$
, there is a particular branch
![]() $c(\dot b)$
of
$c(\dot b)$
of
![]() $2^{<\ell +1}$
such that
$2^{<\ell +1}$
such that
![]() $q \Vdash _{\mathbb {P}_{\alpha }}$
“
$q \Vdash _{\mathbb {P}_{\alpha }}$
“
![]() $\dot b \!\restriction \! \ell = c(\dot b)$
”; and similarly, for each
$\dot b \!\restriction \! \ell = c(\dot b)$
”; and similarly, for each
![]() $\dot a \in B_{\alpha }$
, there is a particular branch
$\dot a \in B_{\alpha }$
, there is a particular branch
![]() $c(\dot a)$
of
$c(\dot a)$
of
![]() $2^{<\ell +1}$
such that
$2^{<\ell +1}$
such that
![]() $q \Vdash _{\mathbb {P}_{\alpha }}$
“
$q \Vdash _{\mathbb {P}_{\alpha }}$
“
![]() $\dot a \!\restriction \! \ell = c(\dot a)$
”; and furthermore,
$\dot a \!\restriction \! \ell = c(\dot a)$
”; and furthermore,
![]() $c(\dot b) \!\restriction \! \ell \neq c(\dot a) \!\restriction \! \ell $
for all
$c(\dot b) \!\restriction \! \ell \neq c(\dot a) \!\restriction \! \ell $
for all
![]() $\dot b \in B_{\beta }$
and
$\dot b \in B_{\beta }$
and
![]() $\dot a \in B_{\alpha }$
. Let
$\dot a \in B_{\alpha }$
. Let
![]() $t^{\prime }_{\beta }$
be the largest end extension of
$t^{\prime }_{\beta }$
be the largest end extension of
![]() $t_{\beta }$
that is a pruned subtree of
$t_{\beta }$
that is a pruned subtree of
![]() $2^{<\ell }$
, and let
$2^{<\ell }$
, and let
![]() $t^{\prime \prime }_{\beta }$
be the end extension of
$t^{\prime \prime }_{\beta }$
be the end extension of
![]() $t^{\prime }_{\beta }$
to a pruned subtree of
$t^{\prime }_{\beta }$
to a pruned subtree of
![]() $2^{<\ell +1}$
containing on level
$2^{<\ell +1}$
containing on level
![]() $\ell $
the nodes:
$\ell $
the nodes:
 $$ \begin{align*} \sigma \!\,^{\frown} 0 \quad & \text{ if } \sigma \in t^{\prime}_{\beta}, \sigma = c(\dot a) \text{ for some } \dot a \in B_{\alpha}, \text{ and } c(\dot a)(\ell) = 1, \\ \sigma \!\,^{\frown} 1 \quad & \text{ if } \sigma \in t^{\prime}_{\beta}, \sigma = c(\dot a) \text{ for some } \dot a \in B_{\alpha}, \text{ and } c(\dot a)(\ell) = 0, \\ \sigma \!\,^{\frown} 0 \quad & \text{ if } \sigma \in t^{\prime}_{\beta} \text{ and } \sigma \neq c(\dot a) \text{ for any } \dot a \in B_{\alpha}. \end{align*} $$
$$ \begin{align*} \sigma \!\,^{\frown} 0 \quad & \text{ if } \sigma \in t^{\prime}_{\beta}, \sigma = c(\dot a) \text{ for some } \dot a \in B_{\alpha}, \text{ and } c(\dot a)(\ell) = 1, \\ \sigma \!\,^{\frown} 1 \quad & \text{ if } \sigma \in t^{\prime}_{\beta}, \sigma = c(\dot a) \text{ for some } \dot a \in B_{\alpha}, \text{ and } c(\dot a)(\ell) = 0, \\ \sigma \!\,^{\frown} 0 \quad & \text{ if } \sigma \in t^{\prime}_{\beta} \text{ and } \sigma \neq c(\dot a) \text{ for any } \dot a \in B_{\alpha}. \end{align*} $$
Similarly, let
![]() $t^{\prime }_{\alpha }$
be the largest end extension of
$t^{\prime }_{\alpha }$
be the largest end extension of
![]() $t_{\alpha }$
that is a pruned subtree of
$t_{\alpha }$
that is a pruned subtree of
![]() $2^{<\ell }$
, and let
$2^{<\ell }$
, and let
![]() $t^{\prime \prime }_{\alpha }$
be the end extension of
$t^{\prime \prime }_{\alpha }$
be the end extension of
![]() $t^{\prime }_{\alpha }$
to a pruned subtree of
$t^{\prime }_{\alpha }$
to a pruned subtree of
![]() $2^{<\ell +1}$
containing on level
$2^{<\ell +1}$
containing on level
![]() $\ell $
the nodes:
$\ell $
the nodes:
 $$ \begin{align*} \sigma \!\,^{\frown} 0 \quad & \text{ if } \sigma \in t^{\prime}_{\alpha}, \sigma = c(\dot b) \text{ for some } \dot b \in B_{\beta}, \text{ and } c(\dot b)(\ell) = 1, \\ \sigma \!\,^{\frown} 1 \quad & \text{ if } \sigma \in t^{\prime}_{\alpha}, \sigma = c(\dot b) \text{ for some } \dot b \in B_{\beta}, \text{ and } c(\dot b)(\ell) = 0, \\ \sigma \!\,^{\frown} 1 \quad & \text{ if } \sigma \in t^{\prime}_{\alpha} \text{ and } \sigma \neq c(\dot b) \text{ for any } \dot b \in B_{\beta}. \end{align*} $$
$$ \begin{align*} \sigma \!\,^{\frown} 0 \quad & \text{ if } \sigma \in t^{\prime}_{\alpha}, \sigma = c(\dot b) \text{ for some } \dot b \in B_{\beta}, \text{ and } c(\dot b)(\ell) = 1, \\ \sigma \!\,^{\frown} 1 \quad & \text{ if } \sigma \in t^{\prime}_{\alpha}, \sigma = c(\dot b) \text{ for some } \dot b \in B_{\beta}, \text{ and } c(\dot b)(\ell) = 0, \\ \sigma \!\,^{\frown} 1 \quad & \text{ if } \sigma \in t^{\prime}_{\alpha} \text{ and } \sigma \neq c(\dot b) \text{ for any } \dot b \in B_{\beta}. \end{align*} $$
Observe that
![]() $t^{\prime \prime }_{\beta }$
and
$t^{\prime \prime }_{\beta }$
and
![]() $t^{\prime \prime }_{\alpha }$
have no common nodes on level
$t^{\prime \prime }_{\alpha }$
have no common nodes on level
![]() $\ell $
. Define a function r on
$\ell $
. Define a function r on
![]() $(I \times \omega ) \cup (\kappa \times \mathcal {C} \times \omega )$
by setting
$(I \times \omega ) \cup (\kappa \times \mathcal {C} \times \omega )$
by setting
 $$ \begin{align*}r(j)= \begin{cases} q(j), & \text{ if } j \in (I \times \omega) \cup (\alpha \times \mathcal{C} \times \omega) \text{ but } j \neq (\beta,\mu,m), \\ p(j), & \text{ if } j \in (I \times \omega) \cup ((\kappa \setminus \alpha) \times \mathcal{C} \times \omega)) \text{ but } j \neq (\alpha,\mu,n), \\ (t^{\prime\prime}_{\beta},B_{\beta}), & \text{ if } j = (\beta,\mu,m), \\ (t^{\prime\prime}_{\alpha},B_{\alpha}), & \text{ if } j = (\alpha,\mu,n). \end{cases} \end{align*} $$
$$ \begin{align*}r(j)= \begin{cases} q(j), & \text{ if } j \in (I \times \omega) \cup (\alpha \times \mathcal{C} \times \omega) \text{ but } j \neq (\beta,\mu,m), \\ p(j), & \text{ if } j \in (I \times \omega) \cup ((\kappa \setminus \alpha) \times \mathcal{C} \times \omega)) \text{ but } j \neq (\alpha,\mu,n), \\ (t^{\prime\prime}_{\beta},B_{\beta}), & \text{ if } j = (\beta,\mu,m), \\ (t^{\prime\prime}_{\alpha},B_{\alpha}), & \text{ if } j = (\alpha,\mu,n). \end{cases} \end{align*} $$
Then
![]() $r \in \mathbb {P}_{\kappa }$
, and
$r \in \mathbb {P}_{\kappa }$
, and
![]() $r \Vdash t^{\prime \prime }_{\beta }$
is a subtree of
$r \Vdash t^{\prime \prime }_{\beta }$
is a subtree of
![]() $\dot T^{\beta }_{\mu ,m}$
and
$\dot T^{\beta }_{\mu ,m}$
and
![]() $r \Vdash t^{\prime \prime }_{\alpha }$
is a subtree of
$r \Vdash t^{\prime \prime }_{\alpha }$
is a subtree of
![]() $\dot T^{\alpha }_{\mu ,n}$
. Because
$\dot T^{\alpha }_{\mu ,n}$
. Because
![]() $t^{\prime \prime }_{\beta }$
and
$t^{\prime \prime }_{\beta }$
and
![]() $t^{\prime \prime }_{\alpha }$
share no nodes on level
$t^{\prime \prime }_{\alpha }$
share no nodes on level
![]() $\ell $
,
$\ell $
,
![]() $r \Vdash [\![\dot T^{\beta }_{\mu ,m}]\!] \cap [\![\dot T^{\alpha }_{\mu ,n}]\!] = \emptyset $
. As p was arbitrary, this shows that
$r \Vdash [\![\dot T^{\beta }_{\mu ,m}]\!] \cap [\![\dot T^{\alpha }_{\mu ,n}]\!] = \emptyset $
. As p was arbitrary, this shows that
![]() $[\![T^{\beta }_{\mu ,m}]\!] \cap [\![T^{\alpha }_{\mu ,n}]\!] = \emptyset $
in
$[\![T^{\beta }_{\mu ,m}]\!] \cap [\![T^{\alpha }_{\mu ,n}]\!] = \emptyset $
in
![]() $V^{\mathbb {P}_{\kappa }}$
.
$V^{\mathbb {P}_{\kappa }}$
.
Thus
![]() $\mathcal {P}$
is a pairwise disjoint collection of
$\mathcal {P}$
is a pairwise disjoint collection of
![]() $F_{\sigma }$
subsets of
$F_{\sigma }$
subsets of
![]() $2^{\omega }$
in
$2^{\omega }$
in
![]() $V^{\mathbb {P}_{\kappa }}$
. To finish the proof, we must show also that
$V^{\mathbb {P}_{\kappa }}$
. To finish the proof, we must show also that
![]() $\bigcup \mathcal {P} = 2^{\omega }$
.
$\bigcup \mathcal {P} = 2^{\omega }$
.
Fix
![]() $x \in 2^{\omega }$
in
$x \in 2^{\omega }$
in
![]() $V^{\mathbb {P}_{\kappa }}$
. Because
$V^{\mathbb {P}_{\kappa }}$
. Because
![]() $\mathbb {P}_{\kappa }$
has the ccc, and each
$\mathbb {P}_{\kappa }$
has the ccc, and each
![]() $\mathbb {P}_{\alpha }$
is a complete sub-poset of
$\mathbb {P}_{\alpha }$
is a complete sub-poset of
![]() $\mathbb {P}_{\kappa }$
, there is some
$\mathbb {P}_{\kappa }$
, there is some
![]() $\alpha < \kappa $
such that
$\alpha < \kappa $
such that
![]() $x \in V^{\mathbb {P}_{\alpha }}$
. If
$x \in V^{\mathbb {P}_{\alpha }}$
. If
![]() $x = c_i$
for some
$x = c_i$
for some
![]() $i \in I_{\mu }$
, or if
$i \in I_{\mu }$
, or if
![]() $x \in [\![T^{\xi }_{\mu ,n}]\!]$
for some
$x \in [\![T^{\xi }_{\mu ,n}]\!]$
for some
![]() $\xi < \alpha $
, then we’re done. If not, let
$\xi < \alpha $
, then we’re done. If not, let
![]() $\dot x$
be a nice
$\dot x$
be a nice
![]() $\mathbb {P}_{\alpha }$
-name for x, and fix some
$\mathbb {P}_{\alpha }$
-name for x, and fix some
![]() $p \in \mathbb {P}_{\kappa }$
such that
$p \in \mathbb {P}_{\kappa }$
such that
![]() $p \Vdash $
“
$p \Vdash $
“
![]() $\dot x \neq \dot c_i$
for all
$\dot x \neq \dot c_i$
for all
![]() $i \in I_{\mu }$
, and
$i \in I_{\mu }$
, and
![]() $\dot x \notin [\![\dot T^{\xi }_{\mu ,n}]\!]$
for all
$\dot x \notin [\![\dot T^{\xi }_{\mu ,n}]\!]$
for all
![]() $\xi < \alpha $
and
$\xi < \alpha $
and
![]() $n \in \omega $
.” Because p has finite support, there is some
$n \in \omega $
.” Because p has finite support, there is some
![]() $N \in \omega $
such that
$N \in \omega $
such that
![]() $(\alpha ,\mu ,N) \notin \mathrm {dom}(p)$
. But then
$(\alpha ,\mu ,N) \notin \mathrm {dom}(p)$
. But then
![]() $q = p \cup \{ \langle (\alpha ,\mu ,N),(\emptyset ,\{\dot x\}) \rangle \}$
is in
$q = p \cup \{ \langle (\alpha ,\mu ,N),(\emptyset ,\{\dot x\}) \rangle \}$
is in
![]() $\mathbb {P}_{\alpha }$
, and
$\mathbb {P}_{\alpha }$
, and
![]() $q \Vdash \dot x \in [\![\dot T^{\alpha }_{\mu ,N}]\!]$
. Thus for every condition p forcing
$q \Vdash \dot x \in [\![\dot T^{\alpha }_{\mu ,N}]\!]$
. Thus for every condition p forcing
![]() $x \notin \bigcup _{i \in I_{\mu }}\{c_i\} \cup \bigcup _{\xi < \alpha }\bigcup _{n \in \omega }[\![T^{\xi }_{\mu ,n}]\!]$
, there is an extension q of p forcing
$x \notin \bigcup _{i \in I_{\mu }}\{c_i\} \cup \bigcup _{\xi < \alpha }\bigcup _{n \in \omega }[\![T^{\xi }_{\mu ,n}]\!]$
, there is an extension q of p forcing
![]() $x \in \bigcup _{n \in \omega }[\![T^{\alpha }_{\mu ,n}]\!]$
. Hence
$x \in \bigcup _{n \in \omega }[\![T^{\alpha }_{\mu ,n}]\!]$
. Hence
![]() $x \in \bigcup _{i \in I_{\mu }}\{c_i\} \cup \bigcup _{\xi \leq \alpha }\bigcup _{n \in \omega }[\![T^{\xi }_{\mu ,n}]\!] \subseteq \bigcup \mathcal {P}$
. As x was arbitrary,
$x \in \bigcup _{i \in I_{\mu }}\{c_i\} \cup \bigcup _{\xi \leq \alpha }\bigcup _{n \in \omega }[\![T^{\xi }_{\mu ,n}]\!] \subseteq \bigcup \mathcal {P}$
. As x was arbitrary,
![]() $\bigcup \mathcal {P} = 2^{\omega }$
as claimed.
$\bigcup \mathcal {P} = 2^{\omega }$
as claimed.
Lemma 3.9.
![]() $\mathfrak {c} = \theta = \max (C)$
in
$\mathfrak {c} = \theta = \max (C)$
in
![]() $V^{\mathbb {P}_{\kappa }}$
.
$V^{\mathbb {P}_{\kappa }}$
.
Proof A straightforward transfinite induction on
![]() $\alpha $
shows that
$\alpha $
shows that
![]() $|\mathbb {P}_{\alpha }| = \theta $
for all
$|\mathbb {P}_{\alpha }| = \theta $
for all
![]() $\alpha \leq \kappa $
. (For the base case, clearly
$\alpha \leq \kappa $
. (For the base case, clearly
![]() $|\mathbb {P}_0| = \theta $
, and the limit case is also clear. For the successor case, suppose
$|\mathbb {P}_0| = \theta $
, and the limit case is also clear. For the successor case, suppose
![]() $|\mathbb {P}_{\alpha }| = \theta $
. Because
$|\mathbb {P}_{\alpha }| = \theta $
. Because
![]() $\mathbb {P}_{\alpha }$
has the ccc, there are
$\mathbb {P}_{\alpha }$
has the ccc, there are
![]() $\theta ^{\aleph _0} = \theta $
nice
$\theta ^{\aleph _0} = \theta $
nice
![]() $\mathbb {P}_{\alpha }$
-names for reals, and it follows that
$\mathbb {P}_{\alpha }$
-names for reals, and it follows that
![]() $|\mathbb {P}_{\alpha +1}| = \theta $
.) In particular,
$|\mathbb {P}_{\alpha +1}| = \theta $
.) In particular,
![]() $|\mathbb {P}_{\kappa }| = \theta $
, and because
$|\mathbb {P}_{\kappa }| = \theta $
, and because
![]() $\mathbb {P}_{\kappa }$
has the ccc, it follows that there are
$\mathbb {P}_{\kappa }$
has the ccc, it follows that there are
![]() $\theta ^{\aleph _0} = \theta $
nice
$\theta ^{\aleph _0} = \theta $
nice
![]() $\mathbb {P}_{\kappa }$
-names for reals. Hence
$\mathbb {P}_{\kappa }$
-names for reals. Hence
![]() $\mathfrak {c} \leq \theta $
in
$\mathfrak {c} \leq \theta $
in
![]() $V^{\mathbb {P}_{\kappa }}$
.
$V^{\mathbb {P}_{\kappa }}$
.
On the other hand, it is obvious that
![]() $\mathfrak {c} \geq \theta $
in
$\mathfrak {c} \geq \theta $
in
![]() $V^{\mathbb {P}_{\kappa }}$
, because of the Cohen reals added by
$V^{\mathbb {P}_{\kappa }}$
, because of the Cohen reals added by
![]() $\mathbb {P}_0$
.
$\mathbb {P}_0$
.
Lemma 3.10.
![]() $\mathrm {cov}(\mathcal M) = {\mathfrak d} = \acute {\mathfrak {n}} = \kappa = \min (C)$
in
$\mathrm {cov}(\mathcal M) = {\mathfrak d} = \acute {\mathfrak {n}} = \kappa = \min (C)$
in
![]() $V^{\mathbb {P}_{\kappa }}$
.
$V^{\mathbb {P}_{\kappa }}$
.
Proof By Lemma 3.8 and Corollary 2.6,
![]() $\kappa \geq \acute {\mathfrak {n}} \geq {\mathfrak d} \geq \mathrm {cov}(\mathcal M)$
in
$\kappa \geq \acute {\mathfrak {n}} \geq {\mathfrak d} \geq \mathrm {cov}(\mathcal M)$
in
![]() $V^{\mathbb {P}_{\kappa }}$
. So to prove the lemma, it suffices to show that
$V^{\mathbb {P}_{\kappa }}$
. So to prove the lemma, it suffices to show that
![]() $2^{\omega }$
cannot be covered with
$2^{\omega }$
cannot be covered with
![]() $<\!\kappa $
meager sets in
$<\!\kappa $
meager sets in
![]() $V^{\mathbb {P}_{\kappa }}$
.
$V^{\mathbb {P}_{\kappa }}$
.
Suppose
![]() $\lambda < \kappa $
and
$\lambda < \kappa $
and
![]() $\left \lbrace C_{\xi } \colon \xi < \lambda \right \rbrace $
is a collection of closed nowhere dense subsets of
$\left \lbrace C_{\xi } \colon \xi < \lambda \right \rbrace $
is a collection of closed nowhere dense subsets of
![]() $2^{\omega }$
in
$2^{\omega }$
in
![]() $V^{\mathbb {P}_{\kappa }}$
. For each
$V^{\mathbb {P}_{\kappa }}$
. For each
![]() $C_{\xi }$
, let
$C_{\xi }$
, let
![]() $A_{\xi }$
be a Borel code that evaluates to
$A_{\xi }$
be a Borel code that evaluates to
![]() $C_{\xi }$
. Because
$C_{\xi }$
. Because
![]() $\mathbb {P}_{\kappa }$
has the ccc and each
$\mathbb {P}_{\kappa }$
has the ccc and each
![]() $\mathbb {P}_{\alpha }$
is a complete sub-poset of
$\mathbb {P}_{\alpha }$
is a complete sub-poset of
![]() $\mathbb {P}_{\kappa }$
, there is for each
$\mathbb {P}_{\kappa }$
, there is for each
![]() $\xi $
some
$\xi $
some
![]() $\alpha < \kappa $
such that
$\alpha < \kappa $
such that
![]() $A_{\xi } \in V^{\mathbb {P}_{\alpha }}$
. Because
$A_{\xi } \in V^{\mathbb {P}_{\alpha }}$
. Because
![]() $\kappa $
is regular and
$\kappa $
is regular and
![]() $\lambda < \kappa $
, there is some particular
$\lambda < \kappa $
, there is some particular
![]() $\alpha < \kappa $
such that
$\alpha < \kappa $
such that
![]() $A_{\xi } \in V^{\mathbb {P}_{\alpha }}$
for all
$A_{\xi } \in V^{\mathbb {P}_{\alpha }}$
for all
![]() $\xi < \lambda $
. So to prove the lemma, it suffices to show that for each
$\xi < \lambda $
. So to prove the lemma, it suffices to show that for each
![]() $\alpha < \kappa $
there is some
$\alpha < \kappa $
there is some
![]() $c \in V^{\mathbb {P}_{\kappa }}$
not contained in any closed nowhere dense subset of
$c \in V^{\mathbb {P}_{\kappa }}$
not contained in any closed nowhere dense subset of
![]() $2^{\omega }$
coded in
$2^{\omega }$
coded in
![]() $V^{\mathbb {P}_{\alpha }}$
(i.e., we want c to be Cohen-generic over
$V^{\mathbb {P}_{\alpha }}$
(i.e., we want c to be Cohen-generic over
![]() $V^{\mathbb {P}_{\alpha }}$
).
$V^{\mathbb {P}_{\alpha }}$
).
Fix
![]() $\alpha < \kappa $
, and define
$\alpha < \kappa $
, and define
![]() $c: \omega \to 2$
by setting
$c: \omega \to 2$
by setting
We claim that c is Cohen-generic over
![]() $V^{\mathbb {P}_{\alpha }}$
. To see this, let
$V^{\mathbb {P}_{\alpha }}$
. To see this, let
![]() $U \subseteq 2^{\omega }$
be a dense open set whose Borel code is in
$U \subseteq 2^{\omega }$
be a dense open set whose Borel code is in
![]() $V^{\mathbb {P}_{\alpha }}$
. In particular,
$V^{\mathbb {P}_{\alpha }}$
. In particular,
![]() $\tilde U = \left \lbrace \tau \in 2^{<\omega } \colon [\![\tau ]\!] \subseteq U \right \rbrace \in V^{\mathbb {P}_{\alpha }}$
(where, abusing notation slightly,
$\tilde U = \left \lbrace \tau \in 2^{<\omega } \colon [\![\tau ]\!] \subseteq U \right \rbrace \in V^{\mathbb {P}_{\alpha }}$
(where, abusing notation slightly,
![]() $[\![\tau ]\!]$
denotes all those x in
$[\![\tau ]\!]$
denotes all those x in
![]() $2^{\omega }$
with
$2^{\omega }$
with
![]() $x \!\restriction \! \mathrm {dom}(\tau ) = \tau $
). Now fix
$x \!\restriction \! \mathrm {dom}(\tau ) = \tau $
). Now fix
![]() $p \in \mathbb {P}_{\kappa }$
. We will find an extension r of p forcing that
$p \in \mathbb {P}_{\kappa }$
. We will find an extension r of p forcing that
![]() $c \in U$
. Extending p if necessary, we may (and do) assume that there is some
$c \in U$
. Extending p if necessary, we may (and do) assume that there is some
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
![]() $(\alpha ,\mu ,n) \in \mathrm {dom}(p)$
for all
$(\alpha ,\mu ,n) \in \mathrm {dom}(p)$
for all
![]() $n < N$
, but
$n < N$
, but
![]() $(\alpha ,\mu ,n) \notin \mathrm {dom}(p)$
for all
$(\alpha ,\mu ,n) \notin \mathrm {dom}(p)$
for all
![]() $n \geq N$
. For all
$n \geq N$
. For all
![]() $n < N$
, let
$n < N$
, let
![]() $p(\alpha ,\mu ,n) = (t_n,B_n)$
. Define
$p(\alpha ,\mu ,n) = (t_n,B_n)$
. Define
![]() $\sigma \in 2^N$
by setting
$\sigma \in 2^N$
by setting
for all
![]() $n < N$
. Because U is dense in
$n < N$
. Because U is dense in
![]() $2^{\omega }$
, there is some
$2^{\omega }$
, there is some
![]() $\tau \in \tilde U$
such that
$\tau \in \tilde U$
such that
![]() $\tau \!\restriction \! N = \sigma $
. Because
$\tau \!\restriction \! N = \sigma $
. Because
![]() $\tilde U \in V^{\mathbb {P}_{\alpha }}$
, there is some
$\tilde U \in V^{\mathbb {P}_{\alpha }}$
, there is some
![]() $q \in \mathbb {P}_{\alpha }$
with
$q \in \mathbb {P}_{\alpha }$
with
![]() $q \leq _{\mathbb {P}_{\alpha }} p \!\restriction \! \alpha $
forcing that
$q \leq _{\mathbb {P}_{\alpha }} p \!\restriction \! \alpha $
forcing that
![]() $\tau \in \tilde U$
. Define
$\tau \in \tilde U$
. Define
![]() $r \in \mathbb {P}_{\kappa }$
by
$r \in \mathbb {P}_{\kappa }$
by
 $$ \begin{align*}r(j) = \begin{cases} r(j), & \text{if } j \in (I \times \omega) \cup (\alpha \times C \times \omega), \\ (\langle\tau(n)\rangle,\emptyset), & \text{if } j = (\alpha,\mu,n) \text{ for some } n \in \mathrm{dom}(\tau) \setminus \mathrm{dom}(\sigma), \\ p(j), & \text{otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}r(j) = \begin{cases} r(j), & \text{if } j \in (I \times \omega) \cup (\alpha \times C \times \omega), \\ (\langle\tau(n)\rangle,\emptyset), & \text{if } j = (\alpha,\mu,n) \text{ for some } n \in \mathrm{dom}(\tau) \setminus \mathrm{dom}(\sigma), \\ p(j), & \text{otherwise.} \end{cases}\end{align*} $$
Then
![]() $r \in \mathbb {P}_{\kappa }$
, and r forces
$r \in \mathbb {P}_{\kappa }$
, and r forces
![]() $c \in U$
. As U was an arbitrary open dense subset of
$c \in U$
. As U was an arbitrary open dense subset of
![]() $2^{\omega }$
coded in
$2^{\omega }$
coded in
![]() $V^{\mathbb {P}_{\alpha }}$
, this shows c is Cohen-generic over
$V^{\mathbb {P}_{\alpha }}$
, this shows c is Cohen-generic over
![]() $V^{\mathbb {P}_{\alpha }}$
.
$V^{\mathbb {P}_{\alpha }}$
.
From the last two lemmas, it follows that
![]() $\mathfrak {sp}({\small\text{closed}}) \subseteq [\kappa ,\theta ]$
in
$\mathfrak {sp}({\small\text{closed}}) \subseteq [\kappa ,\theta ]$
in
![]() $V^{\mathbb {P}_{\kappa }}$
, and if
$V^{\mathbb {P}_{\kappa }}$
, and if
![]() $\lambda> \theta $
then
$\lambda> \theta $
then
![]() $\lambda \notin \mathfrak {sp}({\small\text{Borel}})$
. To finish proving the theorem, it remains only to show that if
$\lambda \notin \mathfrak {sp}({\small\text{Borel}})$
. To finish proving the theorem, it remains only to show that if
![]() $\lambda \in [\kappa ,\theta ]$
and
$\lambda \in [\kappa ,\theta ]$
and
![]() $\lambda \notin C$
, then
$\lambda \notin C$
, then
![]() $\lambda \notin \mathfrak {sp}({\small\text{Borel}})$
. This is where the isomorphism-of-names argument comes in. This argument requires a rich supply of automorphisms of
$\lambda \notin \mathfrak {sp}({\small\text{Borel}})$
. This is where the isomorphism-of-names argument comes in. This argument requires a rich supply of automorphisms of
![]() $\mathbb {P}_{\kappa }$
, which we describe next.
$\mathbb {P}_{\kappa }$
, which we describe next.
If
![]() $\phi : I \to I$
is a permutation, then for every set x we define
$\phi : I \to I$
is a permutation, then for every set x we define
![]() $\bar \phi (x)$
to be the set obtained from x by replacing every
$\bar \phi (x)$
to be the set obtained from x by replacing every
![]() $i \in I$
in the transitive closure of x with
$i \in I$
in the transitive closure of x with
![]() $\phi (i)$
. This is well defined, because if
$\phi (i)$
. This is well defined, because if
![]() $i,j \in I$
then i is not in the transitive closure of j. (One may think of I as a set of urelements,
$i,j \in I$
then i is not in the transitive closure of j. (One may think of I as a set of urelements,
![]() $\phi $
as a permutation of them, and
$\phi $
as a permutation of them, and
![]() $\bar \phi $
as the automorphism of the universe induced by
$\bar \phi $
as the automorphism of the universe induced by
![]() $\phi $
.) Alternatively,
$\phi $
.) Alternatively,
![]() $\bar \phi $
is described via well-founded recursion by the relation
$\bar \phi $
is described via well-founded recursion by the relation
if
![]() $x \notin I$
, and
$x \notin I$
, and
![]() $\bar \phi \!\restriction \! I = \phi $
. In particular, if
$\bar \phi \!\restriction \! I = \phi $
. In particular, if
![]() $p \in \mathbb {P}_{\kappa }$
,
$p \in \mathbb {P}_{\kappa }$
,
![]() $\mathrm {dom}(\bar \phi (p)) = \bar \phi (\mathrm {dom}(p))$
and
$\mathrm {dom}(\bar \phi (p)) = \bar \phi (\mathrm {dom}(p))$
and
 $$ \begin{align*}\bar \phi(p)(j) = \begin{cases} p(i), & \text{if } i \in (I \times \omega) \cap \mathrm{dom}(p) \text{ and } \bar \phi(i) = j, \\ \big(t,\{ \bar \phi(\dot b) :\, \dot b \in B \}\big), & \text{if } j \in \mathrm{dom}(p) \setminus (I \times \omega) \text{ and } p(j) = (t,B), \end{cases}\end{align*} $$
$$ \begin{align*}\bar \phi(p)(j) = \begin{cases} p(i), & \text{if } i \in (I \times \omega) \cap \mathrm{dom}(p) \text{ and } \bar \phi(i) = j, \\ \big(t,\{ \bar \phi(\dot b) :\, \dot b \in B \}\big), & \text{if } j \in \mathrm{dom}(p) \setminus (I \times \omega) \text{ and } p(j) = (t,B), \end{cases}\end{align*} $$
and this expression can be taken as a recursive definition of
![]() $\bar \phi $
on
$\bar \phi $
on
![]() $\mathbb {P}_{\kappa }$
, and the natural extension of
$\mathbb {P}_{\kappa }$
, and the natural extension of
![]() $\bar \phi $
to the class of
$\bar \phi $
to the class of
![]() $\mathbb {P}_{\kappa }$
-names.
$\mathbb {P}_{\kappa }$
-names.
Lemma 3.11. Let
![]() $\phi $
be a permutation of I such that
$\phi $
be a permutation of I such that
![]() $\phi \!\restriction \! I_{\mu }$
is a permutation of
$\phi \!\restriction \! I_{\mu }$
is a permutation of
![]() $I_{\mu }$
for all
$I_{\mu }$
for all
![]() $\mu \in C$
. Then
$\mu \in C$
. Then
![]() $\bar \phi \!\restriction \! \mathbb {P}_{\alpha }$
is an automorphism of
$\bar \phi \!\restriction \! \mathbb {P}_{\alpha }$
is an automorphism of
![]() $\mathbb {P}_{\alpha }$
for all
$\mathbb {P}_{\alpha }$
for all
![]() $\alpha \leq \kappa $
.
$\alpha \leq \kappa $
.
Proof First, note that for all
![]() $p,q \in \mathbb {P}_{\alpha }$
, we have
$p,q \in \mathbb {P}_{\alpha }$
, we have
Together with the fact that
![]() $\bar \phi $
is invertible (with inverse
$\bar \phi $
is invertible (with inverse
![]() $\bar \phi ^{-1} = \overline {\phi ^{-1}}$
), this shows that the image of
$\bar \phi ^{-1} = \overline {\phi ^{-1}}$
), this shows that the image of
![]() $\mathbb {P}_{\alpha }$
under
$\mathbb {P}_{\alpha }$
under
![]() $\bar \phi $
is a poset, and is naturally isomorphic to
$\bar \phi $
is a poset, and is naturally isomorphic to
![]() $\mathbb {P}_{\alpha }$
as witnessed by
$\mathbb {P}_{\alpha }$
as witnessed by
![]() $\bar \phi $
. But it is not immediately clear that the image of
$\bar \phi $
. But it is not immediately clear that the image of
![]() $\mathbb {P}_{\alpha }$
under
$\mathbb {P}_{\alpha }$
under
![]() $\bar \phi $
is equal to
$\bar \phi $
is equal to
![]() $\mathbb {P}_{\alpha }$
, which is of course required for our claim that
$\mathbb {P}_{\alpha }$
, which is of course required for our claim that
![]() $\bar \phi \!\restriction \! \mathbb {P}_{\alpha }$
is an automorphism of
$\bar \phi \!\restriction \! \mathbb {P}_{\alpha }$
is an automorphism of
![]() $\mathbb {P}_{\alpha }$
. (In fact, one may show that this would not be true for
$\mathbb {P}_{\alpha }$
. (In fact, one may show that this would not be true for
![]() $\alpha \geq 1$
if
$\alpha \geq 1$
if
![]() $\phi $
were not required to fix all the
$\phi $
were not required to fix all the
![]() $I_{\mu }$
.) This is proved for
$I_{\mu }$
.) This is proved for
![]() $\bar \phi $
and its inverse, simultaneously, by induction on
$\bar \phi $
and its inverse, simultaneously, by induction on
![]() $\alpha $
.
$\alpha $
.
The base case
![]() $\alpha =0$
is clear. And for limit
$\alpha =0$
is clear. And for limit
![]() $\alpha $
, if
$\alpha $
, if
![]() $\bar \phi \!\restriction \! \mathbb {P}_{\xi }$
is an automorphism of
$\bar \phi \!\restriction \! \mathbb {P}_{\xi }$
is an automorphism of
![]() $\mathbb {P}_{\xi }$
, for all
$\mathbb {P}_{\xi }$
, for all
![]() $\xi < \alpha $
, then
$\xi < \alpha $
, then
![]() $\bar \phi \!\restriction \! \mathbb {P}_{\alpha }$
is an automorphism of
$\bar \phi \!\restriction \! \mathbb {P}_{\alpha }$
is an automorphism of
![]() $\mathbb {P}_{\alpha }$
because
$\mathbb {P}_{\alpha }$
because
![]() $\langle \mathbb {P}_{\alpha },\leq _{\mathbb {P}_{\alpha }} \rangle $
is the direct limit of
$\langle \mathbb {P}_{\alpha },\leq _{\mathbb {P}_{\alpha }} \rangle $
is the direct limit of
![]() $\left \langle \langle \mathbb {P}_{\xi },\leq _{\mathbb {P}_{\xi }} \rangle \colon \xi < \alpha \right \rangle $
. The same applies to
$\left \langle \langle \mathbb {P}_{\xi },\leq _{\mathbb {P}_{\xi }} \rangle \colon \xi < \alpha \right \rangle $
. The same applies to
![]() $\bar \phi ^{-1}$
.
$\bar \phi ^{-1}$
.
For the successor case, fix some
![]() $\beta < \kappa $
and suppose
$\beta < \kappa $
and suppose
![]() $\bar \phi \!\restriction \! \mathbb {P}_{\xi }$
is an automorphism of
$\bar \phi \!\restriction \! \mathbb {P}_{\xi }$
is an automorphism of
![]() $\mathbb {P}_{\xi }$
for all
$\mathbb {P}_{\xi }$
for all
![]() $\xi \leq \beta $
(the inductive hypothesis). Let
$\xi \leq \beta $
(the inductive hypothesis). Let
![]() $\alpha = \beta +1$
, and fix
$\alpha = \beta +1$
, and fix
![]() $p \in \mathbb {P}_{\alpha }$
. We claim that
$p \in \mathbb {P}_{\alpha }$
. We claim that
![]() $\bar \phi (p) \in \mathbb {P}_{\alpha }$
. Recall that
$\bar \phi (p) \in \mathbb {P}_{\alpha }$
. Recall that
 $$ \begin{align*}\bar \phi(p)(j) = \begin{cases} p(i), & \text{if } i \in (I \times \omega) \cap \mathrm{dom}(p) \text{ and } \bar \phi(i) = j, \\ \big(t,\{ \bar \phi(\dot b) :\, \dot b \in B \}\big), & \text{if } j \in \mathrm{dom}(p) \setminus (I \times \omega) \text{ and } p(j) = (t,B). \end{cases}\end{align*} $$
$$ \begin{align*}\bar \phi(p)(j) = \begin{cases} p(i), & \text{if } i \in (I \times \omega) \cap \mathrm{dom}(p) \text{ and } \bar \phi(i) = j, \\ \big(t,\{ \bar \phi(\dot b) :\, \dot b \in B \}\big), & \text{if } j \in \mathrm{dom}(p) \setminus (I \times \omega) \text{ and } p(j) = (t,B). \end{cases}\end{align*} $$
It is clear that
![]() $\bar \phi (p)$
is a finite partial function on
$\bar \phi (p)$
is a finite partial function on
![]() $(I \times \omega ) \cup (\alpha \times C \times \omega )$
, and that if
$(I \times \omega ) \cup (\alpha \times C \times \omega )$
, and that if
![]() $i \in (I \times \omega ) \cap \mathrm {dom}(\bar \phi (p))$
, then
$i \in (I \times \omega ) \cap \mathrm {dom}(\bar \phi (p))$
, then
![]() $\bar \phi (p)(i) = p(\phi ^{-1}(i)) \in \{0,1\}$
. It remains to check that the last bullet point in the definition of the conditions in
$\bar \phi (p)(i) = p(\phi ^{-1}(i)) \in \{0,1\}$
. It remains to check that the last bullet point in the definition of the conditions in
![]() $\mathbb {P}_{\alpha }$
is satisfied by
$\mathbb {P}_{\alpha }$
is satisfied by
![]() $\bar \phi (p)$
.
$\bar \phi (p)$
.
Suppose
![]() $(\gamma ,\mu ,n) \in \mathrm {dom}(\bar \phi (p))$
for some
$(\gamma ,\mu ,n) \in \mathrm {dom}(\bar \phi (p))$
for some
![]() $\gamma \leq \beta $
,
$\gamma \leq \beta $
,
![]() $\mu \in C$
, and
$\mu \in C$
, and
![]() $n \in \omega $
. This means
$n \in \omega $
. This means
![]() $(\gamma ,\mu ,n) \in \mathrm {dom}(p)$
as well: let us denote
$(\gamma ,\mu ,n) \in \mathrm {dom}(p)$
as well: let us denote
![]() $p(\gamma ,\mu ,n) = (t,B)$
. Then
$p(\gamma ,\mu ,n) = (t,B)$
. Then
Because
![]() $p \in \mathbb {P}_{\alpha }$
, t is a pruned subtree of
$p \in \mathbb {P}_{\alpha }$
, t is a pruned subtree of
![]() $2^{<k}$
for some
$2^{<k}$
for some
![]() $k \in \omega $
, and (by the inductive hypothesis, that
$k \in \omega $
, and (by the inductive hypothesis, that
![]() $\bar \phi \!\restriction \! \mathbb {P}_{\gamma }$
is an automorphism of
$\bar \phi \!\restriction \! \mathbb {P}_{\gamma }$
is an automorphism of
![]() $\mathbb {P}_{\gamma }$
),
$\mathbb {P}_{\gamma }$
),
![]() $\{ \bar \phi (\dot b) :\, \dot b \in B \}$
is a finite set of nice
$\{ \bar \phi (\dot b) :\, \dot b \in B \}$
is a finite set of nice
![]() $\mathbb {P}_{\gamma }$
-names for members of
$\mathbb {P}_{\gamma }$
-names for members of
![]() $2^{\omega }$
. Furthermore, by applying the automorphism
$2^{\omega }$
. Furthermore, by applying the automorphism
![]() $\bar \phi $
of
$\bar \phi $
of
![]() $\mathbb {P}_{\gamma }$
to the displayed statement in the last bullet point in the definition of the conditions in
$\mathbb {P}_{\gamma }$
to the displayed statement in the last bullet point in the definition of the conditions in
![]() $\mathbb {P}_{\alpha }$
, we get that for every
$\mathbb {P}_{\alpha }$
, we get that for every
![]() $\dot b \in B$
,
$\dot b \in B$
,
 $$ \begin{align*} \bar \phi(p) \restriction ((I \times \omega) \cup (\gamma \times C \times \omega)) \ \Vdash_{\mathbb{P}_{\gamma}} \quad & \bar \phi(\dot b) \!\restriction\! j \in t \text{ for every } j < k, \\ & \bar \phi(\dot b) \neq \bar \phi(\dot c_i) \text{ for every } i \in I_{\mu}, \text{ and} \\ & \bar \phi(\dot b) \text{ is not a branch of } \bar \phi(\dot T^{\xi}_{\mu,m}) \\ & \quad \text{ for any } \xi < \gamma \text{ and } m \in \omega. \end{align*} $$
$$ \begin{align*} \bar \phi(p) \restriction ((I \times \omega) \cup (\gamma \times C \times \omega)) \ \Vdash_{\mathbb{P}_{\gamma}} \quad & \bar \phi(\dot b) \!\restriction\! j \in t \text{ for every } j < k, \\ & \bar \phi(\dot b) \neq \bar \phi(\dot c_i) \text{ for every } i \in I_{\mu}, \text{ and} \\ & \bar \phi(\dot b) \text{ is not a branch of } \bar \phi(\dot T^{\xi}_{\mu,m}) \\ & \quad \text{ for any } \xi < \gamma \text{ and } m \in \omega. \end{align*} $$
Considering the second of these three statements, note that
![]() $\bar \phi (\dot c_i) = \dot c_{\phi (i)}$
for every
$\bar \phi (\dot c_i) = \dot c_{\phi (i)}$
for every
![]() $i \in I$
. Because
$i \in I$
. Because
![]() $\phi \!\restriction \! I_{\mu }$
is a permutation of
$\phi \!\restriction \! I_{\mu }$
is a permutation of
![]() $I_{\mu }$
, this means that the assertion “
$I_{\mu }$
, this means that the assertion “
![]() $\bar \phi (\dot b) \neq \bar \phi (\dot c_i) \text { for every } i \in I_{\mu }$
” is equivalent to the assertion “
$\bar \phi (\dot b) \neq \bar \phi (\dot c_i) \text { for every } i \in I_{\mu }$
” is equivalent to the assertion “
![]() $\bar \phi (\dot b) \neq \dot c_i \text { for every } i \in I_{\mu }$
.” Thus
$\bar \phi (\dot b) \neq \dot c_i \text { for every } i \in I_{\mu }$
.” Thus
Considering the third of these three statements, observe that
 $$ \begin{align*} \bar \phi(\dot T^{\xi}_{\mu,n}) &= \left\lbrace \bar \phi( \langle \sigma, p \rangle ) \colon p(\xi,\mu,m) = (t,B) \text{ for some } B \text{, and } \sigma \in t \right\rbrace \\ & = \left\lbrace \langle \sigma, \bar \phi(p) \rangle \colon p(\xi,\mu,m) = (t,B) \text{ for some } B \text{, and } \sigma \in t \right\rbrace \\ & = \left\lbrace \langle \sigma, \bar \phi(p) \rangle \colon \bar \phi(p)(\xi,\mu,m) = (t,\bar \phi(B)) \text{ for some } B \text{, and } \sigma \in t \right\rbrace \\ & = \left\lbrace \langle \sigma, \bar \phi(p) \rangle \colon \bar \phi(p)(\xi,\mu,m) = (t,B') \text{ for some } B' \text{, and } \sigma \in t \right\rbrace \\ & = \left\lbrace \langle \sigma, q \rangle \colon q(\xi,\mu,m) = (t,B') \text{ for some } B' \text{, and } \sigma \in t \right\rbrace \\ & = \dot T^{\xi}_{\mu,n}. \end{align*} $$
$$ \begin{align*} \bar \phi(\dot T^{\xi}_{\mu,n}) &= \left\lbrace \bar \phi( \langle \sigma, p \rangle ) \colon p(\xi,\mu,m) = (t,B) \text{ for some } B \text{, and } \sigma \in t \right\rbrace \\ & = \left\lbrace \langle \sigma, \bar \phi(p) \rangle \colon p(\xi,\mu,m) = (t,B) \text{ for some } B \text{, and } \sigma \in t \right\rbrace \\ & = \left\lbrace \langle \sigma, \bar \phi(p) \rangle \colon \bar \phi(p)(\xi,\mu,m) = (t,\bar \phi(B)) \text{ for some } B \text{, and } \sigma \in t \right\rbrace \\ & = \left\lbrace \langle \sigma, \bar \phi(p) \rangle \colon \bar \phi(p)(\xi,\mu,m) = (t,B') \text{ for some } B' \text{, and } \sigma \in t \right\rbrace \\ & = \left\lbrace \langle \sigma, q \rangle \colon q(\xi,\mu,m) = (t,B') \text{ for some } B' \text{, and } \sigma \in t \right\rbrace \\ & = \dot T^{\xi}_{\mu,n}. \end{align*} $$
The third equality is true because for any condition p,
![]() $p(\xi ,\mu ,m) = (t,B)$
if and only if
$p(\xi ,\mu ,m) = (t,B)$
if and only if
![]() $\bar \phi (p)(\xi ,\mu ,m) = (t,\bar \phi (B))$
. The fourth equality uses the inductive hypothesis, that
$\bar \phi (p)(\xi ,\mu ,m) = (t,\bar \phi (B))$
. The fourth equality uses the inductive hypothesis, that
![]() $\bar \phi \!\restriction \! \mathbb {P}_{\gamma }$
is an automorphism:
$\bar \phi \!\restriction \! \mathbb {P}_{\gamma }$
is an automorphism:
![]() $p(\xi ,\mu ,m) = (t,\bar \phi (B))$
for some B if and only if
$p(\xi ,\mu ,m) = (t,\bar \phi (B))$
for some B if and only if
![]() $p(\xi ,\mu ,m) = (t,B')$
for some
$p(\xi ,\mu ,m) = (t,B')$
for some
![]() $B'$
, specifically for
$B'$
, specifically for
![]() $B' = \bar \phi ^{-1}(B)$
. The fifth equality also uses the fact that
$B' = \bar \phi ^{-1}(B)$
. The fifth equality also uses the fact that
![]() $\bar \phi \!\restriction \! \mathbb {P}_{\gamma }$
is an automorphism. Thus
$\bar \phi \!\restriction \! \mathbb {P}_{\gamma }$
is an automorphism. Thus
 $$ \begin{align*} \bar \phi(p) \restriction ((I \times \omega) \cup (\gamma \times C \times \omega)) \ \Vdash_{\mathbb{P}_{\gamma}} \quad & \bar \phi(\dot b) \text{ is not a branch of } \dot T^{\xi}_{\mu,m} \\ & \quad \text{ for any } \xi < \gamma \text{ and } m \in \omega. \end{align*} $$
$$ \begin{align*} \bar \phi(p) \restriction ((I \times \omega) \cup (\gamma \times C \times \omega)) \ \Vdash_{\mathbb{P}_{\gamma}} \quad & \bar \phi(\dot b) \text{ is not a branch of } \dot T^{\xi}_{\mu,m} \\ & \quad \text{ for any } \xi < \gamma \text{ and } m \in \omega. \end{align*} $$
Putting these together, we obtain
 $$ \begin{align*} \bar \phi(p) \restriction ((I \times \omega) \cup (\gamma \times C \times \omega)) \ \Vdash_{\mathbb{P}_{\gamma}} \quad & \bar \phi(\dot b) \!\restriction\! j \in t \text{ for every } j < k, \\ & \bar \phi(\dot b) \neq c_i \text{ for every } i \in I_{\mu}, \text{ and} \\ & \bar \phi(\dot b) \text{ is not a branch of } \dot T^{\xi}_{\mu,m} \\ & \quad \text{ for any } \xi < \beta \text{ and } m \in \omega. \end{align*} $$
$$ \begin{align*} \bar \phi(p) \restriction ((I \times \omega) \cup (\gamma \times C \times \omega)) \ \Vdash_{\mathbb{P}_{\gamma}} \quad & \bar \phi(\dot b) \!\restriction\! j \in t \text{ for every } j < k, \\ & \bar \phi(\dot b) \neq c_i \text{ for every } i \in I_{\mu}, \text{ and} \\ & \bar \phi(\dot b) \text{ is not a branch of } \dot T^{\xi}_{\mu,m} \\ & \quad \text{ for any } \xi < \beta \text{ and } m \in \omega. \end{align*} $$
In other words,
![]() $\bar \phi (p)$
satisfies the final bullet point in the definition of the
$\bar \phi (p)$
satisfies the final bullet point in the definition of the
![]() $\mathbb {P}_{\alpha }$
conditions. Hence
$\mathbb {P}_{\alpha }$
conditions. Hence
![]() $\bar \phi (p) \in \mathbb {P}_{\alpha }$
, as claimed.
$\bar \phi (p) \in \mathbb {P}_{\alpha }$
, as claimed.
This shows that (the restriction of)
![]() $\bar \phi $
is an injective morphism from
$\bar \phi $
is an injective morphism from
![]() $\mathbb {P}_{\alpha }$
to
$\mathbb {P}_{\alpha }$
to
![]() $\mathbb {P}_{\alpha }$
. To get surjectivity, simply note that the same argument applies to
$\mathbb {P}_{\alpha }$
. To get surjectivity, simply note that the same argument applies to
![]() $\bar \phi ^{-1} = \overline {\phi ^{-1}}$
as well.
$\bar \phi ^{-1} = \overline {\phi ^{-1}}$
as well.
From now on, we work in the ground model. Let
![]() $\lambda $
be a cardinal such that
$\lambda $
be a cardinal such that
![]() $\lambda \in [\kappa ,\theta ]$
and
$\lambda \in [\kappa ,\theta ]$
and
![]() $\lambda \notin C$
. Suppose
$\lambda \notin C$
. Suppose
![]() $\big \{ \dot B_{\alpha } :\, \alpha < \lambda \big \}$
is a set of nice
$\big \{ \dot B_{\alpha } :\, \alpha < \lambda \big \}$
is a set of nice
![]() $\mathbb {P}_{\kappa }$
-names for Borel codes for subsets of
$\mathbb {P}_{\kappa }$
-names for Borel codes for subsets of
![]() $\mathbb {R}$
. (Any standard method of constructing Borel codes can be used for the proof, provided only that the codes are hereditarily countable sets. But for concreteness, let us take a Borel code to be a subset of
$\mathbb {R}$
. (Any standard method of constructing Borel codes can be used for the proof, provided only that the codes are hereditarily countable sets. But for concreteness, let us take a Borel code to be a subset of
![]() $\omega $
.) We let
$\omega $
.) We let
![]() $B_{\alpha } \subseteq \omega $
denote the evaluation of the name
$B_{\alpha } \subseteq \omega $
denote the evaluation of the name
![]() $\dot B_{\alpha }$
in
$\dot B_{\alpha }$
in
![]() $V^{\mathbb {P}_{\kappa }}$
, and we let
$V^{\mathbb {P}_{\kappa }}$
, and we let
![]() $\tilde B_{\alpha } \subseteq \mathbb {R}$
denote the interpretation of
$\tilde B_{\alpha } \subseteq \mathbb {R}$
denote the interpretation of
![]() $B_{\alpha }$
.
$B_{\alpha }$
.
We aim to show that
![]() $\big \{ \tilde B_{\alpha } :\, \alpha < \lambda \big \}$
is not a partition of
$\big \{ \tilde B_{\alpha } :\, \alpha < \lambda \big \}$
is not a partition of
![]() $\mathbb {R}$
in
$\mathbb {R}$
in
![]() $V^{\mathbb {P}_{\kappa }}$
. To this end, suppose
$V^{\mathbb {P}_{\kappa }}$
. To this end, suppose
![]() $q \in \mathbb {P}_{\kappa }$
and q forces each of the
$q \in \mathbb {P}_{\kappa }$
and q forces each of the
![]() $\tilde B_{\alpha }$
is nonempty, and
$\tilde B_{\alpha }$
is nonempty, and
![]() $\tilde B_{\alpha } \cap \tilde B_{\beta } = \emptyset $
whenever
$\tilde B_{\alpha } \cap \tilde B_{\beta } = \emptyset $
whenever
![]() $\alpha \neq \beta $
. We will show that q also forces
$\alpha \neq \beta $
. We will show that q also forces
![]() $\bigcup _{\alpha < \lambda } \tilde B_{\alpha } \neq \mathbb {R}$
.
$\bigcup _{\alpha < \lambda } \tilde B_{\alpha } \neq \mathbb {R}$
.
Fix a cardinal
![]() $\nu \leq \lambda $
such that
$\nu \leq \lambda $
such that
![]() $\alpha ^{\aleph _0} < \nu $
for all cardinals
$\alpha ^{\aleph _0} < \nu $
for all cardinals
![]() $\alpha < \nu $
, and such that C contains no cardinals in the interval
$\alpha < \nu $
, and such that C contains no cardinals in the interval
![]() $[\nu ,\lambda ]$
. If
$[\nu ,\lambda ]$
. If
![]() $\lambda $
is neither singular nor the successor of a singular cardinal, then we may simply take
$\lambda $
is neither singular nor the successor of a singular cardinal, then we may simply take
![]() $\lambda = \nu $
. Otherwise, using the last two bullet points in our description of C, there is an infinite interval of cardinals below
$\lambda = \nu $
. Otherwise, using the last two bullet points in our description of C, there is an infinite interval of cardinals below
![]() $\lambda $
and disjoint from C, and we may take
$\lambda $
and disjoint from C, and we may take
![]() $\nu $
to be any successor-of-a-successor cardinal in this interval. In either case,
$\nu $
to be any successor-of-a-successor cardinal in this interval. In either case,
![]() $\alpha ^{\aleph _0} < \nu $
for all cardinals
$\alpha ^{\aleph _0} < \nu $
for all cardinals
![]() $\alpha < \nu $
by the
$\alpha < \nu $
by the
![]() $\mathsf {GCH}$
.
$\mathsf {GCH}$
.
Given
![]() $\alpha \leq \kappa $
and a condition
$\alpha \leq \kappa $
and a condition
![]() $p \in \mathbb {P}_{\alpha }$
, for each
$p \in \mathbb {P}_{\alpha }$
, for each
![]() $\mu \in C$
define
$\mu \in C$
define
where
![]() $\text {TC}(p)$
denotes the transitive closure of p. We think of
$\text {TC}(p)$
denotes the transitive closure of p. We think of
![]() $\mathrm {hdom}_{\mu }(p)$
as the “hereditary domain” of p on
$\mathrm {hdom}_{\mu }(p)$
as the “hereditary domain” of p on
![]() $I_{\mu }$
: all those
$I_{\mu }$
: all those
![]() $i \in I_{\mu }$
that are used at any stage in building the condition p. A straightforward transfinite induction on
$i \in I_{\mu }$
that are used at any stage in building the condition p. A straightforward transfinite induction on
![]() $\alpha $
shows that
$\alpha $
shows that
![]() $\left \lvert \mathrm {hdom}_{\mu }(p) \right \rvert \leq \aleph _0$
for every
$\left \lvert \mathrm {hdom}_{\mu }(p) \right \rvert \leq \aleph _0$
for every
![]() $p \in \mathbb {P}_{\alpha }$
and every
$p \in \mathbb {P}_{\alpha }$
and every
![]() $\mu \in C$
. (The base case and the limit case are clear. For the successor case, use the fact that
$\mu \in C$
. (The base case and the limit case are clear. For the successor case, use the fact that
![]() $\mathbb {P}_{\alpha }$
has the ccc.) Similarly, for each
$\mathbb {P}_{\alpha }$
has the ccc.) Similarly, for each
![]() $\mathbb {P}_{\kappa }$
-name
$\mathbb {P}_{\kappa }$
-name
![]() $\dot x$
and each
$\dot x$
and each
![]() $\mu \in C$
, let
$\mu \in C$
, let
![]() $\mathrm {hdom}_{\mu }(\dot x) = \textstyle \text {TC}(\dot x) \cap I_{\mu }$
. As before, it is not difficult to see that if
$\mathrm {hdom}_{\mu }(\dot x) = \textstyle \text {TC}(\dot x) \cap I_{\mu }$
. As before, it is not difficult to see that if
![]() $\dot x$
is a nice
$\dot x$
is a nice
![]() $\mathbb {P}_{\kappa }$
-name for a Borel code (or for any hereditarily countable set), then
$\mathbb {P}_{\kappa }$
-name for a Borel code (or for any hereditarily countable set), then
![]() $\mathrm {hdom}_{\mu }(\dot x)$
is countable for every
$\mathrm {hdom}_{\mu }(\dot x)$
is countable for every
![]() $\mu \in C$
.
$\mu \in C$
.
For each
![]() $\alpha < \lambda $
and each
$\alpha < \lambda $
and each
![]() $\mu \in C$
, let
$\mu \in C$
, let
![]() $D^{\alpha }_{\mu } = \mathrm {hdom}_{\mu }(\dot B_{\alpha }).$
Note that
$D^{\alpha }_{\mu } = \mathrm {hdom}_{\mu }(\dot B_{\alpha }).$
Note that
![]() $D^{\alpha }_{\mu }$
is countable for each
$D^{\alpha }_{\mu }$
is countable for each
![]() $\alpha < \lambda $
and
$\alpha < \lambda $
and
![]() $\mu \in C$
. Expanding some of the
$\mu \in C$
. Expanding some of the
![]() $D^{\alpha }_{\mu }$
if necessary, we may (and do) assume each
$D^{\alpha }_{\mu }$
if necessary, we may (and do) assume each
![]() $D^{\alpha }_{\mu }$
is countably infinite and includes
$D^{\alpha }_{\mu }$
is countably infinite and includes
![]() $\mathrm {hdom}_{\mu }(q)$
. For each
$\mathrm {hdom}_{\mu }(q)$
. For each
![]() $\alpha < \lambda $
, let
$\alpha < \lambda $
, let
![]() $D^{\alpha } = \bigcup _{\mu \in C}D^{\alpha }_{\mu }$
. We note that
$D^{\alpha } = \bigcup _{\mu \in C}D^{\alpha }_{\mu }$
. We note that
![]() $|D^{\alpha }| = \sum _{\mu \in C}|D^{\alpha }_{\mu }| = |C| \cdot \aleph _0$
for all
$|D^{\alpha }| = \sum _{\mu \in C}|D^{\alpha }_{\mu }| = |C| \cdot \aleph _0$
for all
![]() $\alpha < \lambda $
, and
$\alpha < \lambda $
, and
![]() $|C| \cdot \aleph _0 < \min (C) = \kappa $
. (Note: the inequality
$|C| \cdot \aleph _0 < \min (C) = \kappa $
. (Note: the inequality
![]() $|C| \cdot \aleph _0 < \min (C)$
uses the second bullet point in our description of C.)
$|C| \cdot \aleph _0 < \min (C)$
uses the second bullet point in our description of C.)
By our choice of
![]() $\nu $
, together with the aforementioned fact that
$\nu $
, together with the aforementioned fact that
![]() $|D^{\alpha }| < \kappa $
for all
$|D^{\alpha }| < \kappa $
for all
![]() $\alpha < \lambda $
,
$\alpha < \lambda $
,
![]() $\left \lbrace D^{\alpha } \colon \alpha < \nu \right \rbrace $
meets the conditions of the generalized
$\left \lbrace D^{\alpha } \colon \alpha < \nu \right \rbrace $
meets the conditions of the generalized
![]() $\Delta $
-system lemma [Reference Kunen15, Lemma III.6.15]. Thus there is some
$\Delta $
-system lemma [Reference Kunen15, Lemma III.6.15]. Thus there is some
![]() $\mathcal {A}_0 \subseteq \nu $
with
$\mathcal {A}_0 \subseteq \nu $
with
![]() $\left \lvert \mathcal {A}_0 \right \rvert = \nu $
such that
$\left \lvert \mathcal {A}_0 \right \rvert = \nu $
such that
![]() $\left \lbrace D^{\alpha } \colon \alpha \in \mathcal {A}_0 \right \rbrace $
is a
$\left \lbrace D^{\alpha } \colon \alpha \in \mathcal {A}_0 \right \rbrace $
is a
![]() $\Delta $
-system with root R.
$\Delta $
-system with root R.
Let
![]() $\mathcal {A}_1 = \left \lbrace \alpha \in \mathcal {A}_0 \colon D^{\alpha }_{\mu } \setminus R = \emptyset \text { for all } \mu \in C \text { with } \mu < \lambda \right \rbrace $
. For all
$\mathcal {A}_1 = \left \lbrace \alpha \in \mathcal {A}_0 \colon D^{\alpha }_{\mu } \setminus R = \emptyset \text { for all } \mu \in C \text { with } \mu < \lambda \right \rbrace $
. For all
![]() $\mu \in C$
,
$\mu \in C$
,
![]() $\left \lbrace D^{\alpha }_{\mu } \setminus R \colon \alpha \in \mathcal {A}_0 \right \rbrace $
is a
$\left \lbrace D^{\alpha }_{\mu } \setminus R \colon \alpha \in \mathcal {A}_0 \right \rbrace $
is a
![]() $\nu $
-size collection of pairwise disjoint subsets of
$\nu $
-size collection of pairwise disjoint subsets of
![]() $I_{\mu }$
. If also
$I_{\mu }$
. If also
![]() $\mu < \lambda $
, then
$\mu < \lambda $
, then
![]() $\mu < \nu $
and it follows that
$\mu < \nu $
and it follows that
![]() $D^{\alpha }_{\mu } \setminus R = \emptyset $
for all but (at most)
$D^{\alpha }_{\mu } \setminus R = \emptyset $
for all but (at most)
![]() $\mu $
members of
$\mu $
members of
![]() $\mathcal {A}_0$
. Furthermore,
$\mathcal {A}_0$
. Furthermore,
![]() $|\left \lbrace \mu \in C \colon \mu < \lambda \right \rbrace | \leq |C| < \kappa < \nu $
. It follows that
$|\left \lbrace \mu \in C \colon \mu < \lambda \right \rbrace | \leq |C| < \kappa < \nu $
. It follows that
![]() $\left \lvert \mathcal {A}_1 \right \rvert = \nu $
.
$\left \lvert \mathcal {A}_1 \right \rvert = \nu $
.
For each
![]() $\alpha < \lambda $
and
$\alpha < \lambda $
and
![]() $\mu \in C$
, fix a bijection
$\mu \in C$
, fix a bijection
![]() $\phi ^{\alpha }_{\mu }: D^{\alpha }_{\mu } \to \omega $
, in such a way that
$\phi ^{\alpha }_{\mu }: D^{\alpha }_{\mu } \to \omega $
, in such a way that
![]() $\phi ^{\alpha }_{\mu } \!\restriction \! R = \phi ^{\beta }_{\mu } \!\restriction \! R$
for all
$\phi ^{\alpha }_{\mu } \!\restriction \! R = \phi ^{\beta }_{\mu } \!\restriction \! R$
for all
![]() $\alpha ,\beta < \lambda $
. For each
$\alpha ,\beta < \lambda $
. For each
![]() $\alpha ,\beta < \lambda $
and
$\alpha ,\beta < \lambda $
and
![]() $\mu \in C$
, let
$\mu \in C$
, let
![]() $\phi ^{\alpha ,\beta }_{\mu }$
be the involution of
$\phi ^{\alpha ,\beta }_{\mu }$
be the involution of
![]() $I_{\mu }$
given by
$I_{\mu }$
given by
 $$ \begin{align*}\phi^{\alpha,\beta}_{\mu}(i) = \begin{cases} (\phi^{\beta}_{\mu})^{-1} \circ \phi^{\alpha}_{\mu}(i), \quad & \text{if } i \in D^{\alpha}_{\mu}, \\ (\phi^{\alpha}_{\mu})^{-1} \circ \phi^{\beta}_{\mu}(i), & \text{if } i \in D^{\beta}_{\mu}, \\ i, &\text{otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}\phi^{\alpha,\beta}_{\mu}(i) = \begin{cases} (\phi^{\beta}_{\mu})^{-1} \circ \phi^{\alpha}_{\mu}(i), \quad & \text{if } i \in D^{\alpha}_{\mu}, \\ (\phi^{\alpha}_{\mu})^{-1} \circ \phi^{\beta}_{\mu}(i), & \text{if } i \in D^{\beta}_{\mu}, \\ i, &\text{otherwise.} \end{cases}\end{align*} $$
(Recall that an “involution” of a set S means a bijection
![]() $f: S \to S$
such that
$f: S \to S$
such that
![]() $\psi \circ \psi = \mathrm {id}_S$
.) This function is well defined, because
$\psi \circ \psi = \mathrm {id}_S$
.) This function is well defined, because
![]() $D^{\alpha }_{\mu } \cap D^{\beta }_{\mu } = R$
, and
$D^{\alpha }_{\mu } \cap D^{\beta }_{\mu } = R$
, and
![]() $(\phi ^{\beta }_{\mu })^{-1} \circ \phi ^{\alpha }_{\mu }(i) = i = (\phi ^{\alpha }_{\mu })^{-1} \circ \phi ^{\beta }_{\mu }(i)$
whenever
$(\phi ^{\beta }_{\mu })^{-1} \circ \phi ^{\alpha }_{\mu }(i) = i = (\phi ^{\alpha }_{\mu })^{-1} \circ \phi ^{\beta }_{\mu }(i)$
whenever
![]() $i \in R$
. This gives us a collection
$i \in R$
. This gives us a collection
![]() $\left \lbrace \phi ^{\alpha ,\beta }_{\mu } \colon \alpha ,\beta < \lambda \right \rbrace $
of involutions of
$\left \lbrace \phi ^{\alpha ,\beta }_{\mu } \colon \alpha ,\beta < \lambda \right \rbrace $
of involutions of
![]() $I_{\mu }$
such that for any
$I_{\mu }$
such that for any
![]() $\alpha ,\beta < \lambda $
,
$\alpha ,\beta < \lambda $
,
-
∘
 $\phi ^{\alpha ,\beta }_{\mu }$
maps
$\phi ^{\alpha ,\beta }_{\mu }$
maps
 $D^{\alpha }_{\mu }$
onto
$D^{\alpha }_{\mu }$
onto
 $D^{\beta }_{\mu }$
and
$D^{\beta }_{\mu }$
and
 $D^{\beta }_{\mu }$
onto
$D^{\beta }_{\mu }$
onto
 $D^{\alpha }_{\mu }$
, but acts as the identity on the rest of
$D^{\alpha }_{\mu }$
, but acts as the identity on the rest of
 $I_{\mu }$
,
$I_{\mu }$
, -
∘
 $\phi ^{\alpha ,\beta }_{\mu }$
acts as the identity on
$\phi ^{\alpha ,\beta }_{\mu }$
acts as the identity on
 $R \cap I_{\mu }$
, and
$R \cap I_{\mu }$
, and -
∘
 $\phi ^{\alpha ,\beta }_{\mu } = \phi ^{\gamma ,\beta }_{\mu } \circ \phi ^{\alpha ,\gamma }_{\mu }$
for any
$\phi ^{\alpha ,\beta }_{\mu } = \phi ^{\gamma ,\beta }_{\mu } \circ \phi ^{\alpha ,\gamma }_{\mu }$
for any
 $\gamma < \lambda $
.
$\gamma < \lambda $
.
For each
![]() $\alpha ,\beta < \lambda $
, let
$\alpha ,\beta < \lambda $
, let
![]() $\phi ^{\alpha ,\beta }$
denote the product map
$\phi ^{\alpha ,\beta }$
denote the product map
![]() $\bigotimes _{\mu \in C}\phi ^{\alpha ,\beta }_{\mu }$
(that is, the map defined by setting
$\bigotimes _{\mu \in C}\phi ^{\alpha ,\beta }_{\mu }$
(that is, the map defined by setting
![]() $\phi ^{\alpha ,\beta }(i) = \phi ^{\alpha ,\beta }_{\mu }(i)$
whenever
$\phi ^{\alpha ,\beta }(i) = \phi ^{\alpha ,\beta }_{\mu }(i)$
whenever
![]() $i \in I_{\mu }$
). This is an involution of I, and restricts to
$i \in I_{\mu }$
). This is an involution of I, and restricts to
![]() $\phi ^{\alpha ,\beta }_{\mu }$
on each
$\phi ^{\alpha ,\beta }_{\mu }$
on each
![]() $I_{\mu }$
. In particular, Lemma 3.11 applies, and
$I_{\mu }$
. In particular, Lemma 3.11 applies, and
![]() $\bar \phi ^{\alpha ,\beta } \!\restriction \! \mathbb {P}_{\kappa }$
is an automorphism of
$\bar \phi ^{\alpha ,\beta } \!\restriction \! \mathbb {P}_{\kappa }$
is an automorphism of
![]() $\mathbb {P}_{\kappa }$
for each
$\mathbb {P}_{\kappa }$
for each
![]() $\alpha ,\beta < \lambda $
.
$\alpha ,\beta < \lambda $
.
Lemma 3.12. There are at most
![]() $\kappa $
nice
$\kappa $
nice
![]() $\mathbb {P}_{\kappa }$
-names
$\mathbb {P}_{\kappa }$
-names
![]() $\dot x$
for subsets of
$\dot x$
for subsets of
![]() $\omega $
with the property that
$\omega $
with the property that
![]() $\mathrm {hdom}(\dot x) \subseteq D^0$
.
$\mathrm {hdom}(\dot x) \subseteq D^0$
.
Proof For each
![]() $\alpha \leq \kappa $
, let
$\alpha \leq \kappa $
, let
![]() $\mathbb {P}_{\alpha } \!\restriction \! D^0 = \left \lbrace p \in \mathbb {P}_{\alpha } \colon \mathrm {hdom}(p) \subseteq D^0 \right \rbrace $
. We prove by transfinite induction on
$\mathbb {P}_{\alpha } \!\restriction \! D^0 = \left \lbrace p \in \mathbb {P}_{\alpha } \colon \mathrm {hdom}(p) \subseteq D^0 \right \rbrace $
. We prove by transfinite induction on
![]() $\alpha $
that for all
$\alpha $
that for all
![]() $\alpha \leq \kappa $
,
$\alpha \leq \kappa $
,
![]() $\left \lvert \mathbb {P}_{\alpha } \!\restriction \! D^0 \right \rvert \leq \kappa $
and there are
$\left \lvert \mathbb {P}_{\alpha } \!\restriction \! D^0 \right \rvert \leq \kappa $
and there are
![]() $\leq \! \kappa $
nice
$\leq \! \kappa $
nice
![]() $\mathbb {P}_{\alpha } \!\restriction \! D^0$
-names for subsets of
$\mathbb {P}_{\alpha } \!\restriction \! D^0$
-names for subsets of
![]() $\omega $
. Note that a nice
$\omega $
. Note that a nice
![]() $\mathbb {P}_{\alpha } \!\restriction \! D^0$
-name for a subset of
$\mathbb {P}_{\alpha } \!\restriction \! D^0$
-name for a subset of
![]() $\omega $
is the same thing as a nice
$\omega $
is the same thing as a nice
![]() $\mathbb {P}_{\alpha }$
-name
$\mathbb {P}_{\alpha }$
-name
![]() $\dot x$
for a subset of
$\dot x$
for a subset of
![]() $\omega $
with the property that
$\omega $
with the property that
![]() $\mathrm {hdom}(\dot x) \subseteq D^0$
.
$\mathrm {hdom}(\dot x) \subseteq D^0$
.
For the base case,
![]() $\mathbb {P}_0 \!\restriction \! D^0$
is just the set of finite partial functions
$\mathbb {P}_0 \!\restriction \! D^0$
is just the set of finite partial functions
![]() $D^0 \to 2$
, so
$D^0 \to 2$
, so
![]() $\left \lvert \mathbb {P}_{\alpha } \!\restriction \! D^0 \right \rvert = \aleph _0 \leq \kappa $
because
$\left \lvert \mathbb {P}_{\alpha } \!\restriction \! D^0 \right \rvert = \aleph _0 \leq \kappa $
because
![]() $D^0$
is countable. Because
$D^0$
is countable. Because
![]() $\mathbb {P}_0 \!\restriction \! D^0$
has the ccc, there are
$\mathbb {P}_0 \!\restriction \! D^0$
has the ccc, there are
![]() $\aleph _0$
nice
$\aleph _0$
nice
![]() $\mathbb {P}_0 \!\restriction \! D^0$
-names for subsets of
$\mathbb {P}_0 \!\restriction \! D^0$
-names for subsets of
![]() $\omega $
.
$\omega $
.
For the other cases, fix
![]() $\alpha \leq \kappa $
, and suppose
$\alpha \leq \kappa $
, and suppose
![]() $\left \lvert \mathbb {P}_{\xi } \!\restriction \! D^0 \right \rvert \leq \kappa $
and there are
$\left \lvert \mathbb {P}_{\xi } \!\restriction \! D^0 \right \rvert \leq \kappa $
and there are
![]() $\leq \! \kappa $
nice
$\leq \! \kappa $
nice
![]() $\mathbb {P}_{\xi } \!\restriction \! D^0$
-names for subsets of
$\mathbb {P}_{\xi } \!\restriction \! D^0$
-names for subsets of
![]() $\omega $
, for all
$\omega $
, for all
![]() $\xi < \alpha $
. A condition in
$\xi < \alpha $
. A condition in
![]() $\mathbb {P}^{\alpha } \!\restriction \! D^0$
is defined in the same way as a condition in
$\mathbb {P}^{\alpha } \!\restriction \! D^0$
is defined in the same way as a condition in
![]() $\mathbb {P}^{\alpha }$
, except that we restrict the
$\mathbb {P}^{\alpha }$
, except that we restrict the
![]() $\dot b$
in that definition to members of
$\dot b$
in that definition to members of
![]() $\mathbb {P}_{\gamma } \!\restriction \! D^0$
. Using the inductive hypothesis on
$\mathbb {P}_{\gamma } \!\restriction \! D^0$
. Using the inductive hypothesis on
![]() $\mathbb {P}_{\gamma } \!\restriction \! D^0$
-names, it follows that
$\mathbb {P}_{\gamma } \!\restriction \! D^0$
-names, it follows that
![]() $\left \lvert \mathbb {P}_{\alpha } \!\restriction \! D^0 \right \rvert \leq \kappa $
. Each nice
$\left \lvert \mathbb {P}_{\alpha } \!\restriction \! D^0 \right \rvert \leq \kappa $
. Each nice
![]() $\mathbb {P}_{\alpha } \!\restriction \! D^0$
-name
$\mathbb {P}_{\alpha } \!\restriction \! D^0$
-name
![]() $\dot x$
for a subset of
$\dot x$
for a subset of
![]() $\omega $
has the form
$\omega $
has the form
![]() $\dot x = \left \lbrace \langle n,p \rangle \colon p \in \mathcal {A}_n \right \rbrace $
, where each
$\dot x = \left \lbrace \langle n,p \rangle \colon p \in \mathcal {A}_n \right \rbrace $
, where each
![]() $\mathcal {A}_n$
is an antichain in
$\mathcal {A}_n$
is an antichain in
![]() $\mathbb {P}_{\alpha } \!\restriction \! D^0$
. Because
$\mathbb {P}_{\alpha } \!\restriction \! D^0$
. Because
![]() $\mathbb {P}_{\alpha }$
has the ccc, each
$\mathbb {P}_{\alpha }$
has the ccc, each
![]() $\mathcal {A}_n$
is countable. Thus there are
$\mathcal {A}_n$
is countable. Thus there are
![]() $\kappa ^{\aleph _0} = \kappa $
names
$\kappa ^{\aleph _0} = \kappa $
names
![]() $\dot x$
with this form.
$\dot x$
with this form.
In particular, there are
![]() $\kappa $
nice
$\kappa $
nice
![]() $\mathbb {P}_{\kappa }$
-names
$\mathbb {P}_{\kappa }$
-names
![]() $\dot x$
for subsets of
$\dot x$
for subsets of
![]() $\omega $
having the property that
$\omega $
having the property that
![]() $\mathrm {hdom}(\dot x) \subseteq D^0$
. But for each
$\mathrm {hdom}(\dot x) \subseteq D^0$
. But for each
![]() $\alpha \in \mathcal {A}_1$
,
$\alpha \in \mathcal {A}_1$
,
![]() $\bar \phi ^{\alpha ,0}(\dot B_{\alpha })$
is just such a name. By the pigeonhole principle, and the fact that
$\bar \phi ^{\alpha ,0}(\dot B_{\alpha })$
is just such a name. By the pigeonhole principle, and the fact that
![]() $\kappa < \nu $
, this implies that there is some
$\kappa < \nu $
, this implies that there is some
![]() $\mathcal {A}_2 \subseteq \mathcal {A}_1$
with
$\mathcal {A}_2 \subseteq \mathcal {A}_1$
with
![]() $\left \lvert \mathcal {A}_2 \right \rvert = \nu $
such that
$\left \lvert \mathcal {A}_2 \right \rvert = \nu $
such that
![]() $\bar \phi ^{\alpha ,0}(\dot B_{\alpha }) = \bar \phi ^{\beta ,0}(\dot B_{\beta })$
whenever
$\bar \phi ^{\alpha ,0}(\dot B_{\alpha }) = \bar \phi ^{\beta ,0}(\dot B_{\beta })$
whenever
![]() $\alpha ,\beta \in \mathcal {A}_2$
. Reindexing the
$\alpha ,\beta \in \mathcal {A}_2$
. Reindexing the
![]() $\dot B_{\alpha }$
’s if necessary, we may (and do) assume
$\dot B_{\alpha }$
’s if necessary, we may (and do) assume
![]() $0 \in \mathcal {A}_2$
.
$0 \in \mathcal {A}_2$
.
We now proceed to define a new
![]() $\mathbb {P}_{\kappa }$
-name
$\mathbb {P}_{\kappa }$
-name
![]() $\dot B_{\lambda }$
for a subset of
$\dot B_{\lambda }$
for a subset of
![]() $\omega $
.
$\omega $
.
First, for all
![]() $\mu \in C$
with
$\mu \in C$
with
![]() $\mu < \lambda $
, let
$\mu < \lambda $
, let
![]() $D^{\lambda }_{\mu } = R \cap I_{\mu }$
. (Recall that
$D^{\lambda }_{\mu } = R \cap I_{\mu }$
. (Recall that
![]() $D^{\alpha }_{\mu } \cap I_{\mu } \subseteq R$
whenever
$D^{\alpha }_{\mu } \cap I_{\mu } \subseteq R$
whenever
![]() $\mu \in C$
and
$\mu \in C$
and
![]() $\mu < \lambda $
and
$\mu < \lambda $
and
![]() $\alpha \in \mathcal {A}_1$
. Thus, in this case,
$\alpha \in \mathcal {A}_1$
. Thus, in this case,
![]() $D^{\lambda }_{\mu } \cap D^{\alpha }_{\mu } = R \cap I_{\mu }$
for all
$D^{\lambda }_{\mu } \cap D^{\alpha }_{\mu } = R \cap I_{\mu }$
for all
![]() $\alpha \in \mathcal {A}_1 \supseteq \mathcal {A}_2$
.) Next, for each
$\alpha \in \mathcal {A}_1 \supseteq \mathcal {A}_2$
.) Next, for each
![]() $\mu \in C$
with
$\mu \in C$
with
![]() $\mu> \lambda $
, let
$\mu> \lambda $
, let
![]() $D^{\lambda }_{\mu }$
be a countable subset of
$D^{\lambda }_{\mu }$
be a countable subset of
![]() $I_{\mu }$
with
$I_{\mu }$
with
![]() $D^{\lambda }_{\mu } \cap \bigcup \left \lbrace D^{\alpha }_{\mu } \colon \alpha < \lambda \right \rbrace = R \cap I_{\mu }$
, and with
$D^{\lambda }_{\mu } \cap \bigcup \left \lbrace D^{\alpha }_{\mu } \colon \alpha < \lambda \right \rbrace = R \cap I_{\mu }$
, and with
![]() $|D^{\lambda }_{\mu } \setminus R| = |D^0_{\mu } \setminus R|$
. Some such set exists because
$|D^{\lambda }_{\mu } \setminus R| = |D^0_{\mu } \setminus R|$
. Some such set exists because
![]() $\left \lvert \bigcup \left \lbrace D^{\alpha }_{\mu } \colon \alpha < \lambda \right \rbrace \right \rvert = \lambda < \mu = |I_{\mu }|$
, so we may take
$\left \lvert \bigcup \left \lbrace D^{\alpha }_{\mu } \colon \alpha < \lambda \right \rbrace \right \rvert = \lambda < \mu = |I_{\mu }|$
, so we may take
![]() $D^{\lambda }_{\mu }$
to be any subset (of the appropriate size) of
$D^{\lambda }_{\mu }$
to be any subset (of the appropriate size) of
![]() $I_{\mu } \setminus \bigcup \left \lbrace D^{\alpha }_{\mu } \colon \alpha < \lambda \right \rbrace $
, together with
$I_{\mu } \setminus \bigcup \left \lbrace D^{\alpha }_{\mu } \colon \alpha < \lambda \right \rbrace $
, together with
![]() $R \cap I_{\mu }$
.
$R \cap I_{\mu }$
.
For each
![]() $\mu \in C$
, fix a bijection
$\mu \in C$
, fix a bijection
![]() $\phi ^{\lambda }_{\mu }: D^{\lambda }_{\mu } \to \omega $
such that
$\phi ^{\lambda }_{\mu }: D^{\lambda }_{\mu } \to \omega $
such that
![]() $\phi ^{\lambda }_{\mu } \!\restriction \! R = \phi ^0_{\mu } \!\restriction \! R$
. For each
$\phi ^{\lambda }_{\mu } \!\restriction \! R = \phi ^0_{\mu } \!\restriction \! R$
. For each
![]() $\alpha < \lambda $
and
$\alpha < \lambda $
and
![]() $\mu \in C$
, let
$\mu \in C$
, let
![]() $\phi ^{\alpha ,\lambda }_{\mu }$
and
$\phi ^{\alpha ,\lambda }_{\mu }$
and
![]() $\phi ^{\lambda ,\alpha }_{\mu }$
be the involutions of
$\phi ^{\lambda ,\alpha }_{\mu }$
be the involutions of
![]() $I_{\mu }$
defined just like the
$I_{\mu }$
defined just like the
![]() $\phi ^{\alpha ,\beta }_{\mu }$
above, but using
$\phi ^{\alpha ,\beta }_{\mu }$
above, but using
![]() $\phi ^{\lambda }_{\mu }$
in place of
$\phi ^{\lambda }_{\mu }$
in place of
![]() $\phi ^{\beta }_{\mu }$
. This naturally extends the system of involutions described above: for any
$\phi ^{\beta }_{\mu }$
. This naturally extends the system of involutions described above: for any
![]() $\alpha ,\beta \leq \lambda $
,
$\alpha ,\beta \leq \lambda $
,
-
∘
 $\phi ^{\alpha ,\beta }_{\mu }$
maps
$\phi ^{\alpha ,\beta }_{\mu }$
maps
 $D^{\alpha }_{\mu }$
onto
$D^{\alpha }_{\mu }$
onto
 $D^{\beta }_{\mu }$
and
$D^{\beta }_{\mu }$
and
 $D^{\beta }_{\mu }$
onto
$D^{\beta }_{\mu }$
onto
 $D^{\alpha }_{\mu }$
, but acts as the identity on the rest of
$D^{\alpha }_{\mu }$
, but acts as the identity on the rest of
 $I_{\mu }$
,
$I_{\mu }$
, -
∘ each
 $\phi ^{\alpha ,\beta }_{\mu }$
acts as the identity on
$\phi ^{\alpha ,\beta }_{\mu }$
acts as the identity on
 $R \cap I_{\mu }$
, and
$R \cap I_{\mu }$
, and -
∘
 $\phi ^{\alpha ,\beta }_{\mu } = \phi ^{\gamma ,\beta }_{\mu } \circ \phi ^{\alpha ,\gamma }_{\mu }$
for any
$\phi ^{\alpha ,\beta }_{\mu } = \phi ^{\gamma ,\beta }_{\mu } \circ \phi ^{\alpha ,\gamma }_{\mu }$
for any
 $\gamma \leq \lambda $
.
$\gamma \leq \lambda $
.
For each
![]() $\alpha ,\beta \leq \lambda $
, let
$\alpha ,\beta \leq \lambda $
, let
![]() $\phi ^{\alpha ,\beta } = \bigotimes _{\mu \in C}\phi ^{\alpha ,\beta }_{\mu }$
. By Lemma 3.11,
$\phi ^{\alpha ,\beta } = \bigotimes _{\mu \in C}\phi ^{\alpha ,\beta }_{\mu }$
. By Lemma 3.11,
![]() $\bar \phi ^{\alpha ,\beta } \!\restriction \! \mathbb {P}_{\kappa }$
is an automorphism of
$\bar \phi ^{\alpha ,\beta } \!\restriction \! \mathbb {P}_{\kappa }$
is an automorphism of
![]() $\mathbb {P}_{\kappa }$
for each
$\mathbb {P}_{\kappa }$
for each
![]() $\alpha ,\beta \leq \lambda $
.
$\alpha ,\beta \leq \lambda $
.
Because
![]() $\mathrm {hdom}_{\mu }(q) \subseteq R$
for all
$\mathrm {hdom}_{\mu }(q) \subseteq R$
for all
![]() $\mu $
and
$\mu $
and
![]() $\phi ^{0,\lambda }$
fixes R,
$\phi ^{0,\lambda }$
fixes R,
![]() $\bar \phi ^{0,\lambda }(q) = q$
. Recall
$\bar \phi ^{0,\lambda }(q) = q$
. Recall
Applying standard facts about automorphisms of forcing posets,
Let
![]() $B_{\lambda }$
denote the evaluation of
$B_{\lambda }$
denote the evaluation of
![]() $\dot B_{\lambda }$
in
$\dot B_{\lambda }$
in
![]() $V^{\mathbb {P}_{\kappa }}$
, and let
$V^{\mathbb {P}_{\kappa }}$
, and let
![]() $\tilde B_{\lambda }$
be the Borel set that it codes. So, in particular, the displayed statement above implies that
$\tilde B_{\lambda }$
be the Borel set that it codes. So, in particular, the displayed statement above implies that
![]() $q = \bar \phi ^{0,\lambda }(q) \Vdash \tilde B_{\lambda } \neq \emptyset $
. To show
$q = \bar \phi ^{0,\lambda }(q) \Vdash \tilde B_{\lambda } \neq \emptyset $
. To show
![]() $q \Vdash \bigcup _{\alpha < \lambda }\tilde B_{\alpha } \neq \mathbb {R}$
, it now suffices to show
$q \Vdash \bigcup _{\alpha < \lambda }\tilde B_{\alpha } \neq \mathbb {R}$
, it now suffices to show
![]() $q \Vdash \tilde B_{\lambda } \cap \tilde B_{\beta } = \emptyset $
for all
$q \Vdash \tilde B_{\lambda } \cap \tilde B_{\beta } = \emptyset $
for all
![]() $\beta < \lambda $
.
$\beta < \lambda $
.
Fix
![]() $\beta < \lambda $
. By our choice of the sets
$\beta < \lambda $
. By our choice of the sets
![]() $D^{\lambda }_{\mu }$
, we have
$D^{\lambda }_{\mu }$
, we have
![]() $D^{\lambda }_{\mu } \cap D^{\beta }_{\mu } \subseteq R$
for all
$D^{\lambda }_{\mu } \cap D^{\beta }_{\mu } \subseteq R$
for all
![]() $\mu \in C$
, and therefore
$\mu \in C$
, and therefore
![]() $D^{\lambda } \cap D^{\beta } \subseteq R$
. Because
$D^{\lambda } \cap D^{\beta } \subseteq R$
. Because
![]() $\left \lbrace D^{\alpha } \colon \alpha \in \mathcal {A}_2 \right \rbrace $
is a
$\left \lbrace D^{\alpha } \colon \alpha \in \mathcal {A}_2 \right \rbrace $
is a
![]() $\Delta $
-system of size
$\Delta $
-system of size
![]() $\nu $
, and because
$\nu $
, and because
![]() $|D^{\beta }| \leq |C| \cdot \aleph _0 < \kappa < \nu $
, there is some
$|D^{\beta }| \leq |C| \cdot \aleph _0 < \kappa < \nu $
, there is some
![]() $\alpha \in \mathcal {A}_2$
with
$\alpha \in \mathcal {A}_2$
with
![]() $D^{\alpha } \cap D^{\beta } \subseteq R$
(regardless of whether
$D^{\alpha } \cap D^{\beta } \subseteq R$
(regardless of whether
![]() $\beta \in \mathcal {A}_2$
). Fix some such
$\beta \in \mathcal {A}_2$
). Fix some such
![]() $\alpha $
.
$\alpha $
.
Note that
![]() $\phi ^{\alpha ,\lambda }$
sends
$\phi ^{\alpha ,\lambda }$
sends
![]() $D^{\alpha }$
to
$D^{\alpha }$
to
![]() $D^{\lambda }$
, while acting as the identity on
$D^{\lambda }$
, while acting as the identity on
![]() $D^{\beta }$
. And because
$D^{\beta }$
. And because
![]() $0,\alpha \in \mathcal {A}_2$
, our choice of
$0,\alpha \in \mathcal {A}_2$
, our choice of
![]() $\mathcal {A}_2$
implies
$\mathcal {A}_2$
implies
![]() $\bar \phi ^{0,\alpha }(\dot B_0) = \dot B_{\alpha }$
. It follows that
$\bar \phi ^{0,\alpha }(\dot B_0) = \dot B_{\alpha }$
. It follows that
while
![]() $\bar \phi ^{\alpha ,\lambda }(\dot B_{\beta }) = \dot B_{\beta }$
. But
$\bar \phi ^{\alpha ,\lambda }(\dot B_{\beta }) = \dot B_{\beta }$
. But
Applying the automorphism
![]() $\bar \phi ^{\alpha ,\lambda }$
of
$\bar \phi ^{\alpha ,\lambda }$
of
![]() $\mathbb {P}_{\kappa }$
,
$\mathbb {P}_{\kappa }$
,
Because
![]() $\beta $
was arbitrary, this shows that
$\beta $
was arbitrary, this shows that
![]() $q \Vdash \tilde B_{\lambda } \cap \tilde B_{\beta } = \emptyset $
for all
$q \Vdash \tilde B_{\lambda } \cap \tilde B_{\beta } = \emptyset $
for all
![]() $\beta < \lambda $
. In other words,
$\beta < \lambda $
. In other words,
![]() $q \Vdash \bigcup _{\alpha < \lambda }\tilde B_{\alpha } \neq \mathbb {R}$
.
$q \Vdash \bigcup _{\alpha < \lambda }\tilde B_{\alpha } \neq \mathbb {R}$
.
Note that Theorem 3.2 only gives us models in which
![]() $\acute {\mathfrak {n}}$
is regular and
$\acute {\mathfrak {n}}$
is regular and
![]() $|\mathfrak {sp}({\small\text{closed}})| \leq \acute {\mathfrak {n}}$
. Both of these are merely artifacts of the proof: neither need be true of
$|\mathfrak {sp}({\small\text{closed}})| \leq \acute {\mathfrak {n}}$
. Both of these are merely artifacts of the proof: neither need be true of
![]() $\mathfrak {sp}({\small\text{closed}})$
in general. As mentioned near the end of Section 2, it is possible that
$\mathfrak {sp}({\small\text{closed}})$
in general. As mentioned near the end of Section 2, it is possible that
![]() ${\mathfrak d} = \mathfrak {c} = \kappa $
for some singular cardinal
${\mathfrak d} = \mathfrak {c} = \kappa $
for some singular cardinal
![]() $\kappa $
of uncountable cofinality, and this makes
$\kappa $
of uncountable cofinality, and this makes
![]() $\acute {\mathfrak {n}} = \kappa $
also. And of course, Theorem 3.1 shows it is possible to have
$\acute {\mathfrak {n}} = \kappa $
also. And of course, Theorem 3.1 shows it is possible to have
![]() $|\mathfrak {sp}({\small\text{closed}})|> \acute {\mathfrak {n}}$
.
$|\mathfrak {sp}({\small\text{closed}})|> \acute {\mathfrak {n}}$
.
Theorem 3.2 also cannot produce a model in which
![]() $\mathfrak {sp}({\small\text{closed}}) \cap \kappa $
is unbounded for a regular limit cardinal
$\mathfrak {sp}({\small\text{closed}}) \cap \kappa $
is unbounded for a regular limit cardinal
![]() $\kappa $
. Theorem 3.1 implies that this is possible, but in such a case automatically gives
$\kappa $
. Theorem 3.1 implies that this is possible, but in such a case automatically gives
![]() $\kappa \in \mathfrak {sp}({\small\text{closed}})$
. This suggests the following question:
$\kappa \in \mathfrak {sp}({\small\text{closed}})$
. This suggests the following question:
Question 3.13.
Is
![]() $\mathfrak {sp}({\small\text{closed}})$
or
$\mathfrak {sp}({\small\text{closed}})$
or
![]() $\mathfrak {sp}({\small\text{Borel}})$
closed under regular limits?
$\mathfrak {sp}({\small\text{Borel}})$
closed under regular limits?
We also do not know whether our final condition on C is an artifact of the proof.
Question 3.14.
Is it consistent that
![]() $\aleph _{\omega } \in \mathfrak {sp}({\small\text{closed}})$
but
$\aleph _{\omega } \in \mathfrak {sp}({\small\text{closed}})$
but
![]() $\aleph _{\omega +1} \notin \mathfrak {sp}({\small\text{closed}})$
? What about
$\aleph _{\omega +1} \notin \mathfrak {sp}({\small\text{closed}})$
? What about
![]() $\mathfrak {sp}({\small\text{Borel}})$
?
$\mathfrak {sp}({\small\text{Borel}})$
?
For any pointclass
![]() $\Gamma $
, define
$\Gamma $
, define
To strengthen Theorem 3.2, we could replace
![]() $\mathfrak {sp}({\small\text{Borel}})$
in the conclusion of the theorem with
$\mathfrak {sp}({\small\text{Borel}})$
in the conclusion of the theorem with
![]() $\mathfrak {sp}({\scriptstyle\text{\(\Gamma\)}})$
for some pointclass
$\mathfrak {sp}({\scriptstyle\text{\(\Gamma\)}})$
for some pointclass
![]() $\Gamma $
strictly containing the Borel sets. The ultimate result in this direction would be to take
$\Gamma $
strictly containing the Borel sets. The ultimate result in this direction would be to take
![]() $\Gamma = \text {OD}(\mathbb {R})$
, since this is essentially the largest pointclass of interest from a descriptive point of view.
$\Gamma = \text {OD}(\mathbb {R})$
, since this is essentially the largest pointclass of interest from a descriptive point of view.
While we have chosen to focus on
![]() $\mathfrak {sp}({\small\text{Borel}})$
and
$\mathfrak {sp}({\small\text{Borel}})$
and
![]() $\mathfrak {sp}({\small\text{closed}})$
until now, let us observe that minor modifications to the proof of Theorem 3.2 will give a proof of the stronger version, where
$\mathfrak {sp}({\small\text{closed}})$
until now, let us observe that minor modifications to the proof of Theorem 3.2 will give a proof of the stronger version, where
![]() $\mathfrak {sp}({\small\text{Borel}})$
is replaced by
$\mathfrak {sp}({\small\text{Borel}})$
is replaced by
![]() $\mathfrak {sp}({\scriptstyle\text{OD(\(\mathbb {R}\))}})$
in the conclusion. Consequently, Corollaries 3.4 and 3.5 can also be strengthened by replacing
$\mathfrak {sp}({\scriptstyle\text{OD(\(\mathbb {R}\))}})$
in the conclusion. Consequently, Corollaries 3.4 and 3.5 can also be strengthened by replacing
![]() $\mathfrak {sp}({\small\text{Borel}})$
with
$\mathfrak {sp}({\small\text{Borel}})$
with
![]() $\mathfrak {sp}({\scriptstyle\text{OD(\(\mathbb {R}\))}})$
. This has the interesting consequence that large cardinals do not imply the existence of a partition of
$\mathfrak {sp}({\scriptstyle\text{OD(\(\mathbb {R}\))}})$
. This has the interesting consequence that large cardinals do not imply the existence of a partition of
![]() $\mathbb {R}$
into
$\mathbb {R}$
into
![]() $\aleph _2$
projective sets. This consequence is already known, by the work of Blass [Reference Blass and Judah2] mentioned at the start of this section.
$\aleph _2$
projective sets. This consequence is already known, by the work of Blass [Reference Blass and Judah2] mentioned at the start of this section.
We close with three more open questions.
Question 3.15.
Is
![]() $\mathfrak {sp}({\small\text{Borel}}) = \mathfrak {sp}({\scriptstyle\text{OD(\(\mathbb {R}\))}})$
?
$\mathfrak {sp}({\small\text{Borel}}) = \mathfrak {sp}({\scriptstyle\text{OD(\(\mathbb {R}\))}})$
?
Question 3.16. Given
![]() $\alpha < \omega _1$
, is it consistent that
$\alpha < \omega _1$
, is it consistent that
![]() $\mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{\alpha}\)}}) \neq \mathfrak {sp}({\small\text{\(\mathbf {\Pi}^{0}_{\alpha +1}\)}})$
?
$\mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{\alpha}\)}}) \neq \mathfrak {sp}({\small\text{\(\mathbf {\Pi}^{0}_{\alpha +1}\)}})$
?
The answer to this question is currently known for
![]() $\alpha = 1,2$
. For
$\alpha = 1,2$
. For
![]() $\alpha =1$
, Miller proved the consistency of
$\alpha =1$
, Miller proved the consistency of
![]() $\mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{1}\)}}) \neq \mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{2}\)}})$
(i.e.,
$\mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{1}\)}}) \neq \mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{2}\)}})$
(i.e.,
![]() $\mathfrak {sp}({\small\text{closed}}) \neq \mathfrak {sp}({\small\text{\(G_{\delta}\)}})$
) by constructing a model with
$\mathfrak {sp}({\small\text{closed}}) \neq \mathfrak {sp}({\small\text{\(G_{\delta}\)}})$
) by constructing a model with
![]() $\aleph _1 = \mathrm {cov}(\mathcal M) < \acute {\mathfrak {n}}$
[Reference Miller, Barwise, Keisler and Kunen17, Theorem 5]. This shows
$\aleph _1 = \mathrm {cov}(\mathcal M) < \acute {\mathfrak {n}}$
[Reference Miller, Barwise, Keisler and Kunen17, Theorem 5]. This shows
![]() $\mathfrak {sp}({\small\text{closed}}) \neq \mathfrak {sp}({\small\text{\(G_{\delta}\)}})$
, because if
$\mathfrak {sp}({\small\text{closed}}) \neq \mathfrak {sp}({\small\text{\(G_{\delta}\)}})$
, because if
![]() $\aleph _1 = \mathrm {cov}(\mathcal M)$
, then
$\aleph _1 = \mathrm {cov}(\mathcal M)$
, then
![]() $\aleph _1 \in \mathfrak {sp}({\small\text{\(G_{\delta}\)}})$
. (Proof: if
$\aleph _1 \in \mathfrak {sp}({\small\text{\(G_{\delta}\)}})$
. (Proof: if
![]() $\left \lbrace F_{\alpha } \colon \alpha < \omega _1 \right \rbrace $
is a collection of closed nowhere dense sets covering
$\left \lbrace F_{\alpha } \colon \alpha < \omega _1 \right \rbrace $
is a collection of closed nowhere dense sets covering
![]() $\mathbb {R}$
, then
$\mathbb {R}$
, then
![]() $\{ F_{\alpha } \setminus \bigcup _{\xi < \alpha } :\, \alpha < \omega _1 \}$
is a partition of
$\{ F_{\alpha } \setminus \bigcup _{\xi < \alpha } :\, \alpha < \omega _1 \}$
is a partition of
![]() $\mathbb {R}$
into
$\mathbb {R}$
into
![]() $G_{\delta }$
sets.) For
$G_{\delta }$
sets.) For
![]() $\alpha = 2$
, the consistency of
$\alpha = 2$
, the consistency of
![]() $\mathfrak {sp}({\small\text{\(\mathbf {\Pi}^{0}_{2}\)}}) \neq \mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{3}\)}})$
(i.e.,
$\mathfrak {sp}({\small\text{\(\mathbf {\Pi}^{0}_{2}\)}}) \neq \mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{3}\)}})$
(i.e.,
![]() $\mathfrak {sp}({\small\text{\(G_{\delta}\)}}) \neq \mathfrak {sp}({\small\text{\(F_{\sigma \delta}\)}})$
) follows from Hausdorff’s theorem that
$\mathfrak {sp}({\small\text{\(G_{\delta}\)}}) \neq \mathfrak {sp}({\small\text{\(F_{\sigma \delta}\)}})$
) follows from Hausdorff’s theorem that
![]() $\aleph _1 \in \mathfrak {sp}({\small\text{\(\mathbf {\Pi }^0_3\)}})$
, together with a result of Fremlin and Shelah [Reference Fremlin and Shelah9] stating that
$\aleph _1 \in \mathfrak {sp}({\small\text{\(\mathbf {\Pi }^0_3\)}})$
, together with a result of Fremlin and Shelah [Reference Fremlin and Shelah9] stating that
![]() $\min \!\big ( \mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{2}\)}}) \big ) \geq \mathrm {cov}(\mathcal M)$
.
$\min \!\big ( \mathfrak {sp}({\small\text{\(\mathbf {\Pi }^{0}_{2}\)}}) \big ) \geq \mathrm {cov}(\mathcal M)$
.
Question 3.17.
Is it consistent that
![]() $\mathfrak {sp}({\small\text{closed}}) \neq \mathfrak {sp}({\small\text{\(G_{\delta}\)}})$
and
$\mathfrak {sp}({\small\text{closed}}) \neq \mathfrak {sp}({\small\text{\(G_{\delta}\)}})$
and
![]() $\mathrm {cov}(\mathcal M)> \aleph _1$
?
$\mathrm {cov}(\mathcal M)> \aleph _1$
?