Partitions of products

Extract

We will consider some partition properties of the following type: given a function F: ω^ω →2, is there a sequence H₀, H₁, … of subsets of ω such that F is constant on Π_iεωH_i? The answer is obviously positive if we allow all the H_i's to have exactly one element, but the problem is nontrivial if we require the H_i's to have at least two elements. The axiom of choice contradicts the statement “for all F: ω^ω→ 2 there is a sequence H₀, H₁, H₂,… of subsets of ω such that {i|(H_i) ≥ 2} is infinite and F is constant on ΠH_i”, but the infinite exponent partition relation ω(ω)^ω implies it; so, this statement is relatively consistent with an inaccessible cardinal. (See [1] where these partition properties were considered.)

We will also consider partitions into any finite number of pieces, and we will prove some facts about partitions into ω-many pieces.

Given a partition F: ω^ω → k, we say that H₀, H₁…, a sequence of subsets of ω, is homogeneous for F if F is constant on ΠH_i. We say the sequence H₀, H₁,… is nonoverlapping if, for all i ∈ ω, ∪H_i > ∩H_i+1.

The sequence 〈H_i: i ∈ ω〉 is of type 〈α₀, α₁,…〉 if, for every i ∈ ω, ∣H_i∣ = α_i.

We will adopt the usual notation for polarized partition relations due to Erdös, Hajnal, and Rado.

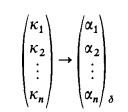
means that for every partition F: κ₁ × κ₂ × … × κ_n→δ there is a sequence H₀, H₁,…, H_n such that H_i ⊂ κ_i and ∣H_i∣ = α_i for every i, 1 ≤ i ≤ n, and F is constant on H₁ × H₂ × … × H_n.