Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T01:29:09.877Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomially and superexponentially shorter proofs in fragments of arithmetic

Published online by Cambridge University Press:  12 March 2014

Franco Montagna
Franco Montagna*
Affiliation:
Scuola di Specializzione in Logica Matematica, Università di Siena, 53100 Siena, Italy, E-mail: montagna@sivax.cineca.it
Get access Rights & Permissions [Opens in a new window]

Extract

In Parikh [71] it is shown that, if T is an r.e. consistent extension of Peano arithmetic PA, then, for each primitive recursive function g, there is a formula φ of PA such that

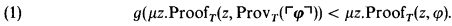
(In the following, Proof T(z, φ) and Prov T(φ) denote the metalinguistic assertions that z codes a proof of φ in T and that φ is provable in T respectively, where ProofT(z, ┌φ┐) and ProvT(┌φ┐) are the formalizations of Proof T(z,φ) and ProvT(φ) respectively in the language of PA, ┌φ┐ denotes the Gödel number of φ and ┌φ┐ denotes the corresponding numeral. Also, for typographical reasons, subscripts will not be made boldface.) If g is a rapidly increasing function, we express (1) by saying that ProvT(┌φ┐) has a much shorter proof modulo g than φ. Parikh's result is based on the fact that a suitable formula A(x), roughly asserting that (1) holds with x in place of φ, has only provable fixed points. In de Jongh and Montagna [89], this situation is generalized and investigated in a modal context. There, a characterization is given of arithmetical formulas arising from modal formulas of a suitable modal language which have only provable fixed points, and Parikh's result is obtained as a particular case.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 3 , September 1992 , pp. 844 - 863
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bennett, J. H. [62], On spectra, Ph.D. thesis, Princeton University, Princeton, New Jersey.Google Scholar
Buss, S. [86], Bounded arithmetic, Bibliopolis, Napoli.Google Scholar
Carbone, A. [ta], Provable fixed points in I⊿0 + Ω1, preprint, University of Amsterdam, Amsterdam, 1990.Google Scholar
de Jongh, D. H. J. and Montagna, F. [88], Provable fixed points, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 34, pp. 229–250.CrossRefGoogle Scholar
de Jongh, D. H. J. and Montagna, F. [89], Much shorter proofs, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 35, pp. 247–260.CrossRefGoogle Scholar
de Jongh, D. H. J., Jumelet, M. and Montagna, F. [ta], On the proof of Solovay's theorem, Studia Logica (to appear).Google Scholar
Gaifman, H. and Dimitracopoulos, C. [82], Fragments of Peano arithmetic and the MRDP theorem, Logic and algorithmic, Monographies de l'Enseignement Mathématique, vol. 30, Université de Genève, Genève, pp. 319–329.Google Scholar
Guaspari, D. and Solovav, R. M. [79], Rosser sentences, Annals of Mathematical Logic, vol. 16, pp. 81–99.CrossRefGoogle Scholar
Krajíček, J. [89], On the number of steps in proofs, Annals of Pure and Applied Logic, vol. 41, pp. 153–178.CrossRefGoogle Scholar
Mostowski, A. [52], Sentences undecidable in formalized arithmetic: an exposition of the theory of Kurt Gödel, North-Holland, Amsterdam.Google Scholar
Parikh, R. [71], Existence and feasibility in arithmetic, this Journal, vol. 36, pp. 494–508.Google Scholar
Parikh, R. [73], Some results on the length of proofs, Transactions of the American Mathematical Society, vol. 177, pp. 29–36.CrossRefGoogle Scholar
Sambin, G. and Valentini, S. [82], The modal logic of provability: the sequential approach, Journal of Philosophical Logic, vol. 11, pp. 311–342.CrossRefGoogle Scholar
Smoryński, C. [85], Self-reference and modal logic, Springer-Verlag, Berlin.Google Scholar
Solovay, R. M. [76], Provability interpretations of modal logic, Israel Journal of Mathematics, vol. 25, pp. 287–304.CrossRefGoogle Scholar
Verbrugge, L. C. [88], Does Solovay's completeness theorem extend to bounded arithmetic, Master's thesis, University of Amsterdam, Amsterdam.Google Scholar
Verbrugge, L. C. [ta], Σ-completeness and bounded arithmetic, preprint, University of Amsterdam, Amsterdam, 1989.Google Scholar
Visser, A. [90], Interpretability logic, Mathematical logic: proceedings of the Heyting “88 summer school, Plenum Press, New York, pp. 175–209.Google Scholar
Visser, A. [92], An inside view of EXP, this Journal, vol. 57, pp. 130–165.Google Scholar
Visser, A. [ta], On the Σ1-conservativity of Σ1completeness, preprint, University of Utrecht, Utrecht, 1989.Google Scholar
Wilkie, A. J. and Paris, J. B. [87], On the scheme of induction for bounded arithmetical formulae, Annals of Pure and Applied Logic, vol. 35, pp. 261–302.CrossRefGoogle Scholar